$\mathcal{L}_1$Quad: $\mathcal{L}_1$ Adaptive Augmentation of Geometric Control for Agile Quadrotors with Performance Guarantees

Quadrotors that can operate safely in the presence of imperfect model knowledge and external disturbances are crucial in safety-critical applications. We present L1Quad, a control architecture for quadrotors based on the L1 adaptive control. L1Quad enables safe tubes centered around a desired trajectory that the quadrotor is always guaranteed to remain inside. Our design applies to both the rotational and the translational dynamics of the quadrotor. We lump various types of uncertainties and disturbances as unknown nonlinear (time- and state-dependent) forces and moments. Without assuming or enforcing parametric structures, L1Quad can accurately estimate and compensate for these unknown forces and moments. Extensive experimental results demonstrate that L1Quad is able to significantly outperform baseline controllers under a variety of uncertainties with consistently small tracking errors.

Geometric Tracking Control of Omnidirectional Multirotors in the Presence of Rotor Dynamics

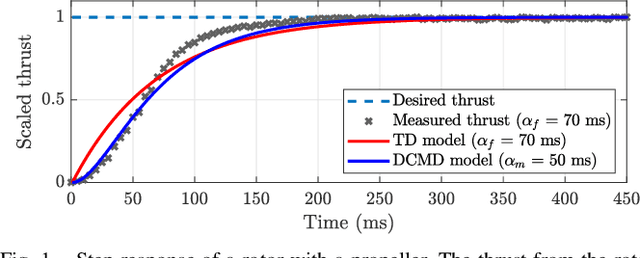
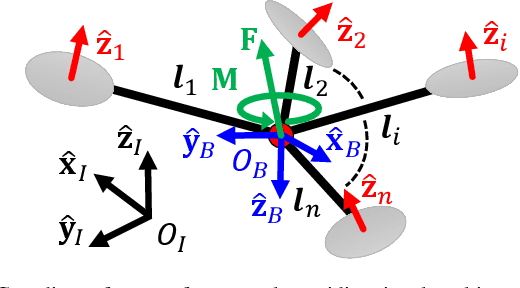
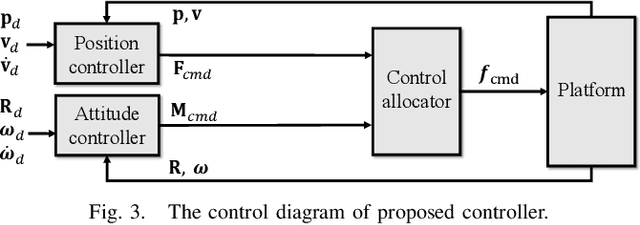
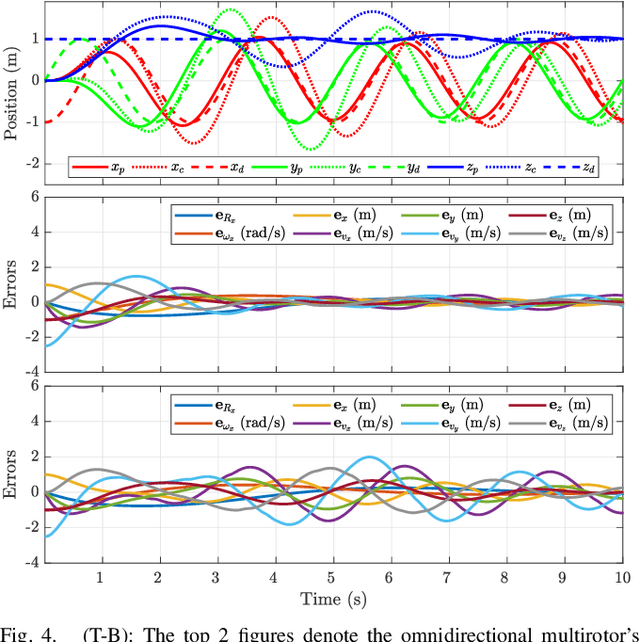
An omnidirectional multirotor has the advantageous maneuverability of decoupled translational and rotational motions, drastically superseding the traditional multirotors' motion capability. Such maneuverability requires an omnidirectional multirotor to frequently alter the thrust amplitude and even direction, which is prone to the rotors' settling time induced from the rotors' own dynamics. Furthermore, the omnidirectional multirotor's stability for tracking control in the presence of rotor dynamics has not yet been addressed. To resolve this issue, we propose a geometric tracking controller that takes the rotor dynamics into account. We show that the proposed controller yields the zero equilibrium of the error dynamics almost globally exponentially stable. The controller's tracking performance and stability are verified in simulations. Furthermore, the single-axis force experiment with the omnidirectional multirotor has been performed to confirm the proposed controller's performance in mitigating the rotors' settling time in the real world.

DiffTune: Auto-Tuning through Auto-Differentiation

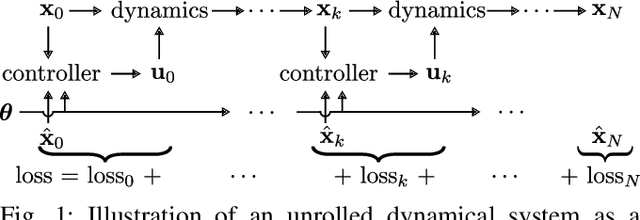
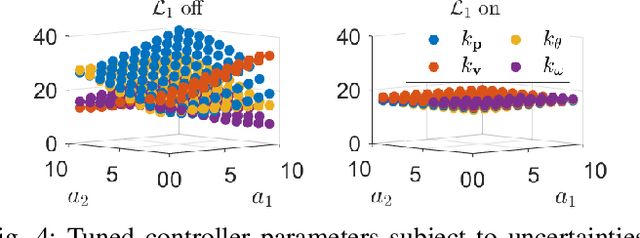
The performance of a robot controller depends on the choice of its parameters, which require careful tuning. In this paper, we present DiffTune, a novel, gradient-based automatic tuning framework. Our method unrolls the dynamical system and controller as a computational graph and updates the controller parameters through gradient-based optimization. Unlike the commonly used back-propagation scheme, the gradient in DiffTune is obtained through sensitivity propagation, a forward-mode auto differentiation technique that runs parallel to the system's evolution. We validate the proposed auto-tune approach on a Dubin's car and a quadrotor in challenging simulation environments. Simulation experiments show that the approach is robust to uncertainties in the system dynamics and environment and generalizes well to unseen trajectories in tuning.

$\mathcal{RL}_1$-$\mathcal{GP}$: Safe Simultaneous Learning and Control

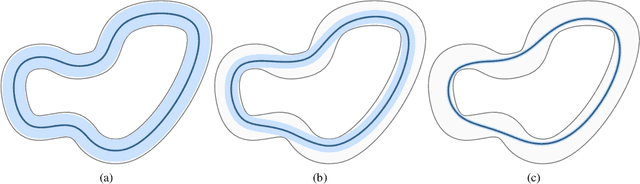
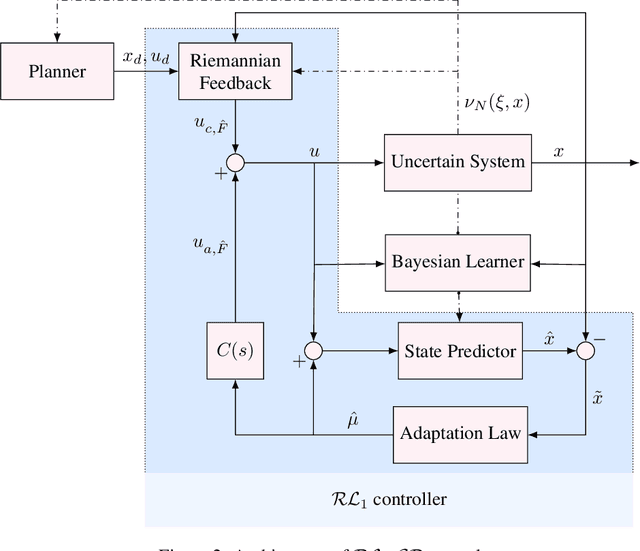
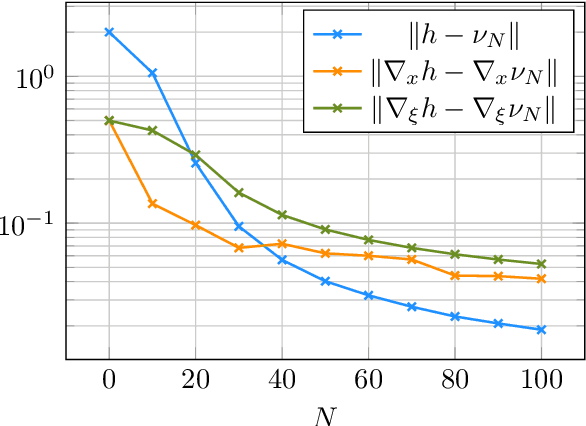
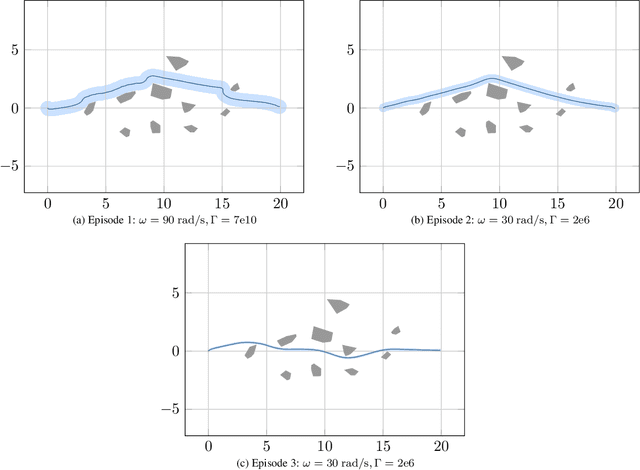
We present $\mathcal{RL}_1$-$\mathcal{GP}$, a control framework that enables safe simultaneous learning and control for systems subject to uncertainties. The two main constituents are Riemannian energy $\mathcal{L}_1$ ($\mathcal{RL}_1$) control and Bayesian learning in the form of Gaussian process (GP) regression. The $\mathcal{RL}_1$ controller ensures that control objectives are met while providing safety certificates. Furthermore, $\mathcal{RL}_1$-$\mathcal{GP}$ incorporates any available data into a GP model of uncertainties, which improves performance and enables the motion planner to achieve optimality safely. This way, the safe operation of the system is always guaranteed, even during the learning transients. We provide a few illustrative examples for the safe learning and control of planar quadrotor systems in a variety of environments.