Robust Model Based Reinforcement Learning Using $\mathcal{L}_1$ Adaptive Control
Paper and Code
Mar 21, 2024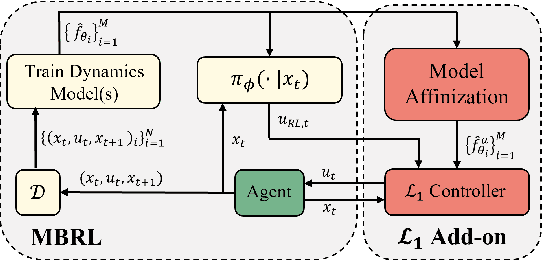
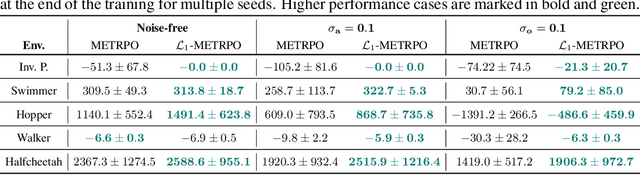
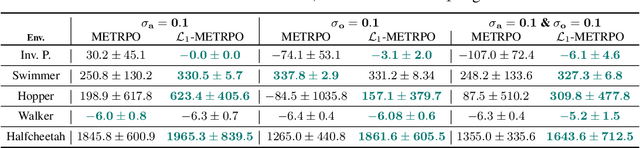
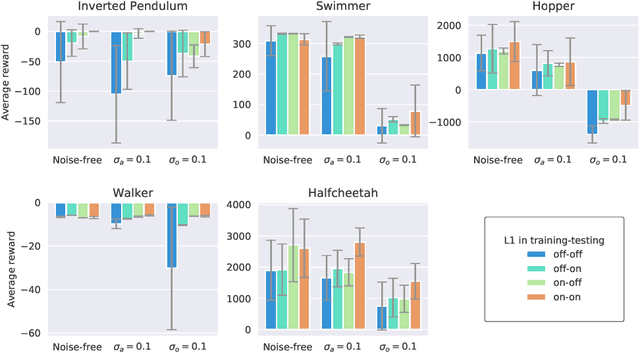
We introduce $\mathcal{L}_1$-MBRL, a control-theoretic augmentation scheme for Model-Based Reinforcement Learning (MBRL) algorithms. Unlike model-free approaches, MBRL algorithms learn a model of the transition function using data and use it to design a control input. Our approach generates a series of approximate control-affine models of the learned transition function according to the proposed switching law. Using the approximate model, control input produced by the underlying MBRL is perturbed by the $\mathcal{L}_1$ adaptive control, which is designed to enhance the robustness of the system against uncertainties. Importantly, this approach is agnostic to the choice of MBRL algorithm, enabling the use of the scheme with various MBRL algorithms. MBRL algorithms with $\mathcal{L}_1$ augmentation exhibit enhanced performance and sample efficiency across multiple MuJoCo environments, outperforming the original MBRL algorithms, both with and without system noise.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge