A review of path following control strategies for autonomous robotic vehicles: theory, simulations, and experiments

This article presents an in-depth review of the topic of path following for autonomous robotic vehicles, with a specific focus on vehicle motion in two dimensional space (2D). From a control system standpoint, path following can be formulated as the problem of stabilizing a path following error system that describes the dynamics of position and possibly orientation errors of a vehicle with respect to a path, with the errors defined in an appropriate reference frame. In spite of the large variety of path following methods described in the literature we show that, in principle, most of them can be categorized in two groups: stabilization of the path following error system expressed either in the vehicle's body frame or in a frame attached to a "reference point" moving along the path, such as a Frenet-Serret (F-S) frame or a Parallel Transport (P-T) frame. With this observation, we provide a unified formulation that is simple but general enough to cover many methods available in the literature. We then discuss the advantages and disadvantages of each method, comparing them from the design and implementation standpoint. We further show experimental results of the path following methods obtained from field trials testing with under-actuated and fully-actuated autonomous marine vehicles. In addition, we introduce open-source Matlab and Gazebo/ROS simulation toolboxes that are helpful in testing path following methods prior to their integration in the combined guidance, navigation, and control systems of autonomous vehicles.

Bernstein approximation of optimal control problems

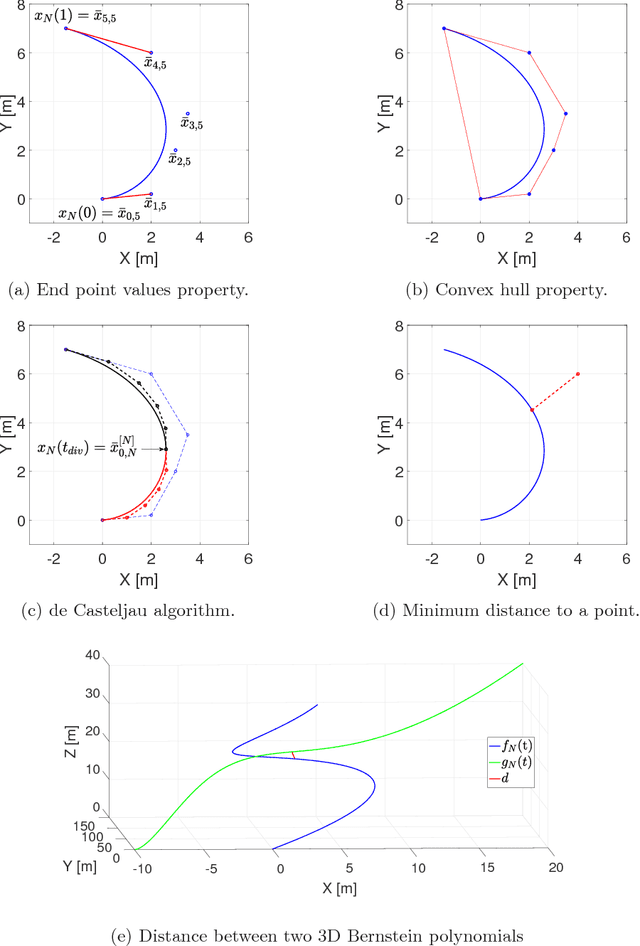
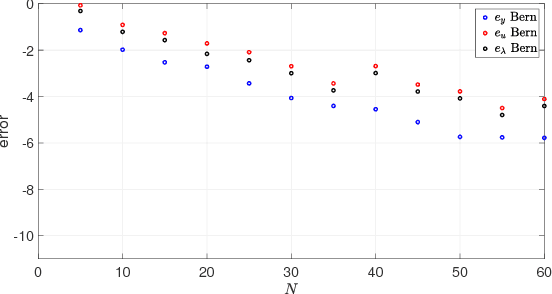
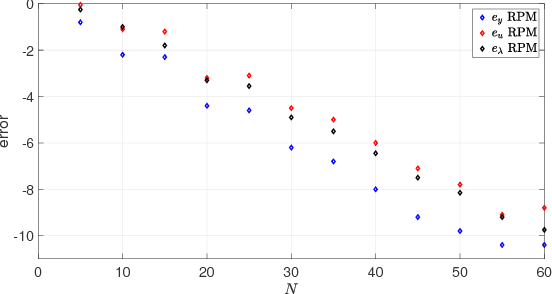
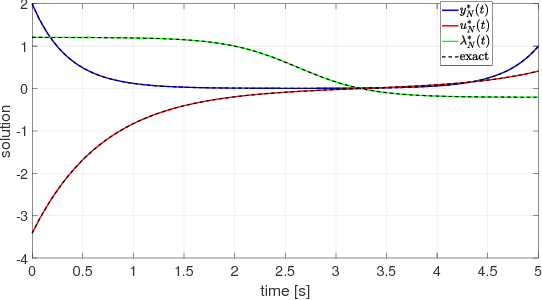
Bernstein polynomial approximation to a continuous function has a slower rate of convergence as compared to other approximation methods. "The fact seems to have precluded any numerical application of Bernstein polynomials from having been made. Perhaps they will find application when the properties of the approximant in the large are of more importance than the closeness of the approximation." -- has remarked P.J. Davis in his 1963 book Interpolation and Approximation. This paper presents a direct approximation method for nonlinear optimal control problems with mixed input and state constraints based on Bernstein polynomial approximation. We provide a rigorous analysis showing that the proposed method yields consistent approximations of time continuous optimal control problems. Furthermore, we demonstrate that the proposed method can also be used for costate estimation of the optimal control problems. This latter result leads to the formulation of the Covector Mapping Theorem for Bernstein polynomial approximation. Finally, we explore the numerical and geometric properties of Bernstein polynomials, and illustrate the advantages of the proposed approximation method through several numerical examples.