Swarm Characteristic Classification using Robust Neural Networks with Optimized Controllable Inputs

Having the ability to infer characteristics of autonomous agents would profoundly revolutionize defense, security, and civil applications. Our previous work was the first to demonstrate that supervised neural network time series classification (NN TSC) could rapidly predict the tactics of swarming autonomous agents in military contexts, providing intelligence to inform counter-maneuvers. However, most autonomous interactions, especially military engagements, are fraught with uncertainty, raising questions about the practicality of using a pretrained classifier. This article addresses that challenge by leveraging expected operational variations to construct a richer dataset, resulting in a more robust NN with improved inference performance in scenarios characterized by significant uncertainties. Specifically, diverse datasets are created by simulating variations in defender numbers, defender motions, and measurement noise levels. Key findings indicate that robust NNs trained on an enriched dataset exhibit enhanced classification accuracy and offer operational flexibility, such as reducing resources required and offering adherence to trajectory constraints. Furthermore, we present a new framework for optimally deploying a trained NN by the defenders. The framework involves optimizing defender trajectories that elicit adversary responses that maximize the probability of correct NN tactic classification while also satisfying operational constraints imposed on the defenders.

Swarm Characteristics Classification Using Neural Networks

Understanding the characteristics of swarming autonomous agents is critical for defense and security applications. This article presents a study on using supervised neural network time series classification (NN TSC) to predict key attributes and tactics of swarming autonomous agents for military contexts. Specifically, NN TSC is applied to infer two binary attributes - communication and proportional navigation - which combine to define four mutually exclusive swarm tactics. We identify a gap in literature on using NNs for swarm classification and demonstrate the effectiveness of NN TSC in rapidly deducing intelligence about attacking swarms to inform counter-maneuvers. Through simulated swarm-vs-swarm engagements, we evaluate NN TSC performance in terms of observation window requirements, noise robustness, and scalability to swarm size. Key findings show NNs can predict swarm behaviors with 97% accuracy using short observation windows of 20 time steps, while also demonstrating graceful degradation down to 80% accuracy under 50% noise, as well as excellent scalability to swarm sizes from 10 to 100 agents. These capabilities are promising for real-time decision-making support in defense scenarios by rapidly inferring insights about swarm behavior.

Bernstein approximation of optimal control problems

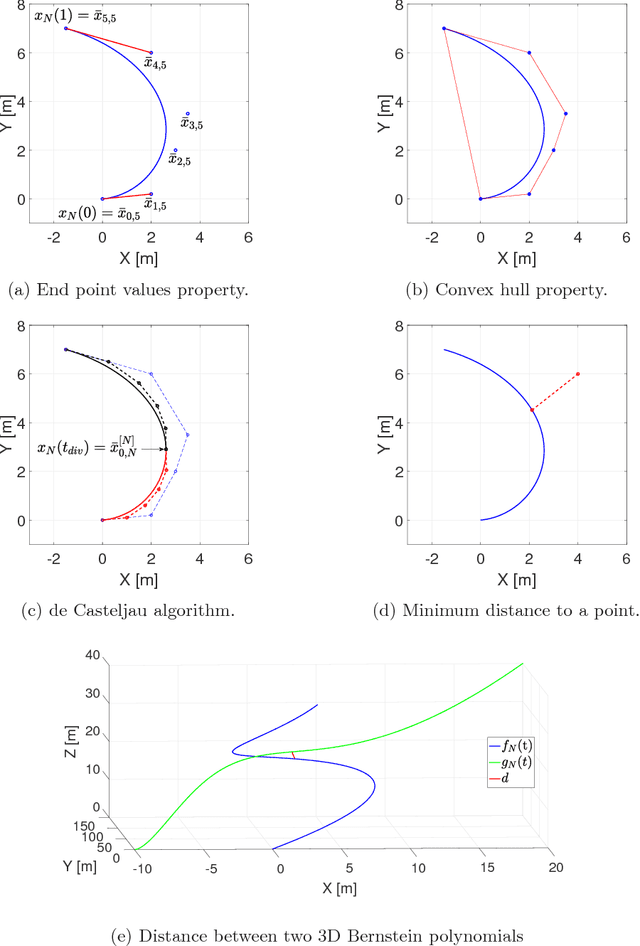
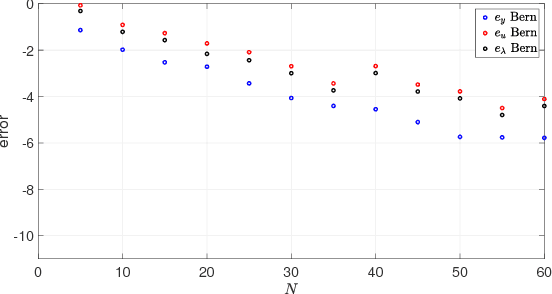
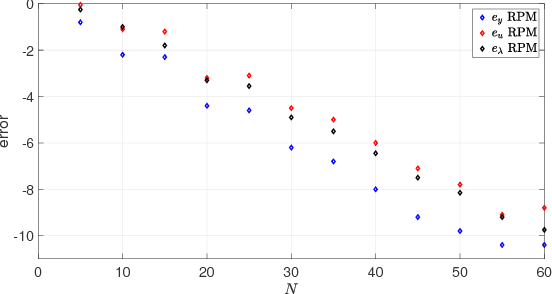
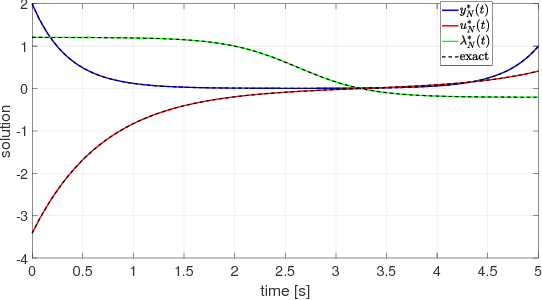
Bernstein polynomial approximation to a continuous function has a slower rate of convergence as compared to other approximation methods. "The fact seems to have precluded any numerical application of Bernstein polynomials from having been made. Perhaps they will find application when the properties of the approximant in the large are of more importance than the closeness of the approximation." -- has remarked P.J. Davis in his 1963 book Interpolation and Approximation. This paper presents a direct approximation method for nonlinear optimal control problems with mixed input and state constraints based on Bernstein polynomial approximation. We provide a rigorous analysis showing that the proposed method yields consistent approximations of time continuous optimal control problems. Furthermore, we demonstrate that the proposed method can also be used for costate estimation of the optimal control problems. This latter result leads to the formulation of the Covector Mapping Theorem for Bernstein polynomial approximation. Finally, we explore the numerical and geometric properties of Bernstein polynomials, and illustrate the advantages of the proposed approximation method through several numerical examples.