Biologically Inspired Collision Avoidance Without Distance Information

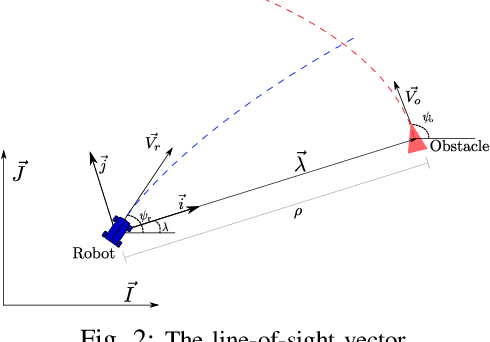
Biological evidence shows that animals are capable of evading eminent collision without using depth information, relying solely on looming stimuli. In robotics, collision avoidance among uncooperative vehicles requires measurement of relative distance to the obstacle. Small, low-cost mobile robots and UAVs might be unable to carry distance measuring sensors, like LIDARS and depth cameras. We propose a control framework suitable for a unicycle-like vehicle moving in a 2D plane that achieves collision avoidance. The control strategy is inspired by the reaction of invertebrates to approaching obstacles, relying exclusively on line-of-sight (LOS) angle, LOS angle rate, and time-to-collision as feedback. Those quantities can readily be estimated from a monocular camera vision system onboard a mobile robot. The proposed avoidance law commands the heading angle to circumvent a moving obstacle with unknown position, while the velocity controller is left as a degree of freedom to accomplish other mission objectives. Theoretical guarantees are provided to show that minimum separation between the vehicle and the obstacle is attained regardless of the exogenous tracking controller.

A Path Planning Framework for a Flying Robot in Close Proximity of Humans

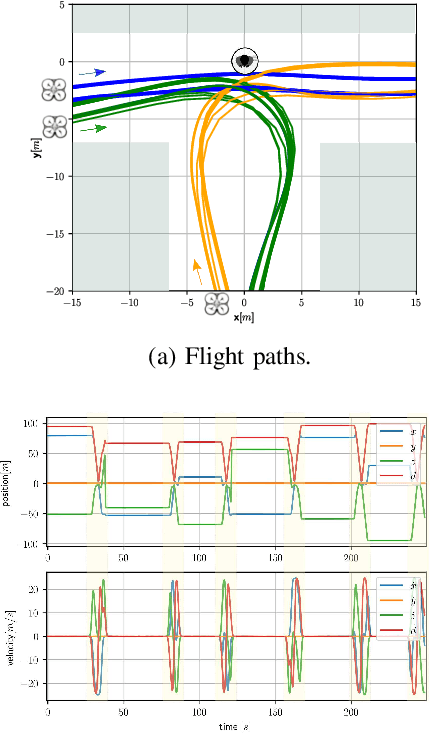
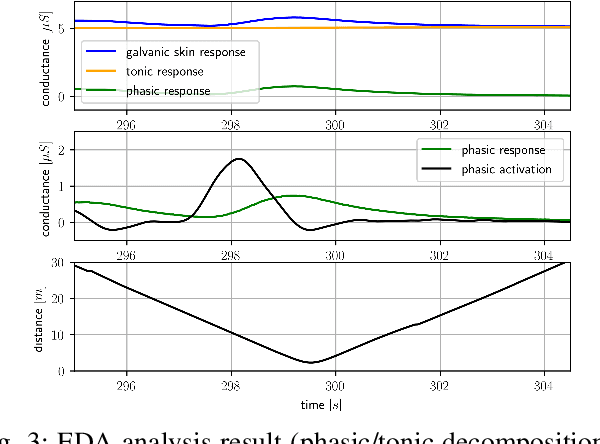
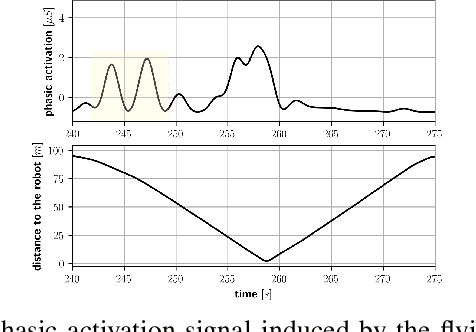
We present a path planning framework that takes into account the human's safety perception in the presence of a flying robot. The framework addresses two objectives: (i) estimation of the uncertain parameters of the proposed safety perception model based on test data collected using Virtual Reality (VR) testbed, and (ii) offline optimal control computation using the estimated safety perception model. Due to the unknown factors in the human tests data, it is not suitable to use standard regression techniques that minimize the mean squared error (MSE). We propose to use a Hidden Markov model (HMM) approach where human's attention is considered as a hidden state to infer whether the data samples are relevant to learn the safety perception model. The HMM approach improved log-likelihood over the standard least squares solution. For path planning, we use Bernstein polynomials for discretization, as the resulting path remains within the convex hull of the control points, providing guarantees for deconfliction with obstacles at low computational cost. An example of optimal trajectory generation using the learned human model is presented. The optimal trajectory generated using the proposed model results in reasonable safety distance from the human. In contrast, the paths generated using the standard regression model have undesirable shapes due to overfitting. The example demonstrates that the HMM approach has robustness to the unknown factors compared to the standard MSE model.