Safety-critical Control Under Partial Observability: Reach-Avoid POMDP meets Belief Space Control

Partially Observable Markov Decision Processes (POMDPs) provide a principled framework for robot decision-making under uncertainty. Solving reach-avoid POMDPs, however, requires coordinating three distinct behaviors: goal reaching, safety, and active information gathering to reduce uncertainty. Existing online POMDP solvers attempt to address all three within a single belief tree search, but this unified approach struggles with the conflicting time scales inherent to these objectives. We propose a layered, certificate-based control architecture that operates directly in belief space, decoupling goal reaching, information gathering, and safety into modular components. We introduce Belief Control Lyapunov Functions (BCLFs) that formalize information gathering as a Lyapunov convergence problem in belief space, and show how they can be learned via reinforcement learning. For safety, we develop Belief Control Barrier Functions (BCBFs) that leverage conformal prediction to provide probabilistic safety guarantees over finite horizons. The resulting control synthesis reduces to lightweight quadratic programs solvable in real time, even for non-Gaussian belief representations with dimension $>10^4$. Experiments in simulation and on a space-robotics platform demonstrate real-time performance and improved safety and task success compared to state-of-the-art constrained POMDP solvers.

Validation of Space Robotics in Underwater Environments via Disturbance Robustness Equivalency

We present an experimental validation framework for space robotics that leverages underwater environments to approximate microgravity dynamics. While neutral buoyancy conditions make underwater robotics an excellent platform for space robotics validation, there are still dynamical and environmental differences that need to be overcome. Given a high-level space mission specification, expressed in terms of a Signal Temporal Logic specification, we overcome these differences via the notion of maximal disturbance robustness of the mission. We formulate the motion planning problem such that the original space mission and the validation mission achieve the same disturbance robustness degree. The validation platform then executes its mission plan using a near-identical control strategy to the space mission where the closed-loop controller considers the spacecraft dynamics. Evaluating our validation framework relies on estimating disturbances during execution and comparing them to the disturbance robustness degree, providing practical evidence of operation in the space environment. Our evaluation features a dual-experiment setup: an underwater robot operating under near-neutral buoyancy conditions to validate the planning and control strategy of either an experimental planar spacecraft platform or a CubeSat in a high-fidelity space dynamics simulator.

Marinarium: a New Arena to Bring Maritime Robotics Closer to Shore

This paper presents the Marinarium, a modular and stand-alone underwater research facility designed to provide a realistic testbed for maritime and space-analog robotic experimentation in a resource-efficient manner. The Marinarium combines a fully instrumented underwater and aerial operational volume, extendable via a retractable roof for real-weather conditions, a digital twin in the SMaRCSim simulator and tight integration with a space robotics laboratory. All of these result from design choices aimed at bridging simulation, laboratory validation, and field conditions. We compare the Marinarium to similar existing infrastructures and illustrate how its design enables a set of experiments in four open research areas within field robotics. First, we exploit high-fidelity dynamics data from the tank to demonstrate the potential of learning-based system identification approaches applied to underwater vehicles. We further highlight the versatility of the multi-domain operating volume via a rendezvous mission with a heterogeneous fleet of robots across underwater, surface, and air. We then illustrate how the presented digital twin can be utilized to reduce the reality gap in underwater simulation. Finally, we demonstrate the potential of underwater surrogates for spacecraft navigation validation by executing spatiotemporally identical inspection tasks on a planar space-robot emulator and a neutrally buoyant \gls{rov}. In this work, by sharing the insights obtained and rationale behind the design and construction of the Marinarium, we hope to provide the field robotics research community with a blueprint for bridging the gap between controlled and real offshore and space robotics experimentation.

Exact Smooth Reformulations for Trajectory Optimization Under Signal Temporal Logic Specifications

We study motion planning under Signal Temporal Logic (STL), a useful formalism for specifying spatial-temporal requirements. We pose STL synthesis as a trajectory optimization problem leveraging the STL robustness semantics. To obtain a differentiable problem without approximation error, we introduce an exact reformulation of the max and min operators. The resulting method is exact, smooth, and sound. We validate it in numerical simulations, demonstrating its practical performance.

Collaborative Object Transportation in Space via Impact Interactions

We present a planning and control approach for collaborative transportation of objects in space by a team of robots. Object and robots in microgravity environments are not subject to friction but are instead free floating. This property is key to how we approach the transportation problem: the passive objects are controlled by impact interactions with the controlled robots. In particular, given a high-level Signal Temporal Logic (STL) specification of the transportation task, we synthesize motion plans for the robots to maximize the specification satisfaction in terms of spatial STL robustness. Given that the physical impact interactions are complex and hard to model precisely, we also present an alternative formulation maximizing the permissible uncertainty in a simplified kinematic impact model. We define the full planning and control stack required to solve the object transportation problem; an offline planner, an online replanner, and a low-level model-predictive control scheme for each of the robots. We show the method in a high-fidelity simulator for a variety of scenarios and present experimental validation of 2-robot, 1-object scenarios on a freeflyer platform.

Towards Open-Source and Modular Space Systems with ATMOS

In the near future, autonomous space systems will compose a large number of the spacecraft being deployed. Their tasks will involve autonomous rendezvous and proximity operations with large structures, such as inspections or assembly of orbiting space stations and maintenance and human-assistance tasks over shared workspaces. To promote replicable and reliable scientific results for autonomous control of spacecraft, we present the design of a space systems laboratory based on open-source and modular software and hardware. The simulation software provides a software-in-the-loop (SITL) architecture that seamlessly transfers simulated results to the ATMOS platforms, developed for testing of multi-agent autonomy schemes for microgravity. The manuscript presents the KTH space systems laboratory facilities and the ATMOS platform as open-source hardware and software contributions. Preliminary results showcase SITL and real testing.

Robust STL Control Synthesis under Maximal Disturbance Sets

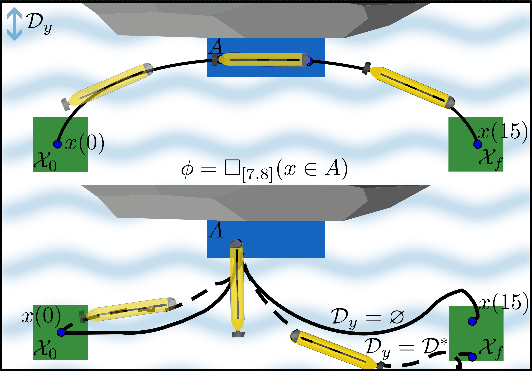
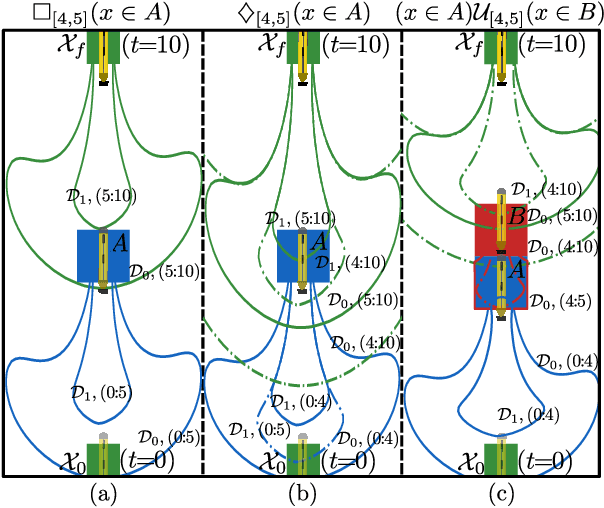
This work addresses maximally robust control synthesis under unknown disturbances. We consider a general nonlinear system, subject to a Signal Temporal Logic (STL) specification, and wish to jointly synthesize the maximal possible disturbance bounds and the corresponding controllers that ensure the STL specification is satisfied under these bounds. Many works have considered STL satisfaction under given bounded disturbances. Yet, to the authors' best knowledge, this is the first work that aims to maximize the permissible disturbance set and find the corresponding controllers that ensure satisfying the STL specification with maximum disturbance robustness. We extend the notion of disturbance-robust semantics for STL, which is a property of a specification, dynamical system, and controller, and provide an algorithm to get the maximal disturbance robust controllers satisfying an STL specification using Hamilton-Jacobi reachability. We show its soundness and provide a simulation example with an Autonomous Underwater Vehicle (AUV).

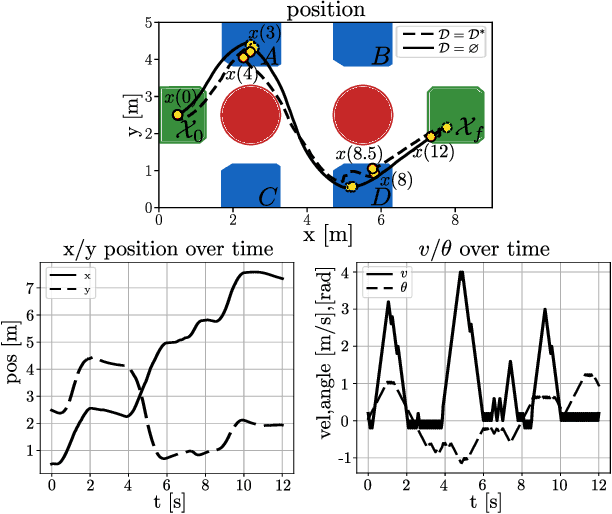
Temporally Robust Multi-Agent STL Motion Planning in Continuous Time

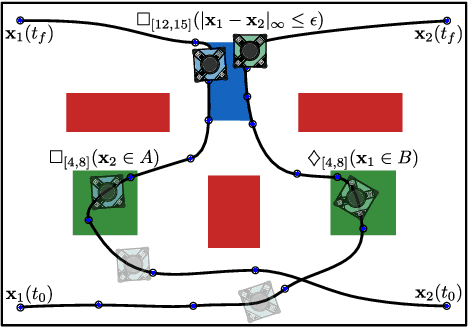
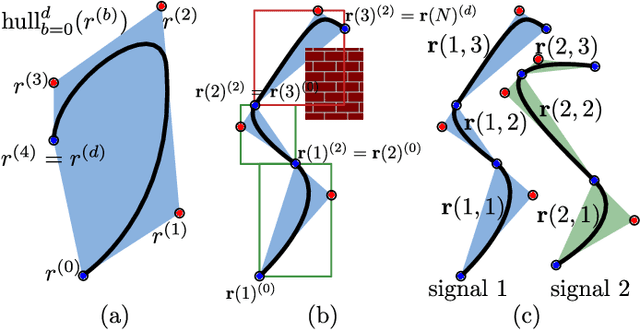
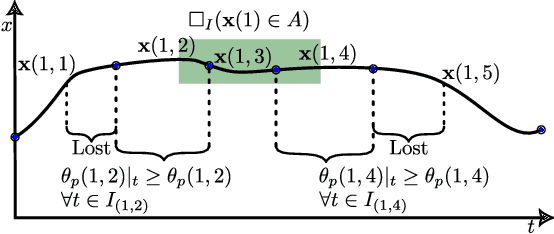
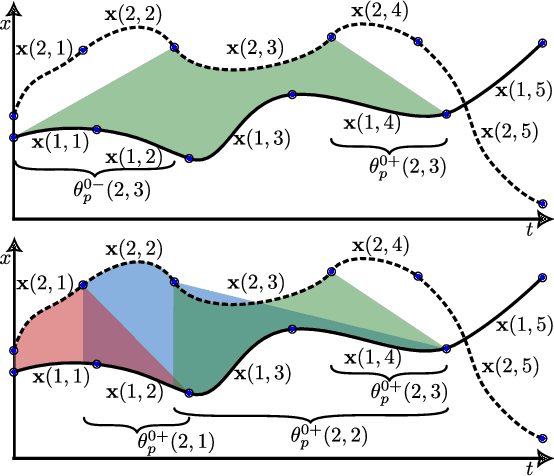
Signal Temporal Logic (STL) is a formal language over continuous-time signals (such as trajectories of a multi-agent system) that allows for the specification of complex spatial and temporal system requirements (such as staying sufficiently close to each other within certain time intervals). To promote robustness in multi-agent motion planning with such complex requirements, we consider motion planning with the goal of maximizing the temporal robustness of their joint STL specification, i.e. maximizing the permissible time shifts of each agent's trajectory while still satisfying the STL specification. Previous methods presented temporally robust motion planning and control in a discrete-time Mixed Integer Linear Programming (MILP) optimization scheme. In contrast, we parameterize the trajectory by continuous B\'ezier curves, where the curvature and the time-traversal of the trajectory are parameterized individually. We show an algorithm generating continuous-time temporally robust trajectories and prove soundness of our approach. Moreover, we empirically show that our parametrization realizes this with a considerable speed-up compared to state-of-the-art methods based on constant interval time discretization.

From Human Walking to Bipedal Robot Locomotion: Reflex Inspired Compensation on Planned and Unplanned Downsteps

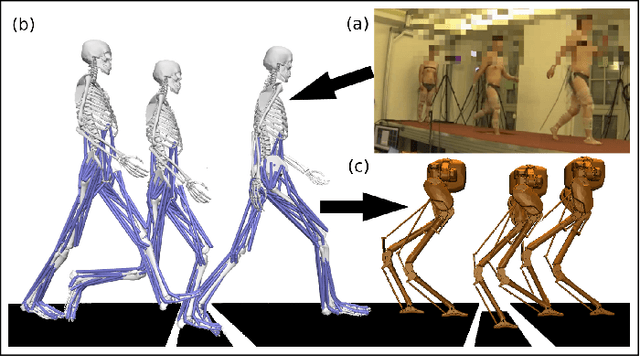
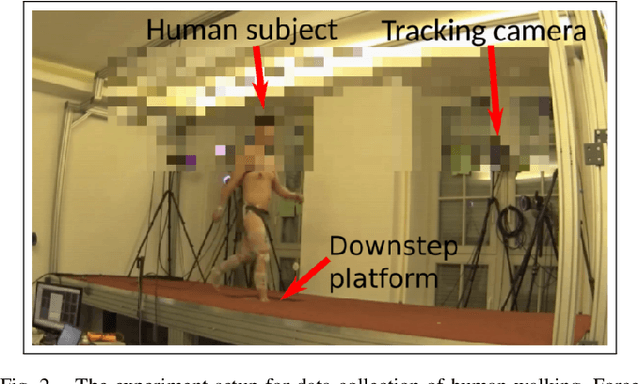
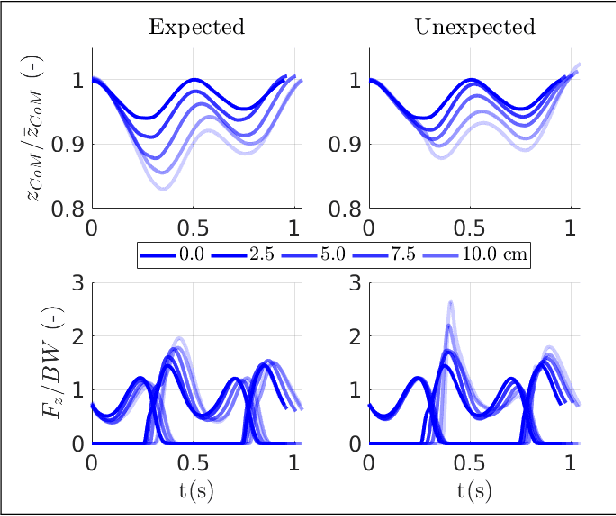
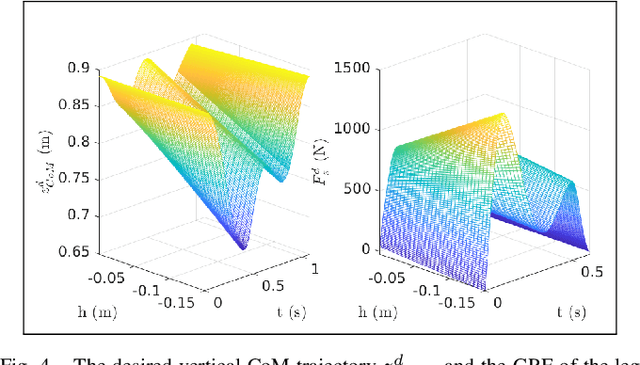
Humans are able to negotiate downstep behaviors -- both planned and unplanned -- with remarkable agility and ease. The goal of this paper is to systematically study the translation of this human behavior to bipedal walking robots, even if the morphology is inherently different. Concretely, we begin with human data wherein planned and unplanned downsteps are taken. We analyze this data from the perspective of reduced-order modeling of the human, encoding the center of mass (CoM) kinematics and contact forces, which allows for the translation of these behaviors into the corresponding reduced-order model of a bipedal robot. We embed the resulting behaviors into the full-order dynamics of a bipedal robot via nonlinear optimization-based controllers. The end result is the demonstration of planned and unplanned downsteps in simulation on an underactuated walking robot.