Safe Online Dynamics Learning with Initially Unknown Models and Infeasible Safety Certificates

Safety-critical control tasks with high levels of uncertainty are becoming increasingly common. Typically, techniques that guarantee safety during learning and control utilize constraint-based safety certificates, which can be leveraged to compute safe control inputs. However, excessive model uncertainty can render robust safety certification methods or infeasible, meaning no control input satisfies the constraints imposed by the safety certificate. This paper considers a learning-based setting with a robust safety certificate based on a control barrier function (CBF) second-order cone program. If the control barrier function certificate is feasible, our approach leverages it to guarantee safety. Otherwise, our method explores the system dynamics to collect data and recover the feasibility of the control barrier function constraint. To this end, we employ a method inspired by well-established tools from Bayesian optimization. We show that if the sampling frequency is high enough, we recover the feasibility of the robust CBF certificate, guaranteeing safety. Our approach requires no prior model and corresponds, to the best of our knowledge, to the first algorithm that guarantees safety in settings with occasionally infeasible safety certificates without requiring a backup non-learning-based controller.

Verifiably Safe Reinforcement Learning with Probabilistic Guarantees via Temporal Logic

Reinforcement Learning (RL) can solve complex tasks but does not intrinsically provide any guarantees on system behavior. For real-world systems that fulfill safety-critical tasks, such guarantees on safety specifications are necessary. To bridge this gap, we propose a verifiably safe RL procedure with probabilistic guarantees. First, our approach probabilistically verifies a candidate controller with respect to a temporal logic specification, while randomizing the controller's inputs within a bounded set. Then, we use RL to improve the performance of this probabilistically verified, i.e. safe, controller and explore in the same bounded set around the controller's input as was randomized over in the verification step. Finally, we calculate probabilistic safety guarantees with respect to temporal logic specifications for the learned agent. Our approach is efficient for continuous action and state spaces and separates safety verification and performance improvement into two independent steps. We evaluate our approach on a safe evasion task where a robot has to evade a dynamic obstacle in a specific manner while trying to reach a goal. The results show that our verifiably safe RL approach leads to efficient learning and performance improvements while maintaining safety specifications.

Robust Locomotion on Legged Robots through Planning on Motion Primitive Graphs

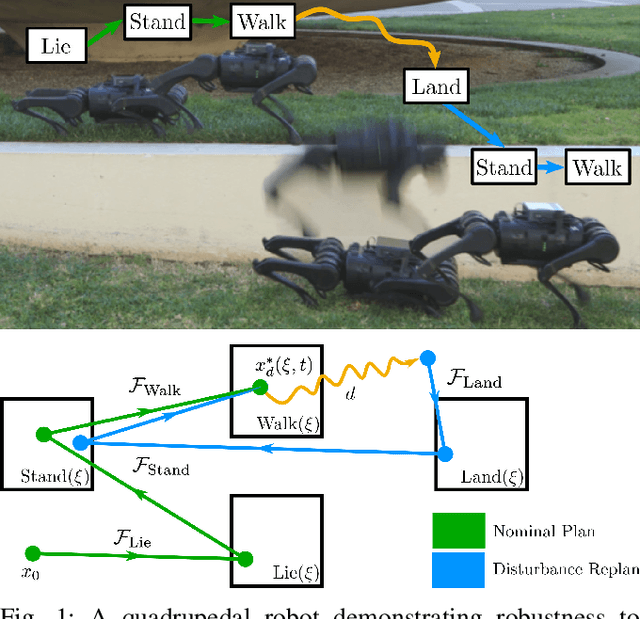
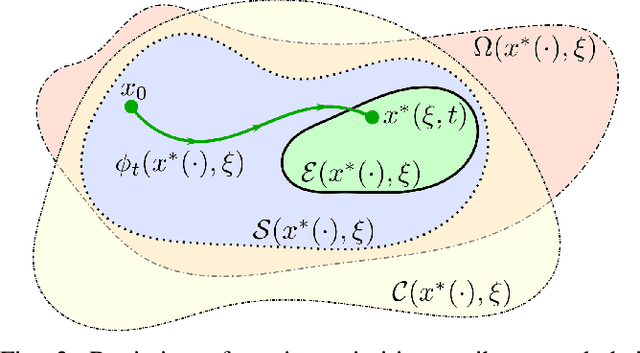
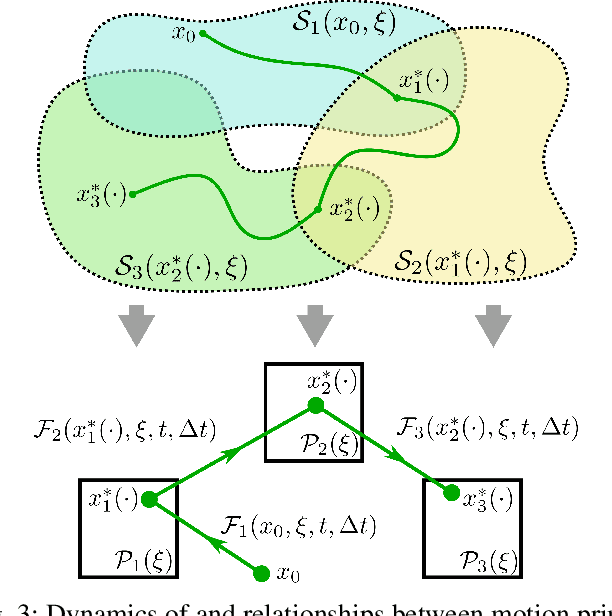
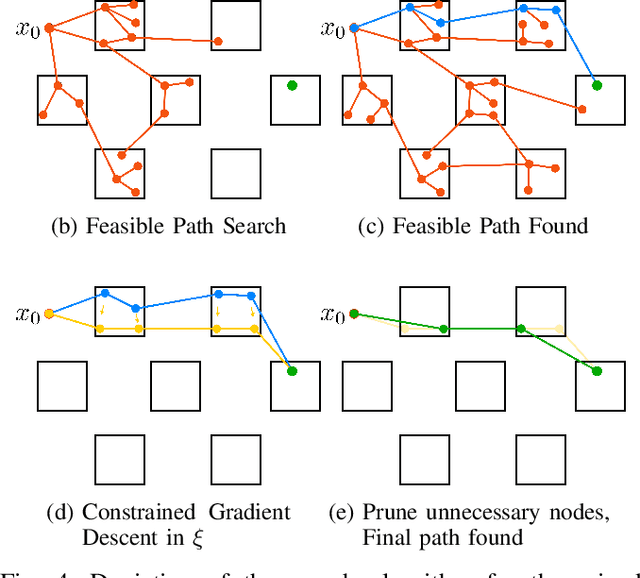
The functional demands of robotic systems often require completing various tasks or behaviors under the effect of disturbances or uncertain environments. Of increasing interest is the autonomy for dynamic robots, such as multirotors, motor vehicles, and legged platforms. Here, disturbances and environmental conditions can have significant impact on the successful performance of the individual dynamic behaviors, referred to as "motion primitives". Despite this, robustness can be achieved by switching to and transitioning through suitable motion primitives. This paper contributes such a method by presenting an abstraction of the motion primitive dynamics and a corresponding "motion primitive transfer function". From this, a mixed discrete and continuous "motion primitive graph" is constructed, and an algorithm capable of online search of this graph is detailed. The result is a framework capable of realizing holistic robustness on dynamic systems. This is experimentally demonstrated for a set of motion primitives on a quadrupedal robot, subject to various environmental and intentional disturbances.

From Human Walking to Bipedal Robot Locomotion: Reflex Inspired Compensation on Planned and Unplanned Downsteps

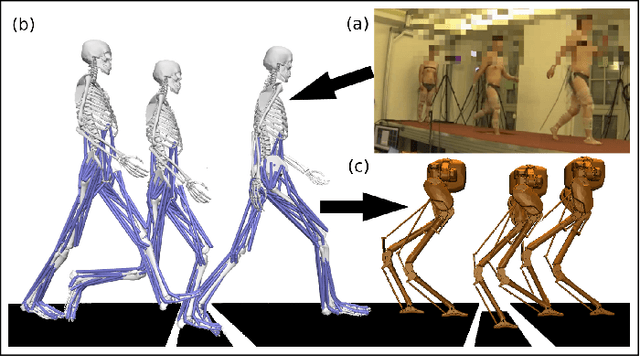
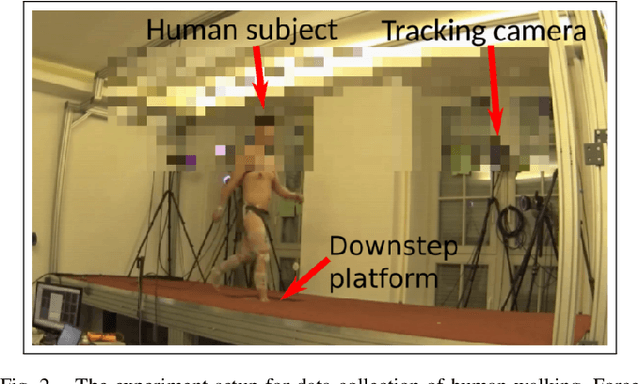
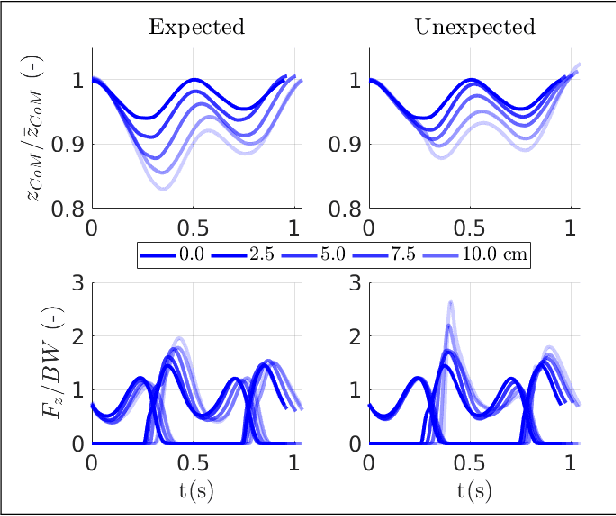
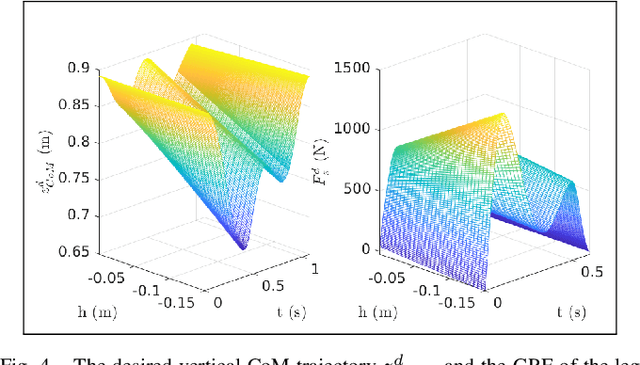
Humans are able to negotiate downstep behaviors -- both planned and unplanned -- with remarkable agility and ease. The goal of this paper is to systematically study the translation of this human behavior to bipedal walking robots, even if the morphology is inherently different. Concretely, we begin with human data wherein planned and unplanned downsteps are taken. We analyze this data from the perspective of reduced-order modeling of the human, encoding the center of mass (CoM) kinematics and contact forces, which allows for the translation of these behaviors into the corresponding reduced-order model of a bipedal robot. We embed the resulting behaviors into the full-order dynamics of a bipedal robot via nonlinear optimization-based controllers. The end result is the demonstration of planned and unplanned downsteps in simulation on an underactuated walking robot.

Robust Disturbance Rejection for Robotic Bipedal Walking: System-Level-Synthesis with Step-to-step Dynamics Approximation

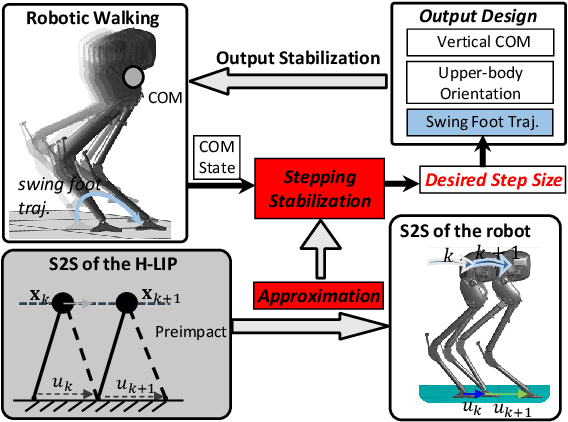
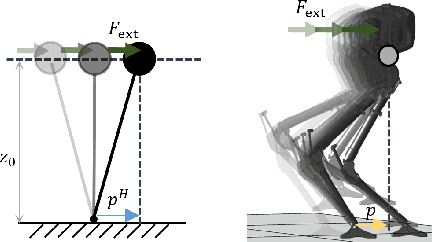
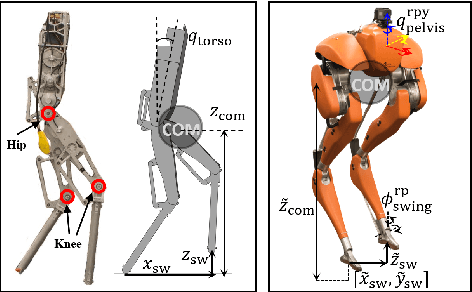
We present a stepping stabilization control that addresses external push disturbances on bipedal walking robots. The stepping control is synthesized based on the step-to-step (S2S) dynamics of the robot that is controlled to have an approximately constant center of mass (COM) height. We first learn a linear S2S dynamics with bounded model discrepancy from the undisturbed walking behaviors of the robot, where the walking step size is taken as the control input to the S2S dynamics. External pushes are then considered as disturbances to the learned S2S (L-S2S) dynamics. We then apply the system-level-synthesis (SLS) approach on the disturbed L-S2S dynamics to robustly stabilize the robot to the desired walking while satisfying the kinematic constraints of the robot. We successfully realize the proposed approach on the walking of the bipedal robot AMBER and Cassie subject to push disturbances, showing that the approach is general, effective, and computationally-efficient for robust disturbance rejection.

Bipedal Walking on Constrained Footholds: Momentum Regulation via Vertical COM Control

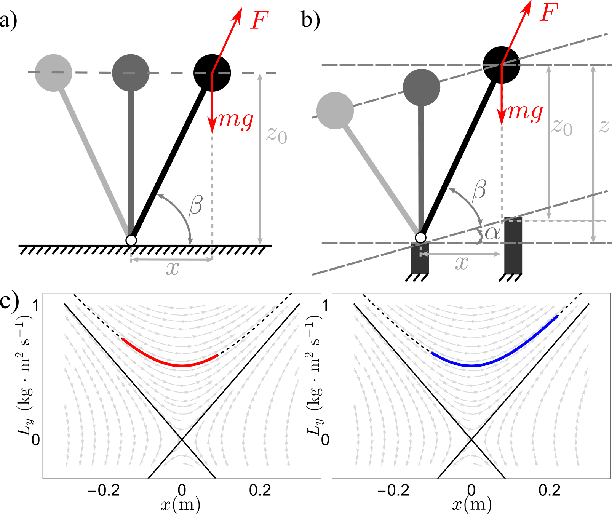
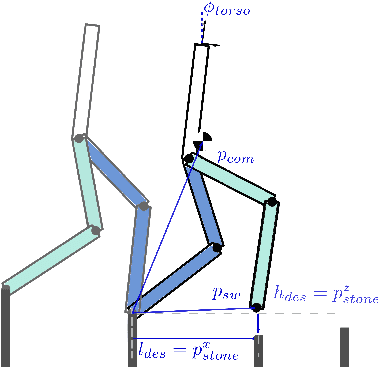
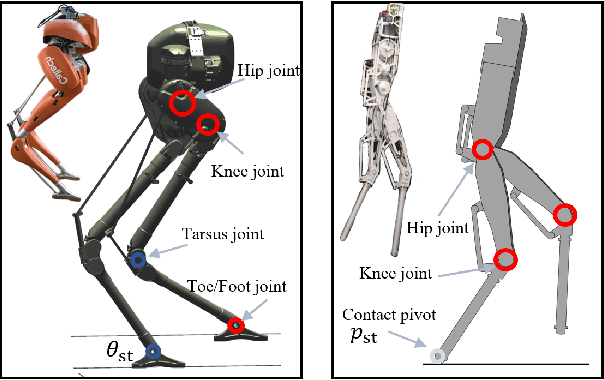
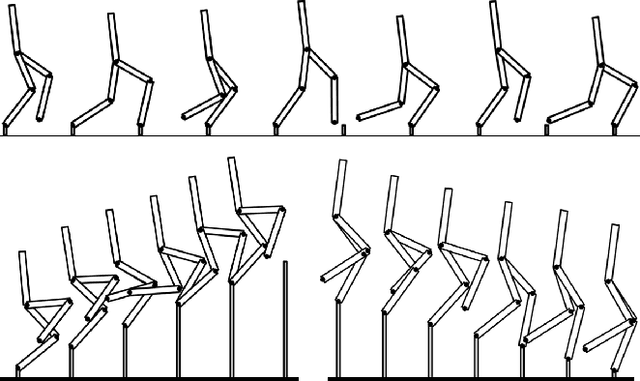
This paper presents an online walking gait synthesis and a feedback control methodology to enable stable walking on constrained footholds for bipedal robots. For this challenging task, the foot placement and center of pressure cannot be changed, which hinders the application of state-of-art stepping controllers or zero-moment-point (ZMP) based approaches for walking generation. As a result, this paper takes a different approach to modulate the change of the angular momentum about the foot-ground contact pivot at the discrete impact with vertical center of mass (COM) velocity. We utilize the underactuated Linear Inverted Pendulum (LIP) model for approximating the underactuated walking dynamics to provide the desired post-impact angular momentum for each step. Outputs are constructed via online optimization combined with closed-form polynomials and then tracked via a quadratic program based controller. This method is implemented online on two robot models, AMBER and Cassie, for which stable walking behaviors with constrained footholds are realized on flat ground, stairs, and randomly located stepping stones.

SLIP Walking over Rough Terrain via H-LIP Stepping and Backstepping-Barrier Function Inspired Quadratic Program

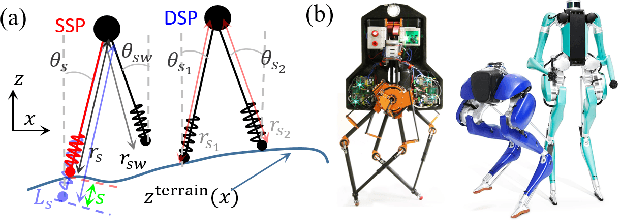
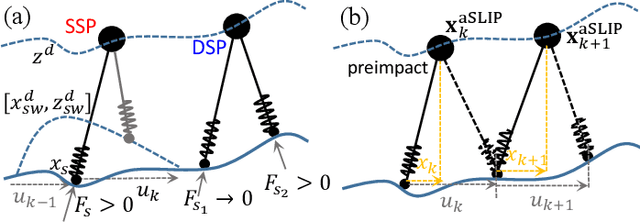
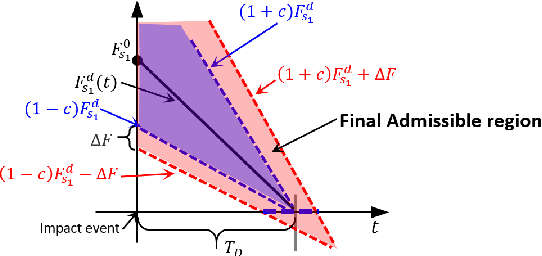
We present an advanced and novel control method to enable actuated Spring Loaded Inverted Pendulum model to walk over rough and challenging terrains. The high-level philosophy is the decoupling of the controls of the vertical and horizontal states. The vertical state is controlled via Backstepping-Barrier Function (BBF) based quadratic programs: a combination of control Lyapunov backstepping and control barrier function, both of which provide inequality constraints on the inputs. The horizontal state is stabilized via Hybrid-Linear Inverted Pendulum (H-LIP) based stepping, which has a closed-form formulation. Therefore, the implementation is computationally-efficient. We evaluate our method in simulation, which demonstrates the aSLIP walking over various terrains, including slopes, stairs, and general rough terrains with uncertainties.

3D Underactuated Bipedal Walking via H-LIP based Gait Synthesis and Stepping Stabilization

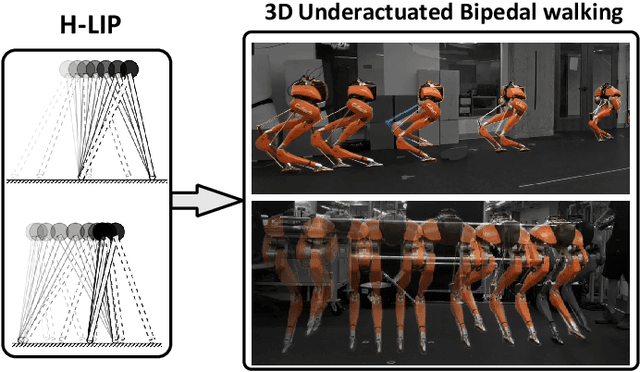
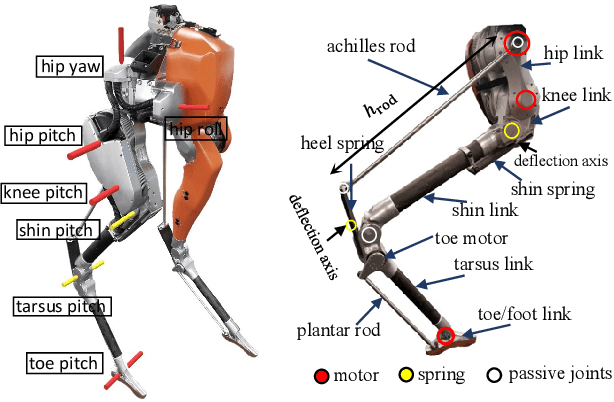
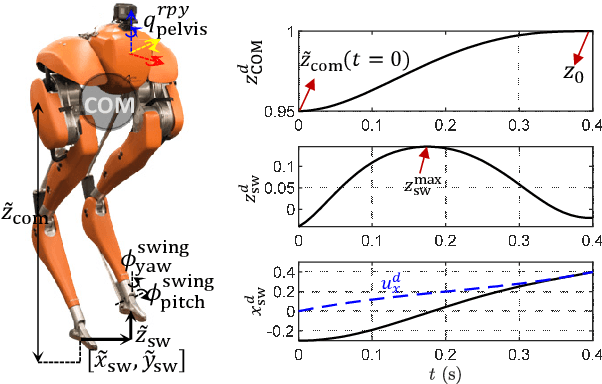
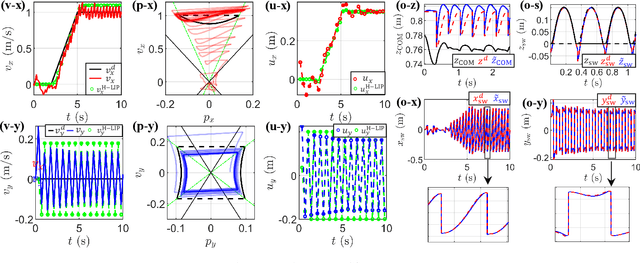
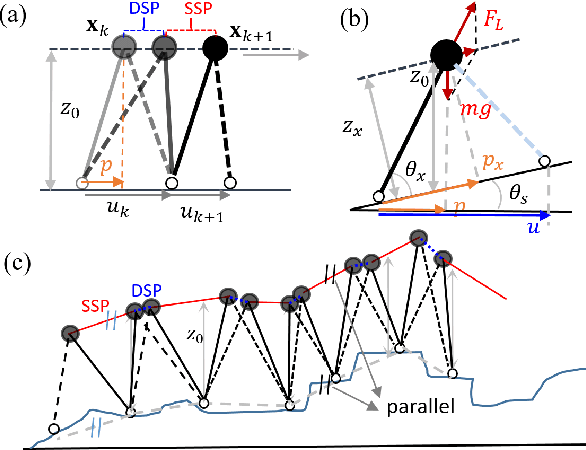
In this paper, we present a Hybrid-Linear Inverted Pendulum (H-LIP) based approach for synthesizing and stabilizing 3D underactuated bipedal walking. The H-LIP model is proposed to capture the essential components of the underactuated part and actuated part of the robotic walking. The walking gait of the robot is then synthesized based on the H-LIP. We comprehensively characterize the periodic orbits of the H-LIP and provably derive their stepping stabilization. The step-to-step (S2S) dynamics of the H-LIP is then utilized to approximate the S2S dynamics of the horizontal state of the center of mass (COM) of the robotic walking, which results in a H-LIP based stepping controller to provide desired step sizes to stabilize the robotic walking. By realizing the desired step sizes, the robot achieves dynamic and stable walking. The approach is evaluated in both simulation and experiment on the 3D underactuated bipedal robot Cassie, which demonstrate dynamic walking behaviors with both versatility and robustness.

Global Position Control on Underactuated Bipedal Robots: Step-to-step Dynamics Approximation for Step Planning

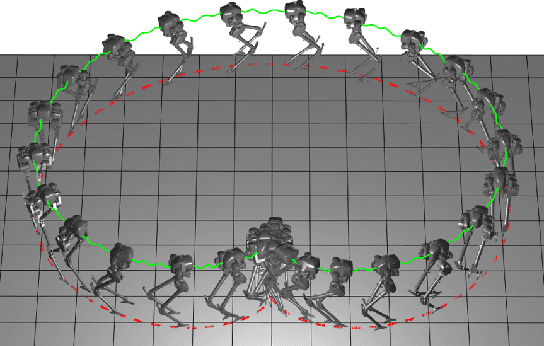
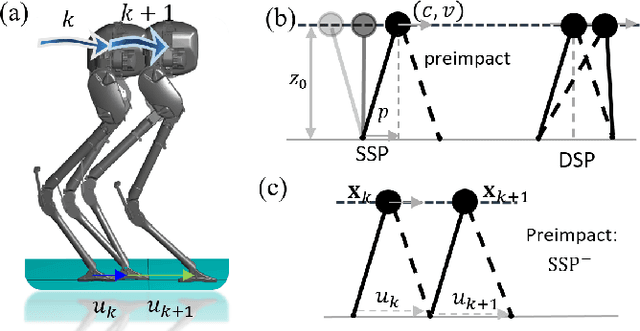
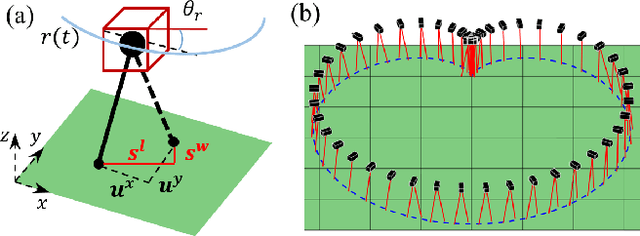
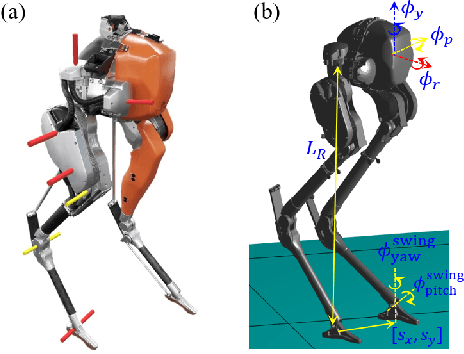
Global position control for underactuated bipedal walking is a challenging problem due to the lack of actuation on the feet of the robots. In this paper, we apply the Hybrid-Linear Inverted Pendulum (H-LIP) based stepping on 3D underactuated bipedal robots for global position control. The step-to-step (S2S) dynamics of the H-LIP walking approximates the actual S2S dynamics of the walking of the robot, where the step size is considered as the input. Thus the feedback controller based on the H-LIP approximately controls the robot to behave like the H-LIP, the differences between which stay in an error invariant set. Model Predictive Control (MPC) is applied to the H-LIP for global position control in 3D. The H-LIP stepping then generates desired step sizes for the robot to track. Moreover, turning behavior is integrated with the step planning. The proposed framework is verified on the 3D underactuated bipedal robot Cassie in simulation together with a proof-of-concept experiment.

Comparative Analysis of Control Barrier Functions and Artificial Potential Fields for Obstacle Avoidance

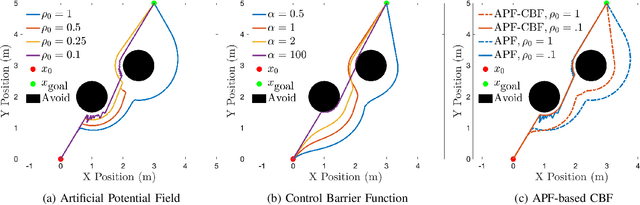
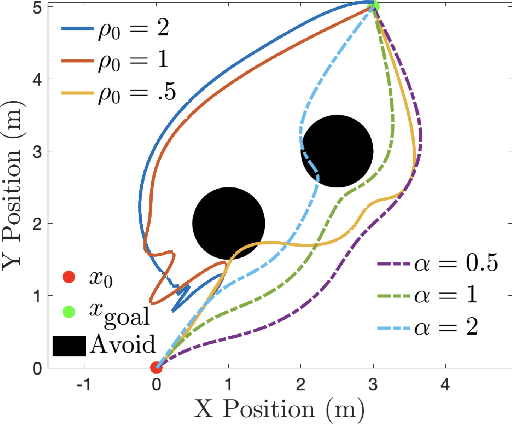
Artificial potential fields (APFs) and their variants have been a staple for collision avoidance of mobile robots and manipulators for almost 40 years. Its model-independent nature, ease of implementation, and real-time performance have played a large role in its continued success over the years. Control barrier functions (CBFs), on the other hand, are a more recent development, commonly used to guarantee safety for nonlinear systems in real-time in the form of a filter on a nominal controller. In this paper, we address the connections between APFs and CBFs. At a theoretic level, we prove that APFs are a special case of CBFs: given a APF one obtains a CBFs, while the converse is not true. Additionally, we prove that CBFs obtained from APFs have additional beneficial properties and can be applied to nonlinear systems. Practically, we compare the performance of APFs and CBFs in the context of obstacle avoidance on simple illustrative examples and for a quadrotor, both in simulation and on hardware using onboard sensing. These comparisons demonstrate that CBFs outperform APFs.