Multi-Timescale Dynamics Model Bayesian Optimization for Plasma Stabilization in Tokamaks

Machine learning algorithms often struggle to control complex real-world systems. In the case of nuclear fusion, these challenges are exacerbated, as the dynamics are notoriously complex, data is poor, hardware is subject to failures, and experiments often affect dynamics beyond the experiment's duration. Existing tools like reinforcement learning, supervised learning, and Bayesian optimization address some of these challenges but fail to provide a comprehensive solution. To overcome these limitations, we present a multi-scale Bayesian optimization approach that integrates a high-frequency data-driven dynamics model with a low-frequency Gaussian process. By updating the Gaussian process between experiments, the method rapidly adapts to new data, refining the predictions of the less reliable dynamical model. We validate our approach by controlling tearing instabilities in the DIII-D nuclear fusion plant. Offline testing on historical data shows that our method significantly outperforms several baselines. Results on live experiments on the DIII-D tokamak, conducted under high-performance plasma scenarios prone to instabilities, shows a 50% success rate, marking a 117% improvement over historical outcomes.

Learning Safe Control via On-the-Fly Bandit Exploration

Control tasks with safety requirements under high levels of model uncertainty are increasingly common. Machine learning techniques are frequently used to address such tasks, typically by leveraging model error bounds to specify robust constraint-based safety filters. However, if the learned model uncertainty is very high, the corresponding filters are potentially invalid, meaning no control input satisfies the constraints imposed by the safety filter. While most works address this issue by assuming some form of safe backup controller, ours tackles it by collecting additional data on the fly using a Gaussian process bandit-type algorithm. We combine a control barrier function with a learned model to specify a robust certificate that ensures safety if feasible. Whenever infeasibility occurs, we leverage the control barrier function to guide exploration, ensuring the collected data contributes toward the closed-loop system safety. By combining a safety filter with exploration in this manner, our method provably achieves safety in a setting that allows for a zero-mean prior dynamics model, without requiring a backup controller. To the best of our knowledge, it is the first safe learning-based control method that achieves this.

Koopman-Equivariant Gaussian Processes

Credible forecasting and representation learning of dynamical systems are of ever-increasing importance for reliable decision-making. To that end, we propose a family of Gaussian processes (GP) for dynamical systems with linear time-invariant responses, which are nonlinear only in initial conditions. This linearity allows us to tractably quantify forecasting and representational uncertainty, simultaneously alleviating the challenge of computing the distribution of trajectories from a GP-based dynamical system and enabling a new probabilistic treatment of learning Koopman operator representations. Using a trajectory-based equivariance -- which we refer to as \textit{Koopman equivariance} -- we obtain a GP model with enhanced generalization capabilities. To allow for large-scale regression, we equip our framework with variational inference based on suitable inducing points. Experiments demonstrate on-par and often better forecasting performance compared to kernel-based methods for learning dynamical systems.

Safe Online Dynamics Learning with Initially Unknown Models and Infeasible Safety Certificates

Safety-critical control tasks with high levels of uncertainty are becoming increasingly common. Typically, techniques that guarantee safety during learning and control utilize constraint-based safety certificates, which can be leveraged to compute safe control inputs. However, excessive model uncertainty can render robust safety certification methods or infeasible, meaning no control input satisfies the constraints imposed by the safety certificate. This paper considers a learning-based setting with a robust safety certificate based on a control barrier function (CBF) second-order cone program. If the control barrier function certificate is feasible, our approach leverages it to guarantee safety. Otherwise, our method explores the system dynamics to collect data and recover the feasibility of the control barrier function constraint. To this end, we employ a method inspired by well-established tools from Bayesian optimization. We show that if the sampling frequency is high enough, we recover the feasibility of the robust CBF certificate, guaranteeing safety. Our approach requires no prior model and corresponds, to the best of our knowledge, to the first algorithm that guarantees safety in settings with occasionally infeasible safety certificates without requiring a backup non-learning-based controller.

Online Constraint Tightening in Stochastic Model Predictive Control: A Regression Approach

Solving chance-constrained stochastic optimal control problems is a significant challenge in control. This is because no analytical solutions exist for up to a handful of special cases. A common and computationally efficient approach for tackling chance-constrained stochastic optimal control problems consists of reformulating the chance constraints as hard constraints with a constraint-tightening parameter. However, in such approaches, the choice of constraint-tightening parameter remains challenging, and guarantees can mostly be obtained assuming that the process noise distribution is known a priori. Moreover, the chance constraints are often not tightly satisfied, leading to unnecessarily high costs. This work proposes a data-driven approach for learning the constraint-tightening parameters online during control. To this end, we reformulate the choice of constraint-tightening parameter for the closed-loop as a binary regression problem. We then leverage a highly expressive \gls{gp} model for binary regression to approximate the smallest constraint-tightening parameters that satisfy the chance constraints. By tuning the algorithm parameters appropriately, we show that the resulting constraint-tightening parameters satisfy the chance constraints up to an arbitrarily small margin with high probability. Our approach yields constraint-tightening parameters that tightly satisfy the chance constraints in numerical experiments, resulting in a lower average cost than three other state-of-the-art approaches.

Sharp Calibrated Gaussian Processes

While Gaussian processes are a mainstay for various engineering and scientific applications, the uncertainty estimates don't satisfy frequentist guarantees, and can be miscalibrated in practice. State-of-the-art approaches for designing calibrated models rely on inflating the Gaussian process posterior variance, which yields confidence intervals that are potentially too coarse. To remedy this, we present a calibration approach that generates predictive quantiles using a computation inspired by the vanilla Gaussian process posterior variance, but using a different set of hyperparameters, chosen to satisfy an empirical calibration constraint. This results in a calibration approach that is considerably more flexible than existing approaches. Our approach is shown to yield a calibrated model under reasonable assumptions. Furthermore, it outperforms existing approaches not only when employed for calibrated regression, but also to inform the design of Bayesian optimization algorithms.

Dext-Gen: Dexterous Grasping in Sparse Reward Environments with Full Orientation Control

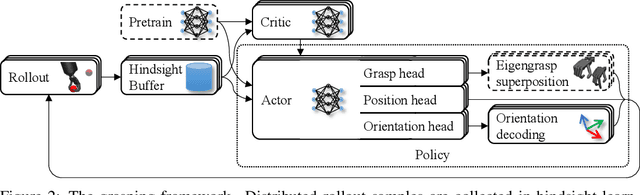
Reinforcement learning is a promising method for robotic grasping as it can learn effective reaching and grasping policies in difficult scenarios. However, achieving human-like manipulation capabilities with sophisticated robotic hands is challenging because of the problem's high dimensionality. Although remedies such as reward shaping or expert demonstrations can be employed to overcome this issue, they often lead to oversimplified and biased policies. We present Dext-Gen, a reinforcement learning framework for Dexterous Grasping in sparse reward ENvironments that is applicable to a variety of grippers and learns unbiased and intricate policies. Full orientation control of the gripper and object is achieved through smooth orientation representation. Our approach has reasonable training durations and provides the option to include desired prior knowledge. The effectiveness and adaptability of the framework to different scenarios is demonstrated in simulated experiments.

Structure-Preserving Learning Using Gaussian Processes and Variational Integrators

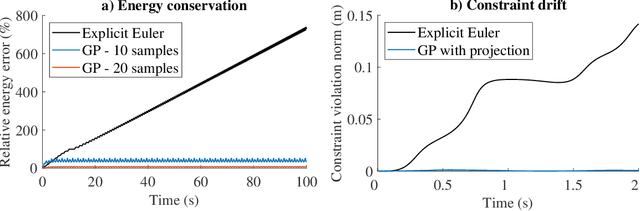
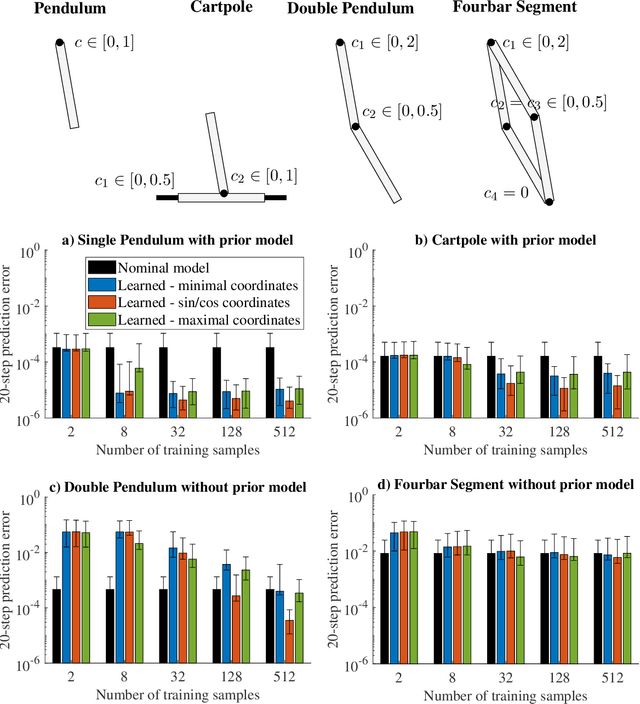
Gaussian process regression is often applied for learning unknown systems and specifying the uncertainty of the learned model. When using Gaussian process regression to learn unknown systems, a commonly considered approach consists of learning the residual dynamics after applying some standard discretization, which might however not be appropriate for the system at hand. Variational integrators are a less common yet promising approach to discretization, as they retain physical properties of the underlying system, such as energy conservation or satisfaction of explicit constraints. In this work, we propose the combination of a variational integrator for the nominal dynamics of a mechanical system and learning residual dynamics with Gaussian process regression. We extend our approach to systems with known kinematic constraints and provide formal bounds on the prediction uncertainty. The simulative evaluation of the proposed method shows desirable energy conservation properties in accordance with the theoretical results and demonstrates the capability of treating constrained dynamical systems.

Gaussian Process Uniform Error Bounds with Unknown Hyperparameters for Safety-Critical Applications

Gaussian processes have become a promising tool for various safety-critical settings, since the posterior variance can be used to directly estimate the model error and quantify risk. However, state-of-the-art techniques for safety-critical settings hinge on the assumption that the kernel hyperparameters are known, which does not apply in general. To mitigate this, we introduce robust Gaussian process uniform error bounds in settings with unknown hyperparameters. Our approach computes a confidence region in the space of hyperparameters, which enables us to obtain a probabilistic upper bound for the model error of a Gaussian process with arbitrary hyperparameters. We do not require to know any bounds for the hyperparameters a priori, which is an assumption commonly found in related work. Instead, we are able to derive bounds from data in an intuitive fashion. We additionally employ the proposed technique to derive performance guarantees for a class of learning-based control problems. Experiments show that the bound performs significantly better than vanilla and fully Bayesian Gaussian processes.

Gaussian Process-based Stochastic Model Predictive Control for Overtaking in Autonomous Racing

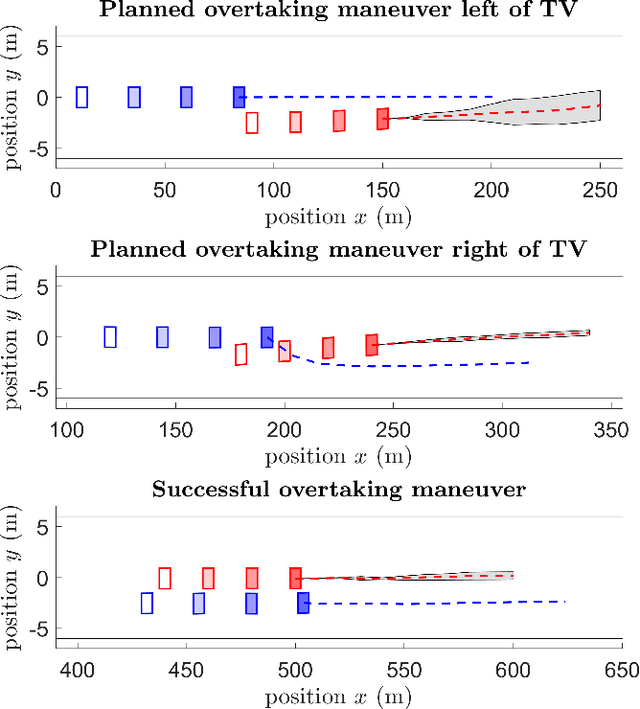
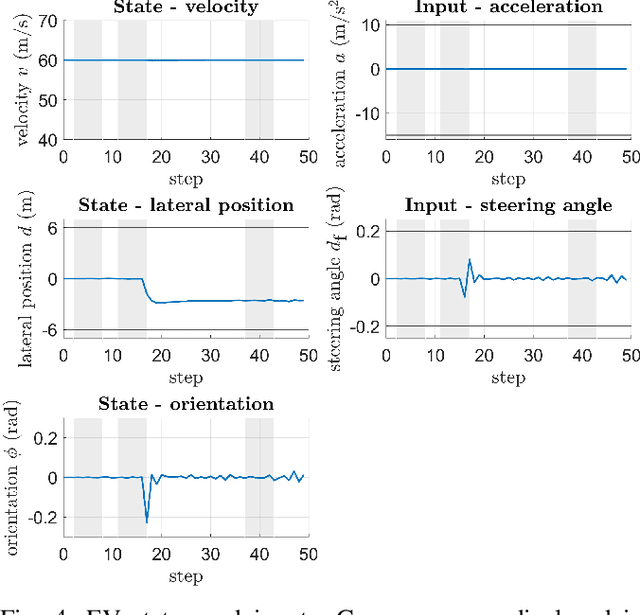
A fundamental aspect of racing is overtaking other race cars. Whereas previous research on autonomous racing has majorly focused on lap-time optimization, here, we propose a method to plan overtaking maneuvers in autonomous racing. A Gaussian process is used to learn the behavior of the leading vehicle. Based on the outputs of the Gaussian process, a stochastic Model Predictive Control algorithm plans optimistic trajectories, such that the controlled autonomous race car is able to overtake the leading vehicle. The proposed method is tested in a simple simulation scenario.