SwarmGPT-Primitive: A Language-Driven Choreographer for Drone Swarms Using Safe Motion Primitive Composition

Catalyzed by advancements in hardware and software, drone performances are increasingly making their mark in the entertainment industry. However, designing smooth and safe choreographies for drone swarms is complex and often requires expert domain knowledge. In this work, we introduce SwarmGPT-Primitive, a language-based choreographer that integrates the reasoning capabilities of large language models (LLMs) with safe motion planning to facilitate deployable drone swarm choreographies. The LLM composes choreographies for a given piece of music by utilizing a library of motion primitives; the language-based choreographer is augmented with an optimization-based safety filter, which certifies the choreography for real-world deployment by making minimal adjustments when feasibility and safety constraints are violated. The overall SwarmGPT-Primitive framework decouples choreographic design from safe motion planning, which allows non-expert users to re-prompt and refine compositions without concerns about compliance with constraints such as avoiding collisions or downwash effects or satisfying actuation limits. We demonstrate our approach through simulations and experiments with swarms of up to 20 drones performing choreographies designed based on various songs, highlighting the system's ability to generate effective and synchronized drone choreographies for real-world deployment.

Reinforcement Learning with Lie Group Orientations for Robotics

Handling orientations of robots and objects is a crucial aspect of many applications. Yet, ever so often, there is a lack of mathematical correctness when dealing with orientations, especially in learning pipelines involving, for example, artificial neural networks. In this paper, we investigate reinforcement learning with orientations and propose a simple modification of the network's input and output that adheres to the Lie group structure of orientations. As a result, we obtain an easy and efficient implementation that is directly usable with existing learning libraries and achieves significantly better performance than other common orientation representations. We briefly introduce Lie theory specifically for orientations in robotics to motivate and outline our approach. Subsequently, a thorough empirical evaluation of different combinations of orientation representations for states and actions demonstrates the superior performance of our proposed approach in different scenarios, including: direct orientation control, end effector orientation control, and pick-and-place tasks.

Dext-Gen: Dexterous Grasping in Sparse Reward Environments with Full Orientation Control

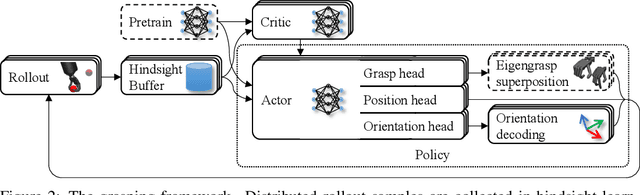
Reinforcement learning is a promising method for robotic grasping as it can learn effective reaching and grasping policies in difficult scenarios. However, achieving human-like manipulation capabilities with sophisticated robotic hands is challenging because of the problem's high dimensionality. Although remedies such as reward shaping or expert demonstrations can be employed to overcome this issue, they often lead to oversimplified and biased policies. We present Dext-Gen, a reinforcement learning framework for Dexterous Grasping in sparse reward ENvironments that is applicable to a variety of grippers and learns unbiased and intricate policies. Full orientation control of the gripper and object is achieved through smooth orientation representation. Our approach has reasonable training durations and provides the option to include desired prior knowledge. The effectiveness and adaptability of the framework to different scenarios is demonstrated in simulated experiments.

Structure-Preserving Learning Using Gaussian Processes and Variational Integrators

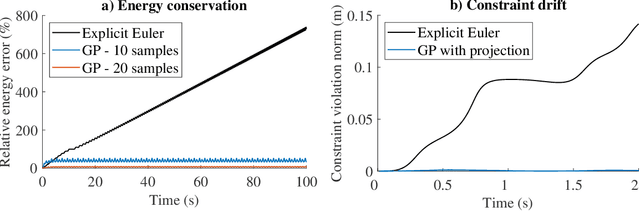
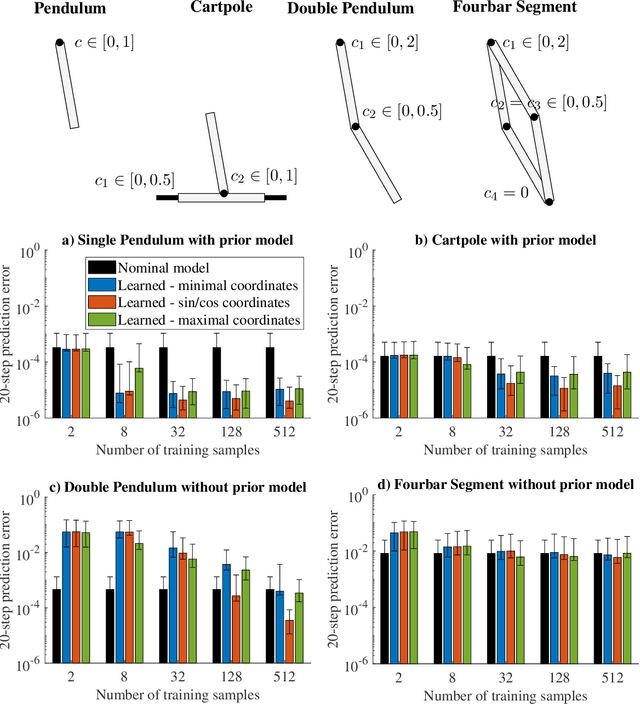
Gaussian process regression is often applied for learning unknown systems and specifying the uncertainty of the learned model. When using Gaussian process regression to learn unknown systems, a commonly considered approach consists of learning the residual dynamics after applying some standard discretization, which might however not be appropriate for the system at hand. Variational integrators are a less common yet promising approach to discretization, as they retain physical properties of the underlying system, such as energy conservation or satisfaction of explicit constraints. In this work, we propose the combination of a variational integrator for the nominal dynamics of a mechanical system and learning residual dynamics with Gaussian process regression. We extend our approach to systems with known kinematic constraints and provide formal bounds on the prediction uncertainty. The simulative evaluation of the proposed method shows desirable energy conservation properties in accordance with the theoretical results and demonstrates the capability of treating constrained dynamical systems.