Jan Brüdigam
Kernel-Based Optimal Control: An Infinitesimal Generator Approach
Dec 02, 2024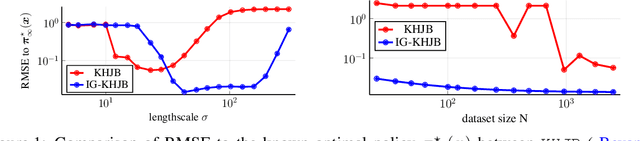

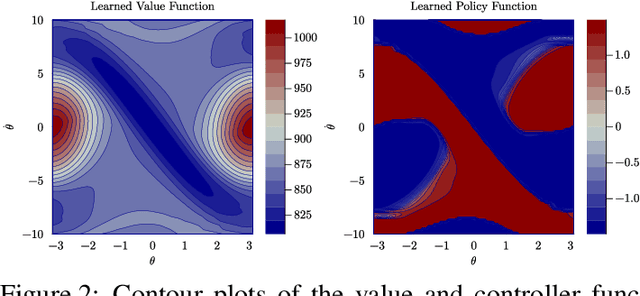
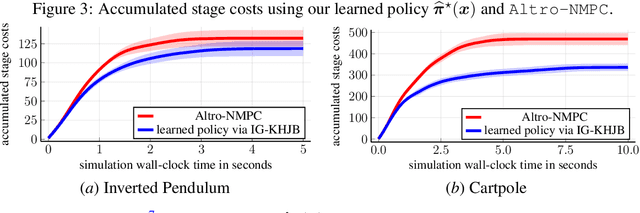
Abstract:This paper presents a novel approach for optimal control of nonlinear stochastic systems using infinitesimal generator learning within infinite-dimensional reproducing kernel Hilbert spaces. Our learning framework leverages data samples of system dynamics and stage cost functions, with only control penalties and constraints provided. The proposed method directly learns the diffusion operator of a controlled Fokker-Planck-Kolmogorov equation in an infinite-dimensional hypothesis space. This operator models the continuous-time evolution of the probability measure of the control system's state. We demonstrate that this approach seamlessly integrates with modern convex operator-theoretic Hamilton-Jacobi-Bellman recursions, enabling a data-driven solution to the optimal control problem. Furthermore, our statistical learning framework includes nonparametric estimators for uncontrolled forward infinitesimal generators as a special case. Numerical experiments, ranging from synthetic differential equations to simulated robotic systems, showcase the advantages of our approach compared to both modern data-driven and classical nonlinear programming methods for optimal control.
Reinforcement Learning with Lie Group Orientations for Robotics
Sep 18, 2024



Abstract:Handling orientations of robots and objects is a crucial aspect of many applications. Yet, ever so often, there is a lack of mathematical correctness when dealing with orientations, especially in learning pipelines involving, for example, artificial neural networks. In this paper, we investigate reinforcement learning with orientations and propose a simple modification of the network's input and output that adheres to the Lie group structure of orientations. As a result, we obtain an easy and efficient implementation that is directly usable with existing learning libraries and achieves significantly better performance than other common orientation representations. We briefly introduce Lie theory specifically for orientations in robotics to motivate and outline our approach. Subsequently, a thorough empirical evaluation of different combinations of orientation representations for states and actions demonstrates the superior performance of our proposed approach in different scenarios, including: direct orientation control, end effector orientation control, and pick-and-place tasks.
Jacta: A Versatile Planner for Learning Dexterous and Whole-body Manipulation
Aug 02, 2024Abstract:Robotic manipulation is challenging due to discontinuous dynamics, as well as high-dimensional state and action spaces. Data-driven approaches that succeed in manipulation tasks require large amounts of data and expert demonstrations, typically from humans. Existing manipulation planners are restricted to specific systems and often depend on specialized algorithms for using demonstration. Therefore, we introduce a flexible motion planner tailored to dexterous and whole-body manipulation tasks. Our planner creates readily usable demonstrations for reinforcement learning algorithms, eliminating the need for additional training pipeline complexities. With this approach, we can efficiently learn policies for complex manipulation tasks, where traditional reinforcement learning alone only makes little progress. Furthermore, we demonstrate that learned policies are transferable to real robotic systems for solving complex dexterous manipulation tasks.
Variational Integrators and Graph-Based Solvers for Multibody Dynamics in Maximal Coordinates
Feb 12, 2023



Abstract:Multibody dynamics simulators are an important tool in many fields, including learning and control for robotics. However, many existing dynamics simulators suffer from inaccuracies when dealing with constrained mechanical systems due to unsuitable integrators and dissatisfying constraint handling. Variational integrators are numerical discretization methods that can reduce physical inaccuracies when simulating mechanical systems, and formulating the dynamics in maximal coordinates allows for easy and numerically robust incorporation of constraints such as kinematic loops or contacts. Therefore, this article derives a variational integrator for mechanical systems with equality and inequality constraints in maximal coordinates. Additionally, efficient graph-based sparsity-exploiting algorithms for solving the integrator are provided and implemented as an open-source simulator. The evaluation of the simulator shows the improved physical accuracy due to the variational integrator and the advantages of the sparse solvers, while application examples of a walking robot and an exoskeleton with explicit constraints demonstrate the necessity and capabilities of maximal coordinates.
Dext-Gen: Dexterous Grasping in Sparse Reward Environments with Full Orientation Control
Jun 28, 2022

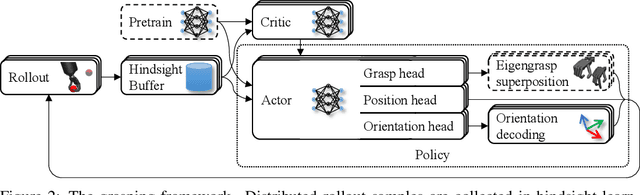
Abstract:Reinforcement learning is a promising method for robotic grasping as it can learn effective reaching and grasping policies in difficult scenarios. However, achieving human-like manipulation capabilities with sophisticated robotic hands is challenging because of the problem's high dimensionality. Although remedies such as reward shaping or expert demonstrations can be employed to overcome this issue, they often lead to oversimplified and biased policies. We present Dext-Gen, a reinforcement learning framework for Dexterous Grasping in sparse reward ENvironments that is applicable to a variety of grippers and learns unbiased and intricate policies. Full orientation control of the gripper and object is achieved through smooth orientation representation. Our approach has reasonable training durations and provides the option to include desired prior knowledge. The effectiveness and adaptability of the framework to different scenarios is demonstrated in simulated experiments.
Structure-Preserving Learning Using Gaussian Processes and Variational Integrators
Dec 10, 2021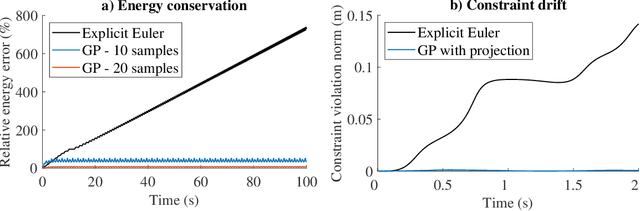
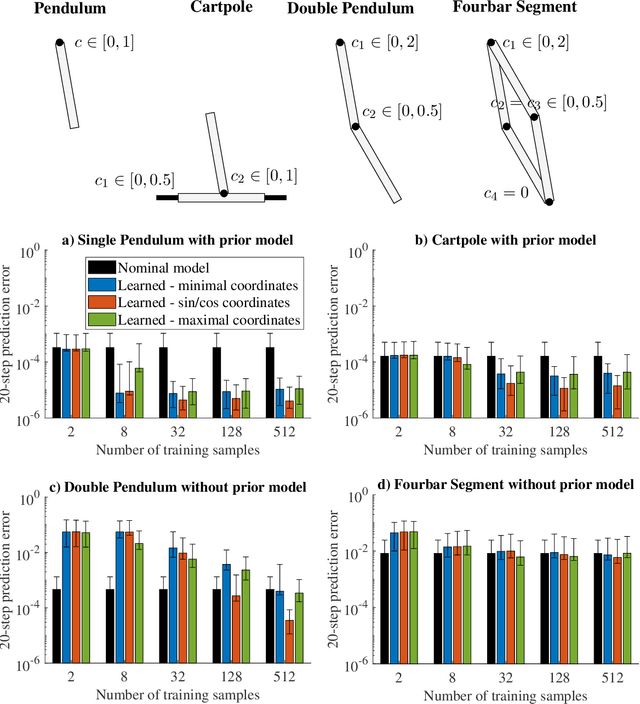
Abstract:Gaussian process regression is often applied for learning unknown systems and specifying the uncertainty of the learned model. When using Gaussian process regression to learn unknown systems, a commonly considered approach consists of learning the residual dynamics after applying some standard discretization, which might however not be appropriate for the system at hand. Variational integrators are a less common yet promising approach to discretization, as they retain physical properties of the underlying system, such as energy conservation or satisfaction of explicit constraints. In this work, we propose the combination of a variational integrator for the nominal dynamics of a mechanical system and learning residual dynamics with Gaussian process regression. We extend our approach to systems with known kinematic constraints and provide formal bounds on the prediction uncertainty. The simulative evaluation of the proposed method shows desirable energy conservation properties in accordance with the theoretical results and demonstrates the capability of treating constrained dynamical systems.
Linear-Time Contact and Friction Dynamics in Maximal Coordinates using Variational Integrators
Sep 15, 2021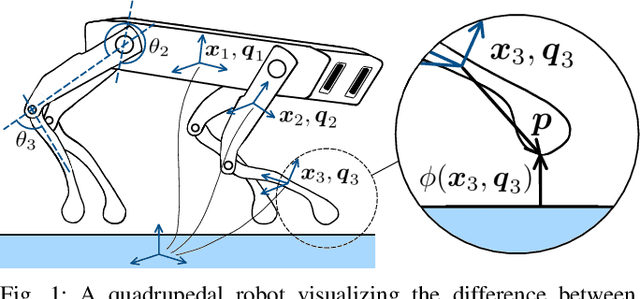
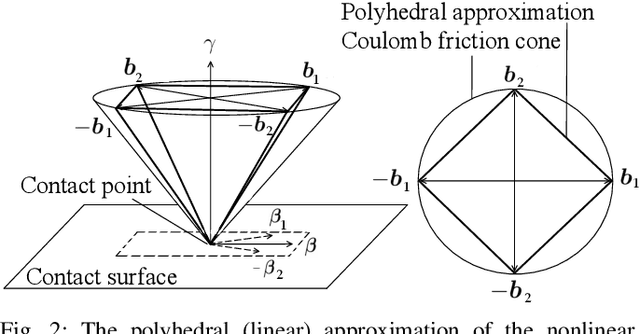
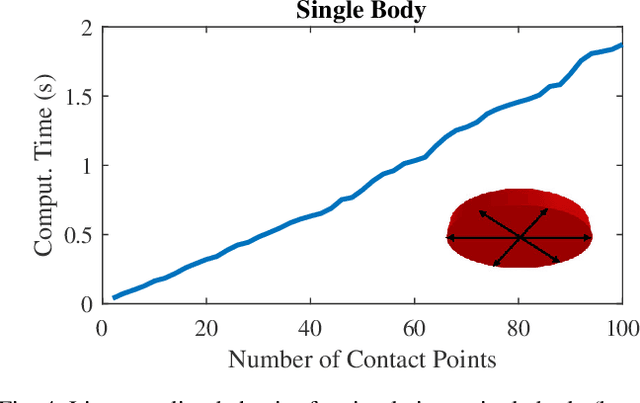
Abstract:Simulation of contact and friction dynamics is an important basis for control- and learning-based algorithms. However, the numerical difficulties of contact interactions pose a challenge for robust and efficient simulators. A maximal-coordinate representation of the dynamics enables efficient solving algorithms, but current methods in maximal coordinates require constraint stabilization schemes. Therefore, we propose an interior-point algorithm for the numerically robust treatment of rigid-body dynamics with contact interactions in maximal coordinates. Additionally, we discretize the dynamics with a variational integrator to prevent constraint drift. Our algorithm achieves linear-time complexity both in the number of contact points and the number of bodies, which is shown theoretically and demonstrated with an implementation. Furthermore, we simulate two robotic systems to highlight the applicability of the proposed algorithm.
Linear-Time Variational Integrators in Maximal Coordinates
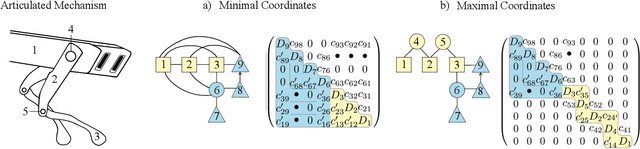
Feb 26, 2020
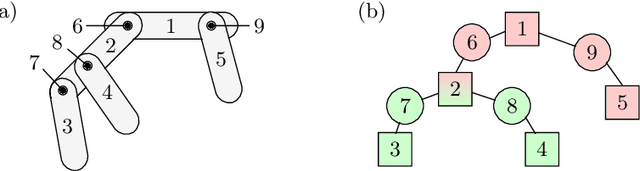
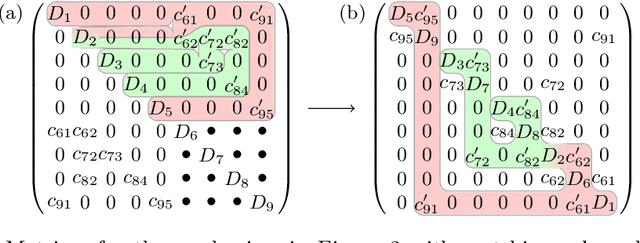
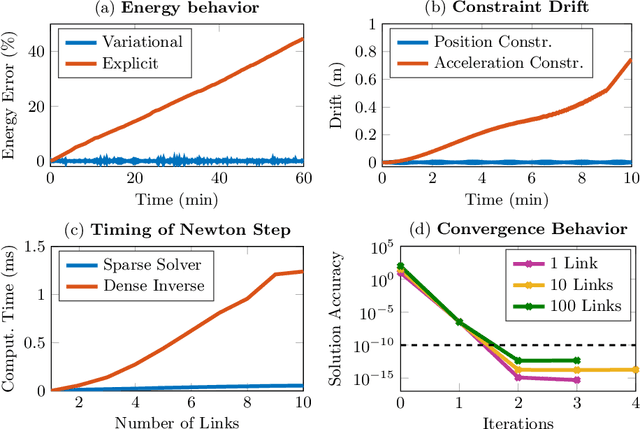
Abstract:Most dynamic simulation tools parameterize the configuration of multi-body robotic systems using minimal coordinates, also called generalized or joint coordinates. However, maximal-coordinate approaches have several advantages over minimal-coordinate parameterizations, including native handling of closed kinematic loops and nonholonomic constraints. This paper describes a linear-time variational integrator that is formulated in maximal coordinates. Due to its variational formulation, the algorithm does not suffer from constraint drift and has favorable energy and momentum conservation properties. A sparse matrix factorization technique allows the dynamics of a loop-free articulated mechanism with $n$ links to be computed in $O(n)$ (linear) time. Additional constraints that introduce loops can also be handled by the algorithm without incurring much computational overhead. Experimental results show that our approach offers speed competitive with state-of-the-art minimal-coordinate algorithms while outperforming them in several scenarios, especially when dealing with closed loops and configuration singularities.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge