Linear-Time Variational Integrators in Maximal Coordinates
Paper and Code
Feb 26, 2020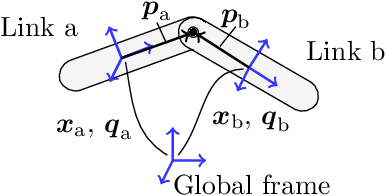
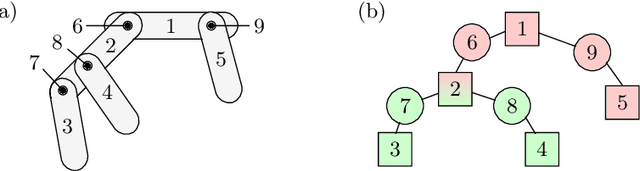
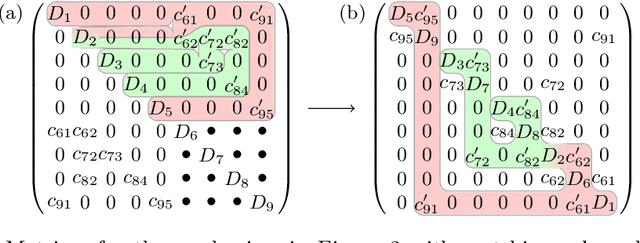
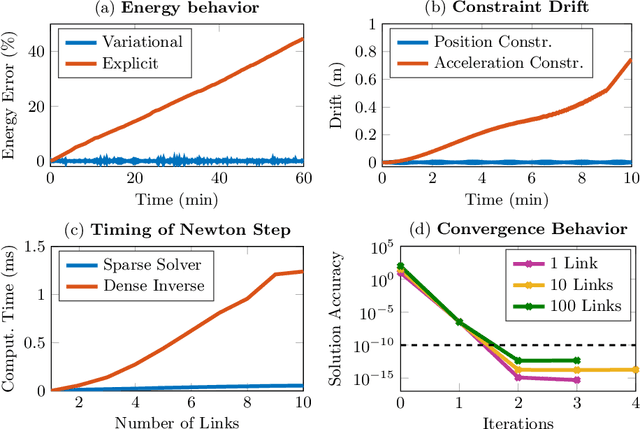
Most dynamic simulation tools parameterize the configuration of multi-body robotic systems using minimal coordinates, also called generalized or joint coordinates. However, maximal-coordinate approaches have several advantages over minimal-coordinate parameterizations, including native handling of closed kinematic loops and nonholonomic constraints. This paper describes a linear-time variational integrator that is formulated in maximal coordinates. Due to its variational formulation, the algorithm does not suffer from constraint drift and has favorable energy and momentum conservation properties. A sparse matrix factorization technique allows the dynamics of a loop-free articulated mechanism with $n$ links to be computed in $O(n)$ (linear) time. Additional constraints that introduce loops can also be handled by the algorithm without incurring much computational overhead. Experimental results show that our approach offers speed competitive with state-of-the-art minimal-coordinate algorithms while outperforming them in several scenarios, especially when dealing with closed loops and configuration singularities.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge