Petar Bevanda
Operator Models for Continuous-Time Offline Reinforcement Learning
Nov 13, 2025Abstract:Continuous-time stochastic processes underlie many natural and engineered systems. In healthcare, autonomous driving, and industrial control, direct interaction with the environment is often unsafe or impractical, motivating offline reinforcement learning from historical data. However, there is limited statistical understanding of the approximation errors inherent in learning policies from offline datasets. We address this by linking reinforcement learning to the Hamilton-Jacobi-Bellman equation and proposing an operator-theoretic algorithm based on a simple dynamic programming recursion. Specifically, we represent our world model in terms of the infinitesimal generator of controlled diffusion processes learned in a reproducing kernel Hilbert space. By integrating statistical learning methods and operator theory, we establish global convergence of the value function and derive finite-sample guarantees with bounds tied to system properties such as smoothness and stability. Our theoretical and numerical results indicate that operator-based approaches may hold promise in solving offline reinforcement learning using continuous-time optimal control.
Koopman-Equivariant Gaussian Processes
Feb 10, 2025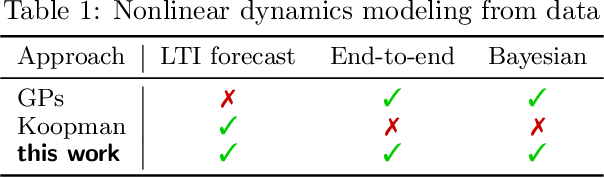
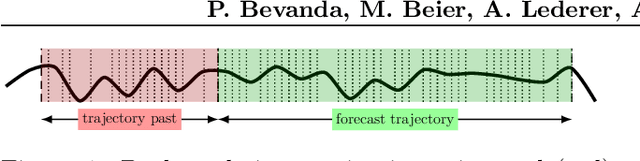

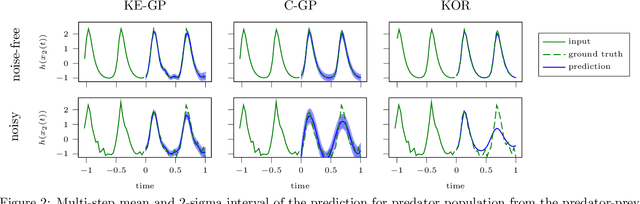
Abstract:Credible forecasting and representation learning of dynamical systems are of ever-increasing importance for reliable decision-making. To that end, we propose a family of Gaussian processes (GP) for dynamical systems with linear time-invariant responses, which are nonlinear only in initial conditions. This linearity allows us to tractably quantify forecasting and representational uncertainty, simultaneously alleviating the challenge of computing the distribution of trajectories from a GP-based dynamical system and enabling a new probabilistic treatment of learning Koopman operator representations. Using a trajectory-based equivariance -- which we refer to as \textit{Koopman equivariance} -- we obtain a GP model with enhanced generalization capabilities. To allow for large-scale regression, we equip our framework with variational inference based on suitable inducing points. Experiments demonstrate on-par and often better forecasting performance compared to kernel-based methods for learning dynamical systems.
Kernel-Based Optimal Control: An Infinitesimal Generator Approach
Dec 02, 2024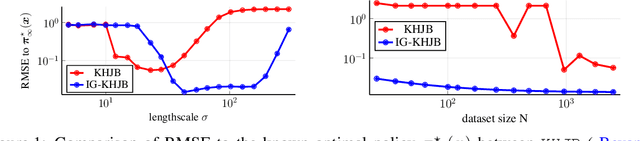

Abstract:This paper presents a novel approach for optimal control of nonlinear stochastic systems using infinitesimal generator learning within infinite-dimensional reproducing kernel Hilbert spaces. Our learning framework leverages data samples of system dynamics and stage cost functions, with only control penalties and constraints provided. The proposed method directly learns the diffusion operator of a controlled Fokker-Planck-Kolmogorov equation in an infinite-dimensional hypothesis space. This operator models the continuous-time evolution of the probability measure of the control system's state. We demonstrate that this approach seamlessly integrates with modern convex operator-theoretic Hamilton-Jacobi-Bellman recursions, enabling a data-driven solution to the optimal control problem. Furthermore, our statistical learning framework includes nonparametric estimators for uncontrolled forward infinitesimal generators as a special case. Numerical experiments, ranging from synthetic differential equations to simulated robotic systems, showcase the advantages of our approach compared to both modern data-driven and classical nonlinear programming methods for optimal control.
Data-Driven Optimal Feedback Laws via Kernel Mean Embeddings
Jul 23, 2024Abstract:This paper proposes a fully data-driven approach for optimal control of nonlinear control-affine systems represented by a stochastic diffusion. The focus is on the scenario where both the nonlinear dynamics and stage cost functions are unknown, while only control penalty function and constraints are provided. Leveraging the theory of reproducing kernel Hilbert spaces, we introduce novel kernel mean embeddings (KMEs) to identify the Markov transition operators associated with controlled diffusion processes. The KME learning approach seamlessly integrates with modern convex operator-theoretic Hamilton-Jacobi-Bellman recursions. Thus, unlike traditional dynamic programming methods, our approach exploits the ``kernel trick'' to break the curse of dimensionality. We demonstrate the effectiveness of our method through numerical examples, highlighting its ability to solve a large class of nonlinear optimal control problems.
Nonparametric Control-Koopman Operator Learning: Flexible and Scalable Models for Prediction and Control
May 12, 2024Abstract:Linearity of Koopman operators and simplicity of their estimators coupled with model-reduction capabilities has lead to their great popularity in applications for learning dynamical systems. While nonparametric Koopman operator learning in infinite-dimensional reproducing kernel Hilbert spaces is well understood for autonomous systems, its control system analogues are largely unexplored. Addressing systems with control inputs in a principled manner is crucial for fully data-driven learning of controllers, especially since existing approaches commonly resort to representational heuristics or parametric models of limited expressiveness and scalability. We address the aforementioned challenge by proposing a universal framework via control-affine reproducing kernels that enables direct estimation of a single operator even for control systems. The proposed approach, called control-Koopman operator regression (cKOR), is thus completely analogous to Koopman operator regression of the autonomous case. First in the literature, we present a nonparametric framework for learning Koopman operator representations of nonlinear control-affine systems that does not suffer from the curse of control input dimensionality. This allows for reformulating the infinite-dimensional learning problem in a finite-dimensional space based solely on data without apriori loss of precision due to a restriction to a finite span of functions or inputs as in other approaches. For enabling applications to large-scale control systems, we also enhance the scalability of control-Koopman operator estimators by leveraging random projections (sketching). The efficacy of our novel cKOR approach is demonstrated on both forecasting and control tasks.
Koopman Kernel Regression
May 25, 2023

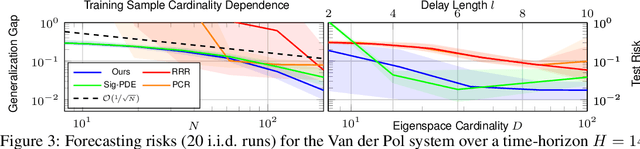
Abstract:Many machine learning approaches for decision making, such as reinforcement learning, rely on simulators or predictive models to forecast the time-evolution of quantities of interest, e.g., the state of an agent or the reward of a policy. Forecasts of such complex phenomena are commonly described by highly nonlinear dynamical systems, making their use in optimization-based decision-making challenging. Koopman operator theory offers a beneficial paradigm for addressing this problem by characterizing forecasts via linear dynamical systems. This makes system analysis and long-term predictions simple -- involving only matrix multiplications. However, the transformation to a linear system is generally non-trivial and unknown, requiring learning-based approaches. While there exists a variety of approaches, they usually lack crucial learning-theoretic guarantees, such that the behavior of the obtained models with increasing data and dimensionality is often unclear. We address the aforementioned by deriving a novel reproducing kernel Hilbert space (RKHS) that solely spans transformations into linear dynamical systems. The resulting Koopman Kernel Regression (KKR) framework enables the use of statistical learning tools from function approximation for novel convergence results and generalization risk bounds under weaker assumptions than existing work. Our numerical experiments indicate advantages over state-of-the-art statistical learning approaches for Koopman-based predictors.
Towards Data-driven LQR with KoopmanizingFlows
Jan 27, 2022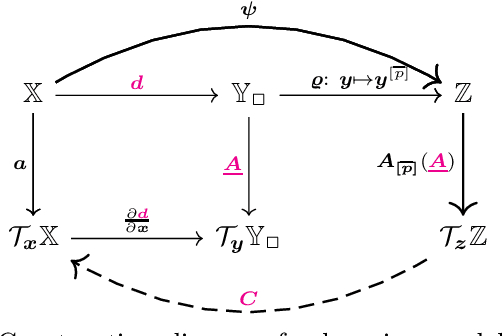
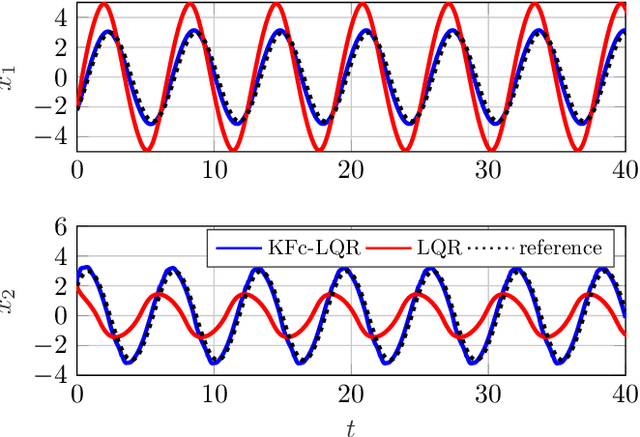
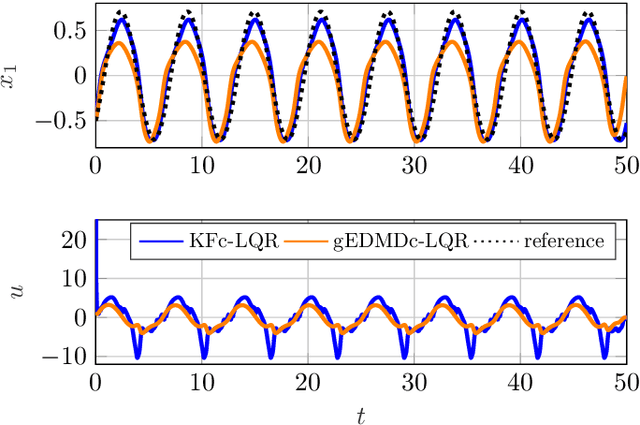
Abstract:We propose a novel framework for learning linear time-invariant (LTI) models for a class of continuous-time non-autonomous nonlinear dynamics based on a representation of Koopman operators. In general, the operator is infinite-dimensional but, crucially, linear. To utilize it for efficient LTI control, we learn a finite representation of the Koopman operator that is linear in controls while concurrently learning meaningful lifting coordinates. For the latter, we rely on KoopmanizingFlows - a diffeomorphism-based representation of Koopman operators. With such a learned model, we can replace the nonlinear infinite-horizon optimal control problem with quadratic costs to that of a linear quadratic regulator (LQR), facilitating efficacious optimal control for nonlinear systems. The prediction and control efficacy of the proposed method is verified on simulation examples.
KoopmanizingFlows: Diffeomorphically Learning Stable Koopman Operators
Dec 08, 2021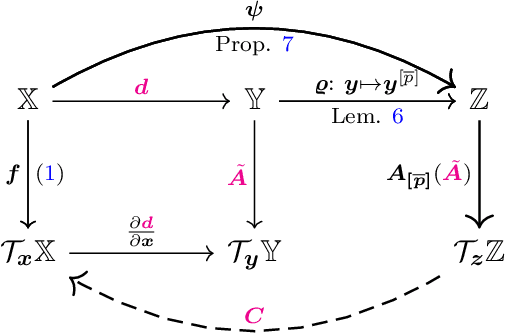

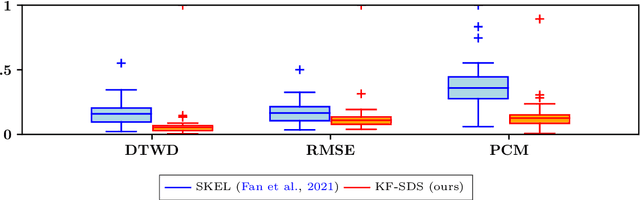

Abstract:We propose a novel framework for constructing linear time-invariant (LTI) models for data-driven representations of the Koopman operator for a class of stable nonlinear dynamics. The Koopman operator (generator) lifts a finite-dimensional nonlinear system to a possibly infinite-dimensional linear feature space. To utilize it for modeling, one needs to discover finite-dimensional representations of the Koopman operator. Learning suitable features is challenging, as one needs to learn LTI features that are both Koopman-invariant (evolve linearly under the dynamics) as well as relevant (spanning the original state) - a generally unsupervised learning task. For a theoretically well-founded solution to this problem, we propose learning Koopman-invariant coordinates by composing a diffeomorphic learner with a lifted aggregate system of a latent linear model. Using an unconstrained parameterization of stable matrices along with the aforementioned feature construction, we learn the Koopman operator features without assuming a predefined library of functions or knowing the spectrum, while ensuring stability regardless of the operator approximation accuracy. We demonstrate the superior efficacy of the proposed method in comparison to a state-of-the-art method on the well-known LASA handwriting dataset.
Learning the Koopman Eigendecomposition: A Diffeomorphic Approach
Oct 15, 2021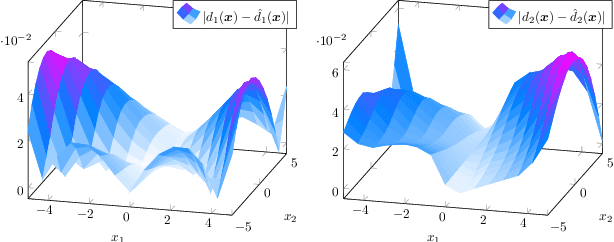
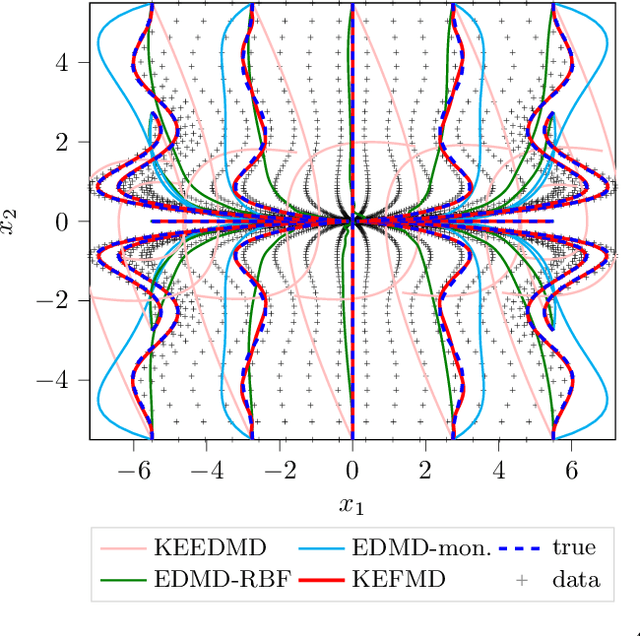

Abstract:We present a novel data-driven approach for learning linear representations of a class of stable nonlinear systems using Koopman eigenfunctions. By learning the conjugacy map between a nonlinear system and its Jacobian linearization through a Normalizing Flow one can guarantee the learned function is a diffeomorphism. Using this diffeomorphism, we construct eigenfunctions of the nonlinear system via the spectral equivalence of conjugate systems - allowing the construction of linear predictors for nonlinear systems. The universality of the diffeomorphism learner leads to the universal approximation of the nonlinear system's Koopman eigenfunctions. The developed method is also safe as it guarantees the model is asymptotically stable regardless of the representation accuracy. To our best knowledge, this is the first work to close the gap between the operator, system and learning theories. The efficacy of our approach is shown through simulation examples.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge