Nonparametric Control-Koopman Operator Learning: Flexible and Scalable Models for Prediction and Control

Linearity of Koopman operators and simplicity of their estimators coupled with model-reduction capabilities has lead to their great popularity in applications for learning dynamical systems. While nonparametric Koopman operator learning in infinite-dimensional reproducing kernel Hilbert spaces is well understood for autonomous systems, its control system analogues are largely unexplored. Addressing systems with control inputs in a principled manner is crucial for fully data-driven learning of controllers, especially since existing approaches commonly resort to representational heuristics or parametric models of limited expressiveness and scalability. We address the aforementioned challenge by proposing a universal framework via control-affine reproducing kernels that enables direct estimation of a single operator even for control systems. The proposed approach, called control-Koopman operator regression (cKOR), is thus completely analogous to Koopman operator regression of the autonomous case. First in the literature, we present a nonparametric framework for learning Koopman operator representations of nonlinear control-affine systems that does not suffer from the curse of control input dimensionality. This allows for reformulating the infinite-dimensional learning problem in a finite-dimensional space based solely on data without apriori loss of precision due to a restriction to a finite span of functions or inputs as in other approaches. For enabling applications to large-scale control systems, we also enhance the scalability of control-Koopman operator estimators by leveraging random projections (sketching). The efficacy of our novel cKOR approach is demonstrated on both forecasting and control tasks.

Curve Trajectory Model for Human Preferred Path Planning of Automated Vehicles

Automated driving systems are often used for lane keeping tasks. By these systems, a local path is planned ahead of the vehicle. However, these paths are often found unnatural by human drivers. We propose a linear driver model, which can calculate node points that reflect the preferences of human drivers and based on these node points a human driver preferred motion path can be designed for autonomous driving. The model input is the road curvature. We apply this model to a self-developed Euler-curve-based curve fitting algorithm. Through a case study, we show that the model based planned path can reproduce the average behavior of human curve path selection. We analyze the performance of the proposed model through statistical analysis that shows the validity of the captured relations.

Non-linear State-space Model Identification from Video Data using Deep Encoders

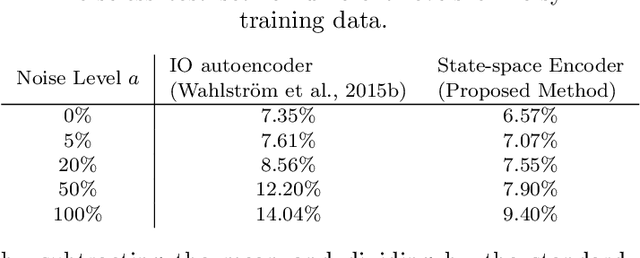
Identifying systems with high-dimensional inputs and outputs, such as systems measured by video streams, is a challenging problem with numerous applications in robotics, autonomous vehicles and medical imaging. In this paper, we propose a novel non-linear state-space identification method starting from high-dimensional input and output data. Multiple computational and conceptual advances are combined to handle the high-dimensional nature of the data. An encoder function, represented by a neural network, is introduced to learn a reconstructability map to estimate the model states from past inputs and outputs. This encoder function is jointly learned with the dynamics. Furthermore, multiple computational improvements, such as an improved reformulation of multiple shooting and batch optimization, are proposed to keep the computational time under control when dealing with high-dimensional and large datasets. We apply the proposed method to a video stream of a simulated environment of a controllable ball in a unit box. The simulation study shows low simulation error with excellent long term prediction for the obtained model using the proposed method.

Nonlinear state-space identification using deep encoder networks

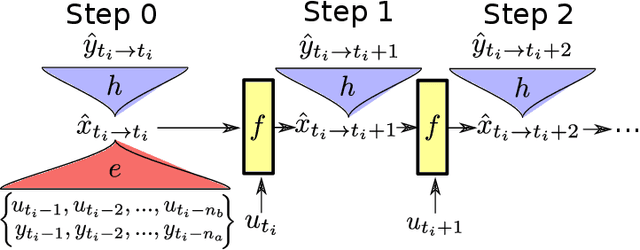
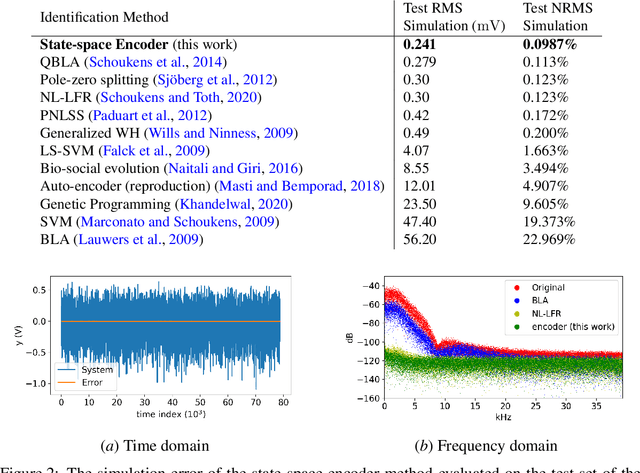
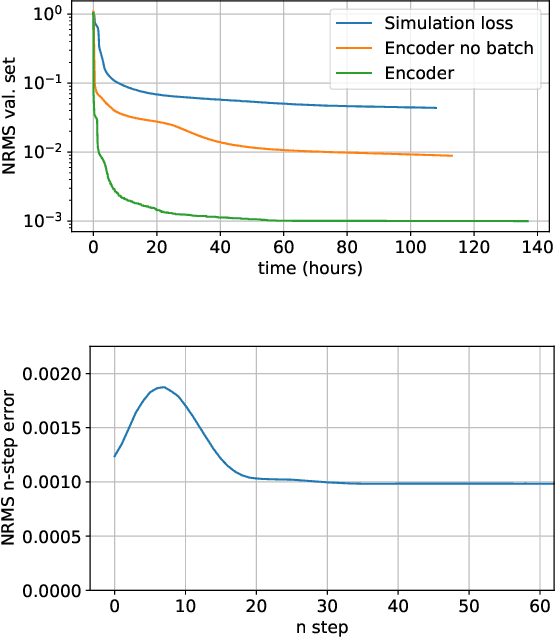
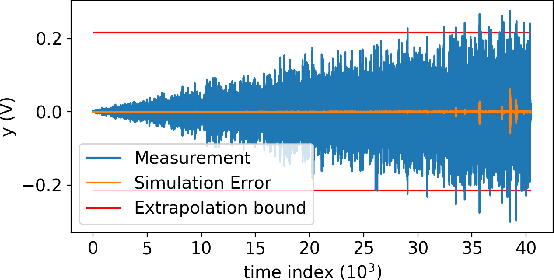
Nonlinear state-space identification for dynamical systems is most often performed by minimizing the simulation error to reduce the effect of model errors. This optimization problem becomes computationally expensive for large datasets. Moreover, the problem is also strongly non-convex, often leading to sub-optimal parameter estimates. This paper introduces a method that approximates the simulation loss by splitting the data set into multiple independent sections similar to the multiple shooting method. This splitting operation allows for the use of stochastic gradient optimization methods which scale well with data set size and has a smoothing effect on the non-convex cost function. The main contribution of this paper is the introduction of an encoder function to estimate the initial state at the start of each section. The encoder function estimates the initial states using a feed-forward neural network starting from historical input and output samples. The efficiency and performance of the proposed state-space encoder method is illustrated on two well-known benchmarks where, for instance, the method achieves the lowest known simulation error on the Wiener--Hammerstein benchmark.