Nonlinear state-space identification using deep encoder networks

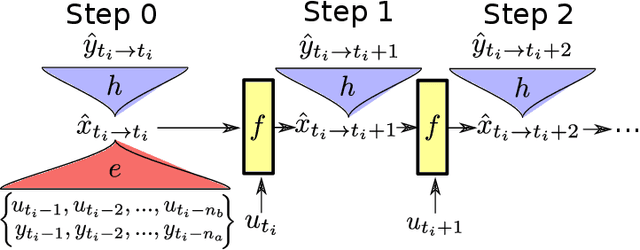
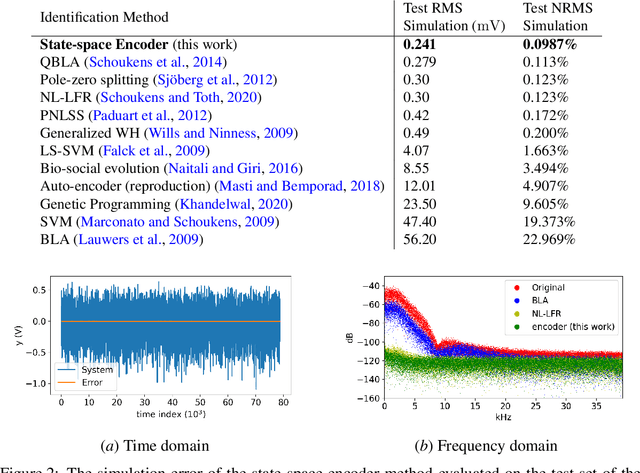
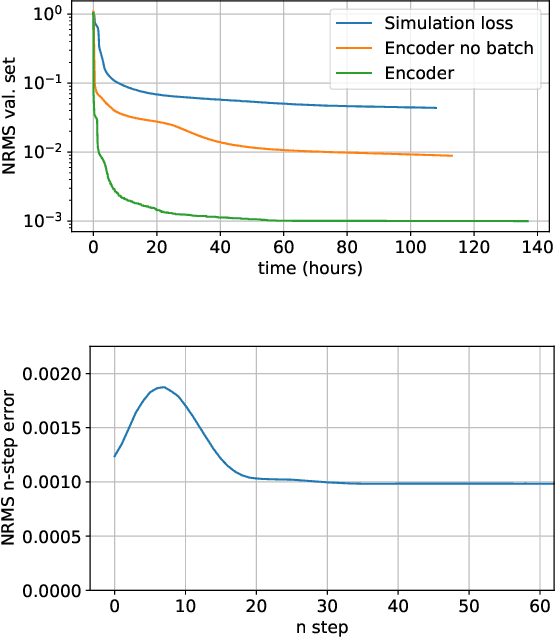
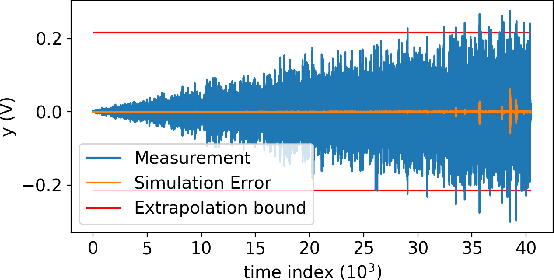
Nonlinear state-space identification for dynamical systems is most often performed by minimizing the simulation error to reduce the effect of model errors. This optimization problem becomes computationally expensive for large datasets. Moreover, the problem is also strongly non-convex, often leading to sub-optimal parameter estimates. This paper introduces a method that approximates the simulation loss by splitting the data set into multiple independent sections similar to the multiple shooting method. This splitting operation allows for the use of stochastic gradient optimization methods which scale well with data set size and has a smoothing effect on the non-convex cost function. The main contribution of this paper is the introduction of an encoder function to estimate the initial state at the start of each section. The encoder function estimates the initial states using a feed-forward neural network starting from historical input and output samples. The efficiency and performance of the proposed state-space encoder method is illustrated on two well-known benchmarks where, for instance, the method achieves the lowest known simulation error on the Wiener--Hammerstein benchmark.

Controlling Rayleigh-Bénard convection via Reinforcement Learning

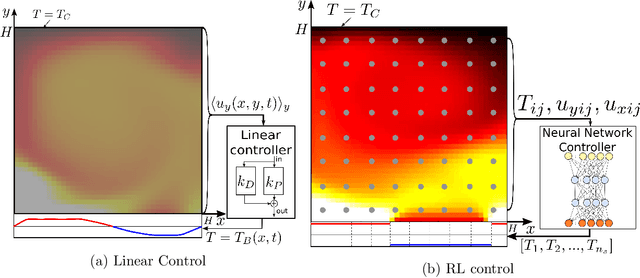
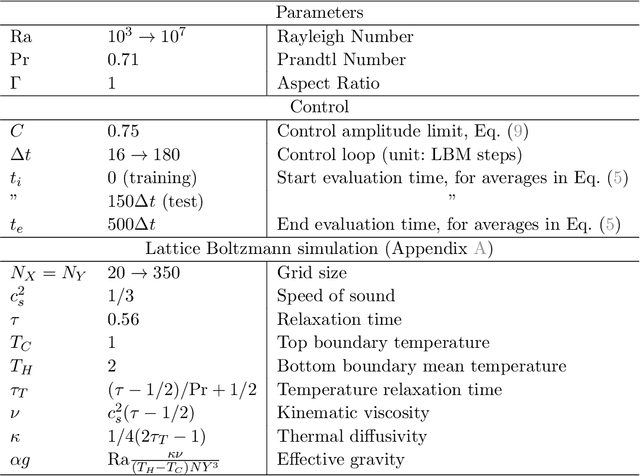
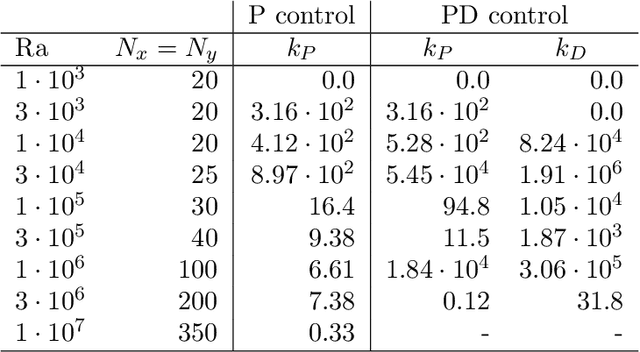
Thermal convection is ubiquitous in nature as well as in many industrial applications. The identification of effective control strategies to, e.g., suppress or enhance the convective heat exchange under fixed external thermal gradients is an outstanding fundamental and technological issue. In this work, we explore a novel approach, based on a state-of-the-art Reinforcement Learning (RL) algorithm, which is capable of significantly reducing the heat transport in a two-dimensional Rayleigh-B\'enard system by applying small temperature fluctuations to the lower boundary of the system. By using numerical simulations, we show that our RL-based control is able to stabilize the conductive regime and bring the onset of convection up to a Rayleigh number $Ra_c \approx 3 \cdot 10^4$, whereas in the uncontrolled case it holds $Ra_{c}=1708$. Additionally, for $Ra > 3 \cdot 10^4$, our approach outperforms other state-of-the-art control algorithms reducing the heat flux by a factor of about $2.5$. In the last part of the manuscript, we address theoretical limits connected to controlling an unstable and chaotic dynamics as the one considered here. We show that controllability is hindered by observability and/or capabilities of actuating actions, which can be quantified in terms of characteristic time delays. When these delays become comparable with the Lyapunov time of the system, control becomes impossible.