Synthetic Lagrangian Turbulence by Generative Diffusion Models

Lagrangian turbulence lies at the core of numerous applied and fundamental problems related to the physics of dispersion and mixing in engineering, bio-fluids, atmosphere, oceans, and astrophysics. Despite exceptional theoretical, numerical, and experimental efforts conducted over the past thirty years, no existing models are capable of faithfully reproducing statistical and topological properties exhibited by particle trajectories in turbulence. We propose a machine learning approach, based on a state-of-the-art Diffusion Model, to generate single-particle trajectories in three-dimensional turbulence at high Reynolds numbers, thereby bypassing the need for direct numerical simulations or experiments to obtain reliable Lagrangian data. Our model demonstrates the ability to quantitatively reproduce all relevant statistical benchmarks over the entire range of time scales, including the presence of fat tails distribution for the velocity increments, anomalous power law, and enhancement of intermittency around the dissipative scale. The model exhibits good generalizability for extreme events, achieving unprecedented intensity and rarity. This paves the way for producing synthetic high-quality datasets for pre-training various downstream applications of Lagrangian turbulence.

Reconstructing Rayleigh-Benard flows out of temperature-only measurements using Physics-Informed Neural Networks

We investigate the capabilities of Physics-Informed Neural Networks (PINNs) to reconstruct turbulent Rayleigh-Benard flows using only temperature information. We perform a quantitative analysis of the quality of the reconstructions at various amounts of low-passed-filtered information and turbulent intensities. We compare our results with those obtained via nudging, a classical equation-informed data assimilation technique. At low Rayleigh numbers, PINNs are able to reconstruct with high precision, comparable to the one achieved with nudging. At high Rayleigh numbers, PINNs outperform nudging and are able to achieve satisfactory reconstruction of the velocity fields only when data for temperature is provided with high spatial and temporal density. When data becomes sparse, the PINNs performance worsens, not only in a point-to-point error sense but also, and contrary to nudging, in a statistical sense, as can be seen in the probability density functions and energy spectra.

Generative Adversarial Networks to infer velocity components in rotating turbulent flows

Inference problems for two-dimensional snapshots of rotating turbulent flows are studied. We perform a systematic quantitative benchmark of point-wise and statistical reconstruction capabilities of the linear Extended Proper Orthogonal Decomposition (EPOD) method, a non-linear Convolutional Neural Network (CNN) and a Generative Adversarial Network (GAN). We attack the important task of inferring one velocity component out of the measurement of a second one, and two cases are studied: (I) both components lay in the plane orthogonal to the rotation axis and (II) one of the two is parallel to the rotation axis. We show that EPOD method works well only for the former case where both components are strongly correlated, while CNN and GAN always outperform EPOD both concerning point-wise and statistical reconstructions. For case (II), when the input and output data are weakly correlated, all methods fail to reconstruct faithfully the point-wise information. In this case, only GAN is able to reconstruct the field in a statistical sense. The analysis is performed using both standard validation tools based on L2 spatial distance between the prediction and the ground truth and more sophisticated multi-scale analysis using wavelet decomposition. Statistical validation is based on standard Jensen-Shannon divergence between the probability density functions, spectral properties and multi-scale flatness.

Taming Lagrangian Chaos with Multi-Objective Reinforcement Learning

We consider the problem of two active particles in 2D complex flows with the multi-objective goals of minimizing both the dispersion rate and the energy consumption of the pair. We approach the problem by means of Multi Objective Reinforcement Learning (MORL), combining scalarization techniques together with a Q-learning algorithm, for Lagrangian drifters that have variable swimming velocity. We show that MORL is able to find a set of trade-off solutions forming an optimal Pareto frontier. As a benchmark, we show that a set of heuristic strategies are dominated by the MORL solutions. We consider the situation in which the agents cannot update their control variables continuously, but only after a discrete (decision) time, $\tau$. We show that there is a range of decision times, in between the Lyapunov time and the continuous updating limit, where Reinforcement Learning finds strategies that significantly improve over heuristics. In particular, we discuss how large decision times require enhanced knowledge of the flow, whereas for smaller $\tau$ all a priori heuristic strategies become Pareto optimal.

Inferring Turbulent Parameters via Machine Learning

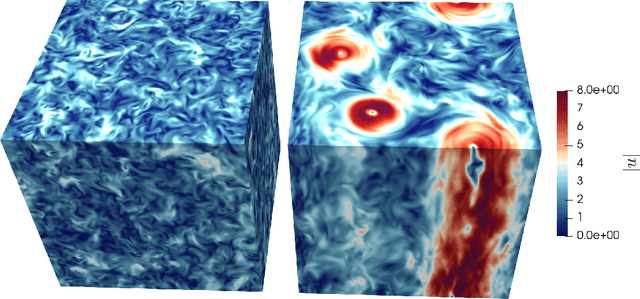
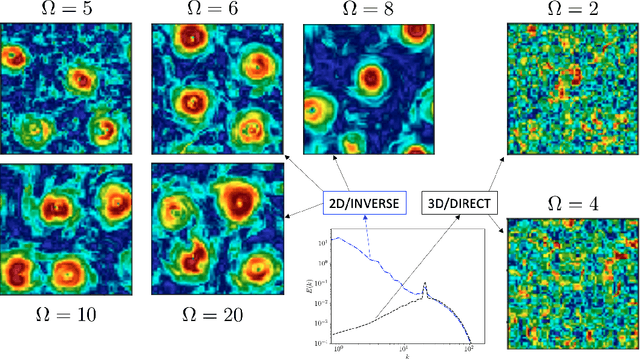
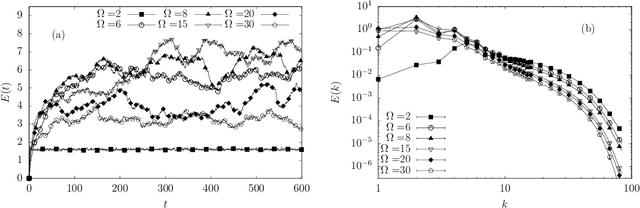
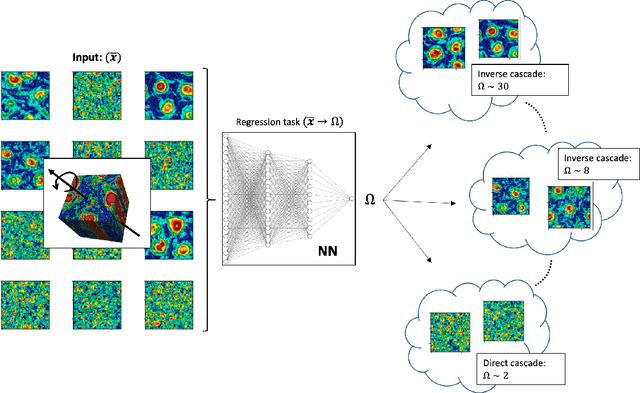
We design a machine learning technique to solve the general problem of inferring physical parameters from the observation of turbulent flows, a relevant exercise in many theoretical and applied fields, from engineering to earth observation and astrophysics. Our approach is to train the machine learning system to regress the rotation frequency of the flow's reference frame, from the observation of the flow's velocity amplitude on a 2d plane extracted from the 3d domain. The machine learning approach consists of a Deep Convolutional Neural Network (DCNN) of the same kind developed in computer vision. The training and validation datasets are produced by means of fully resolved direct numerical simulations. This study shows interesting results from two different points of view. From the machine learning point of view it shows the potential of DCNN, reaching good results on such a particularly complex problem that goes well outside the limits of human vision. Second, from the physics point of view, it provides an example on how machine learning can be exploited in data analysis to infer information that would be inaccessible otherwise. Indeed, by comparing DCNN with the other possible Bayesian approaches, we find that DCNN yields to a much higher inference accuracy in all the examined cases.

Reinforcement learning for pursuit and evasion of microswimmers at low Reynolds number

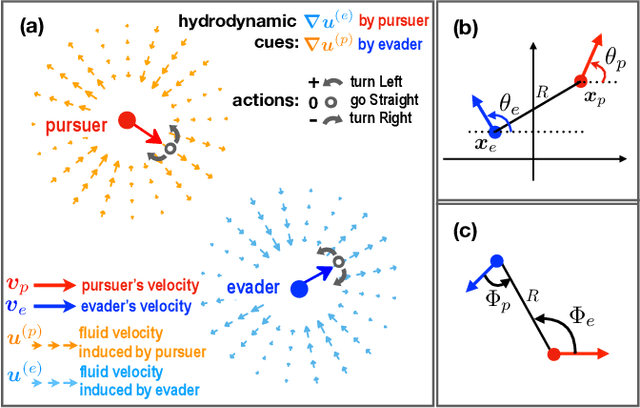
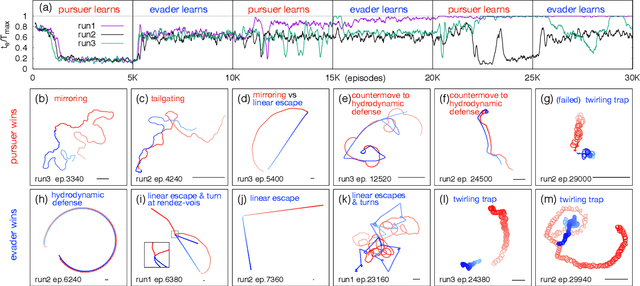
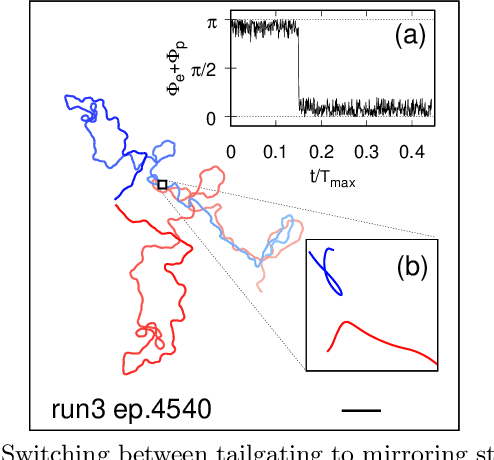
Aquatic organisms can use hydrodynamic cues to navigate, find their preys and escape from predators. We consider a model of two competing microswimmers engaged in a pursue-evasion task while immersed in a low-Reynolds-number environment. The players have limited abilities: they can only sense hydrodynamic disturbances, which provide some cue about the opponent's position, and perform simple manoeuvres. The goal of the pursuer is to capturethe evader in the shortest possible time. Conversely the evader aims at deferring capture as much as possible. We show that by means of Reinforcement Learning the players find efficient and physically explainable strategies which non-trivially exploit the hydrodynamic environment. This Letter offers a proof-of-concept for the use of Reinforcement Learning to discover prey-predator strategies in aquatic environments, with potential applications to underwater robotics.

Optimal control of point-to-point navigation in turbulent time-dependent flows using Reinforcement Learning

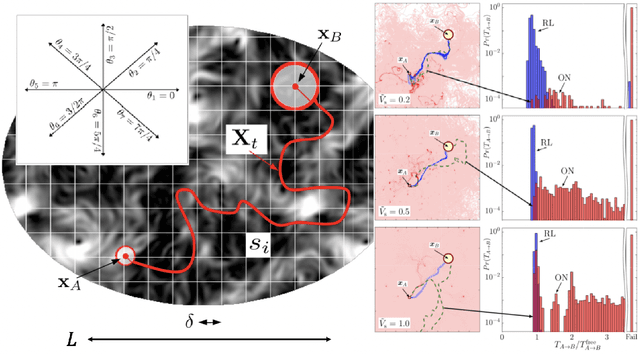
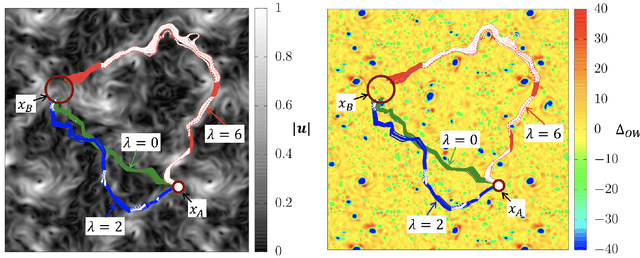
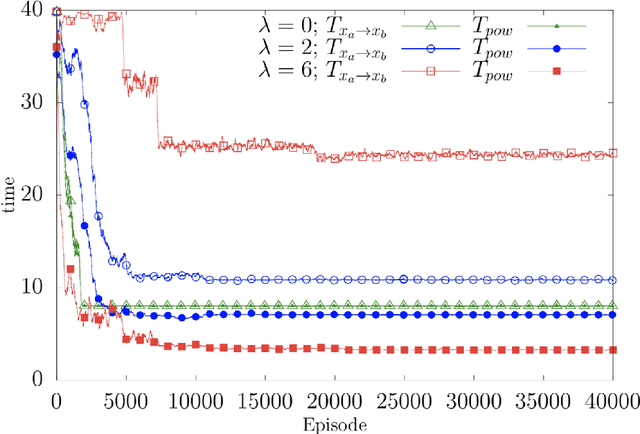
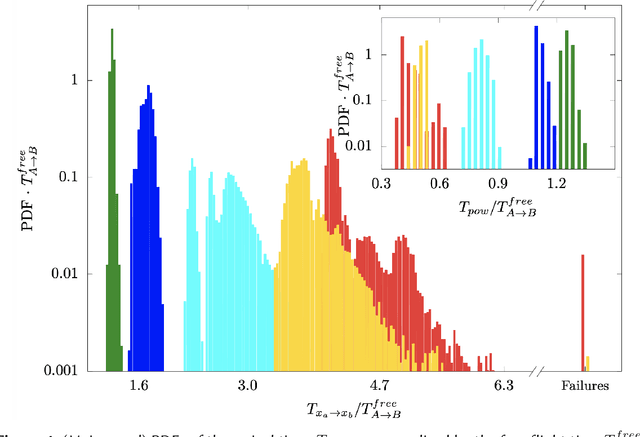
We present theoretical and numerical results concerning the problem to find the path that minimizes the time to navigate between two given points in a complex fluid under realistic navigation constraints. We contrast deterministic Optimal Navigation (ON) control with stochastic policies obtained by Reinforcement Learning (RL) algorithms. We show that Actor-Critic RL algorithms are able to find quasi-optimal solutions in the presence of either time-independent or chaotically evolving flow configurations. For our application, ON solutions develop unstable behavior within the typical duration of the navigation process, and are therefore not useful in practice. We first explore navigation of turbulent flow using a constant propulsion speed. Based on a discretized phase-space, the propulsion direction is adjusted with the aim to minimize the time spent to reach the target. Further, we explore a case where additional control is obtained by allowing the engine to power off. Exploiting advection of the underlying flow, allows the target to be reached with less energy consumption. In this case, we optimize a linear combination between the total navigation time and the total time the engine is switched off. Our approach can be generalized to other setups, for example, navigation under imperfect environmental forecast or with different models for the moving vessel.

Controlling Rayleigh-Bénard convection via Reinforcement Learning

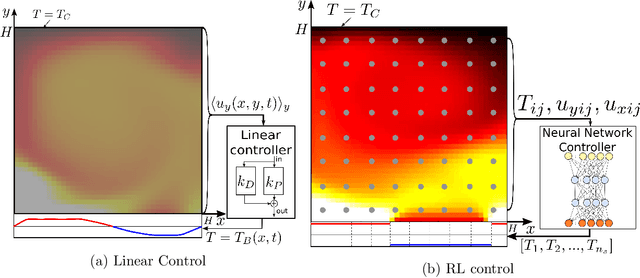
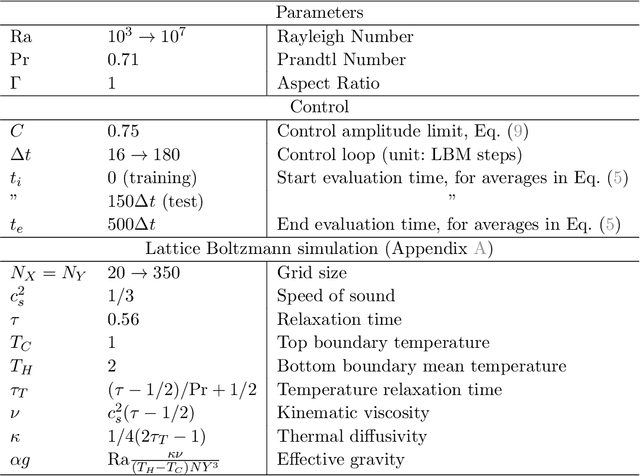
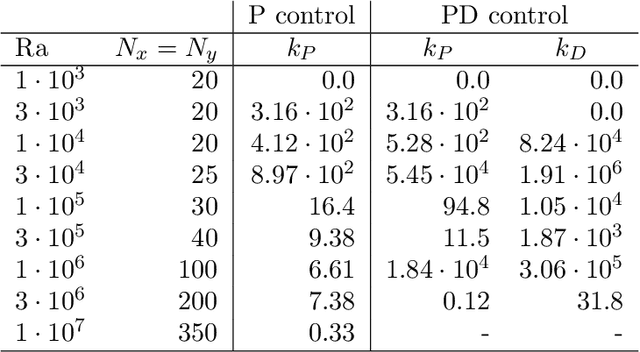
Thermal convection is ubiquitous in nature as well as in many industrial applications. The identification of effective control strategies to, e.g., suppress or enhance the convective heat exchange under fixed external thermal gradients is an outstanding fundamental and technological issue. In this work, we explore a novel approach, based on a state-of-the-art Reinforcement Learning (RL) algorithm, which is capable of significantly reducing the heat transport in a two-dimensional Rayleigh-B\'enard system by applying small temperature fluctuations to the lower boundary of the system. By using numerical simulations, we show that our RL-based control is able to stabilize the conductive regime and bring the onset of convection up to a Rayleigh number $Ra_c \approx 3 \cdot 10^4$, whereas in the uncontrolled case it holds $Ra_{c}=1708$. Additionally, for $Ra > 3 \cdot 10^4$, our approach outperforms other state-of-the-art control algorithms reducing the heat flux by a factor of about $2.5$. In the last part of the manuscript, we address theoretical limits connected to controlling an unstable and chaotic dynamics as the one considered here. We show that controllability is hindered by observability and/or capabilities of actuating actions, which can be quantified in terms of characteristic time delays. When these delays become comparable with the Lyapunov time of the system, control becomes impossible.

Zermelo's problem: Optimal point-to-point navigation in 2D turbulent flows using Reinforcement Learning

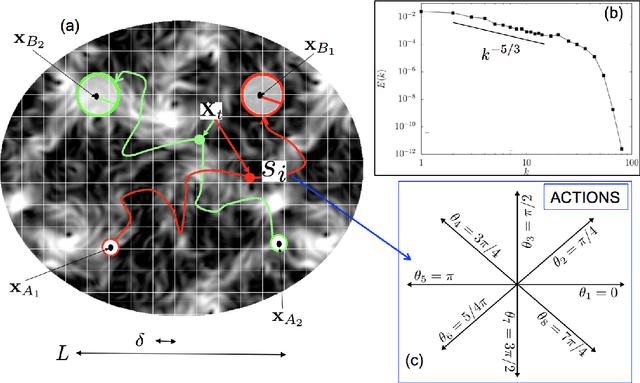
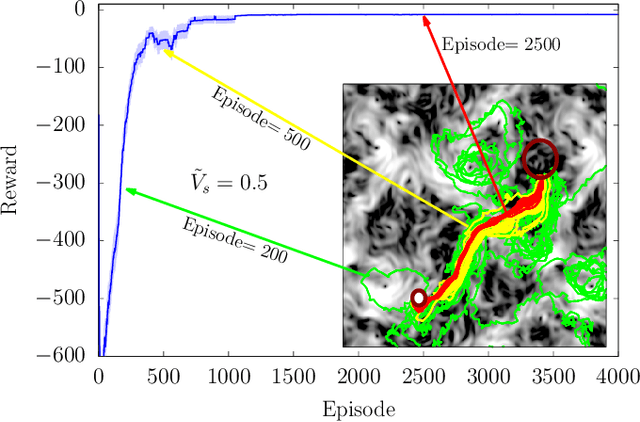
To find the path that minimizes the time to navigate between two given points in a fluid flow is known as the Zermelo's problem. Here, we investigate it by using a Reinforcement Learning (RL) approach for the case of a vessel which has a slip velocity with fixed intensity, V_s, but variable direction and navigating in a 2D turbulent sea. We use an Actor-Critic RL algorithm, and compare the results with strategies obtained analytically from continuous Optimal Navigation (ON) protocols. We show that for our application, ON solutions are unstable for the typical duration of the navigation process, and are therefore not useful in practice. On the other hand, RL solutions are much more robust with respect to small changes in the initial conditions and to external noise, and are able to find optimal trajectories even when V_s is much smaller than the maximum flow velocity. Furthermore, we show how the RL approach is able to take advantage of the flow properties in order to reach the target, especially when the steering speed is small.

Flow Navigation by Smart Microswimmers via Reinforcement Learning

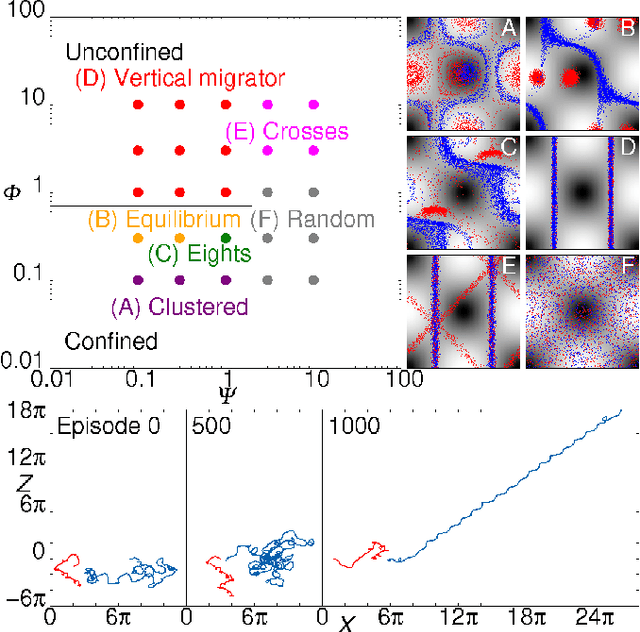
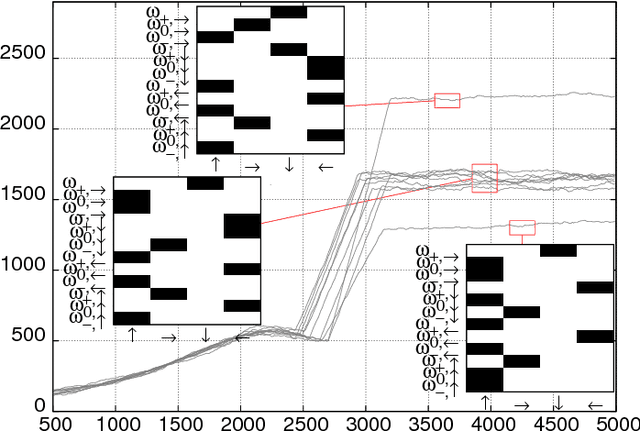
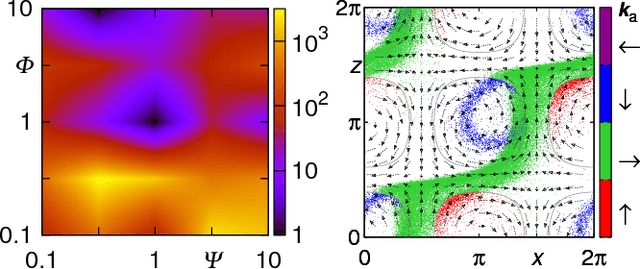
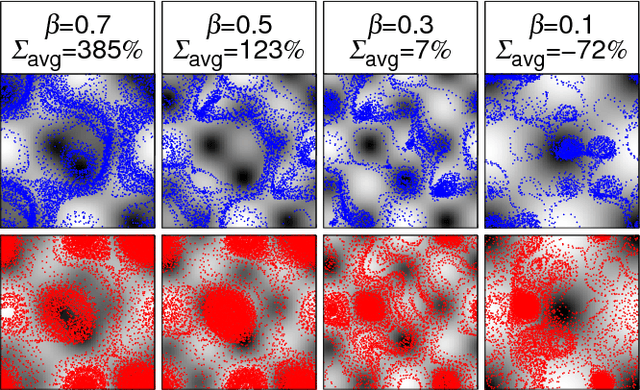
Smart active particles can acquire some limited knowledge of the fluid environment from simple mechanical cues and exert a control on their preferred steering direction. Their goal is to learn the best way to navigate by exploiting the underlying flow whenever possible. As an example, we focus our attention on smart gravitactic swimmers. These are active particles whose task is to reach the highest altitude within some time horizon, given the constraints enforced by fluid mechanics. By means of numerical experiments, we show that swimmers indeed learn nearly optimal strategies just by experience. A reinforcement learning algorithm allows particles to learn effective strategies even in difficult situations when, in the absence of control, they would end up being trapped by flow structures. These strategies are highly nontrivial and cannot be easily guessed in advance. This Letter illustrates the potential of reinforcement learning algorithms to model adaptive behavior in complex flows and paves the way towards the engineering of smart microswimmers that solve difficult navigation problems.