Taming Lagrangian Chaos with Multi-Objective Reinforcement Learning

We consider the problem of two active particles in 2D complex flows with the multi-objective goals of minimizing both the dispersion rate and the energy consumption of the pair. We approach the problem by means of Multi Objective Reinforcement Learning (MORL), combining scalarization techniques together with a Q-learning algorithm, for Lagrangian drifters that have variable swimming velocity. We show that MORL is able to find a set of trade-off solutions forming an optimal Pareto frontier. As a benchmark, we show that a set of heuristic strategies are dominated by the MORL solutions. We consider the situation in which the agents cannot update their control variables continuously, but only after a discrete (decision) time, $\tau$. We show that there is a range of decision times, in between the Lyapunov time and the continuous updating limit, where Reinforcement Learning finds strategies that significantly improve over heuristics. In particular, we discuss how large decision times require enhanced knowledge of the flow, whereas for smaller $\tau$ all a priori heuristic strategies become Pareto optimal.

Reinforcement learning for pursuit and evasion of microswimmers at low Reynolds number

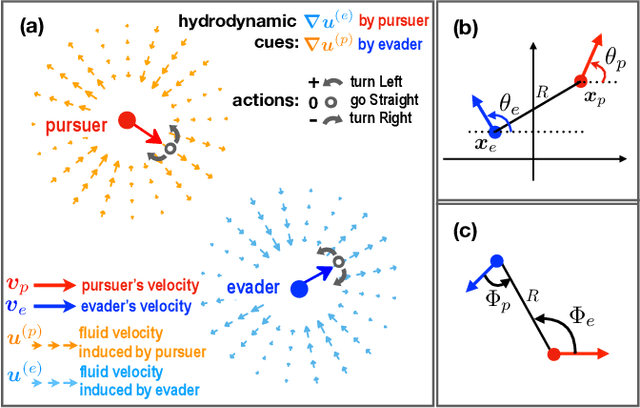
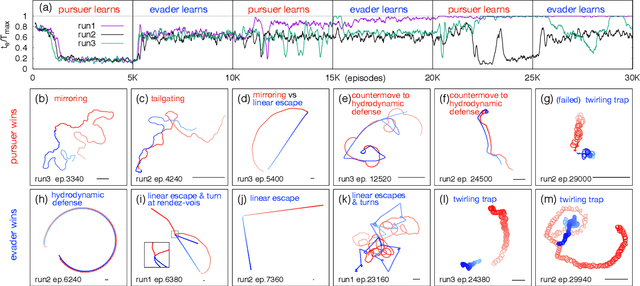
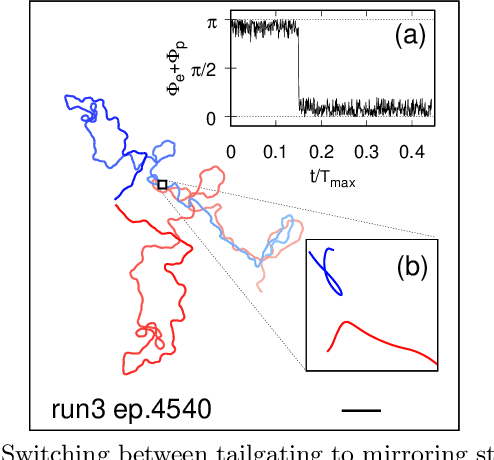
Aquatic organisms can use hydrodynamic cues to navigate, find their preys and escape from predators. We consider a model of two competing microswimmers engaged in a pursue-evasion task while immersed in a low-Reynolds-number environment. The players have limited abilities: they can only sense hydrodynamic disturbances, which provide some cue about the opponent's position, and perform simple manoeuvres. The goal of the pursuer is to capturethe evader in the shortest possible time. Conversely the evader aims at deferring capture as much as possible. We show that by means of Reinforcement Learning the players find efficient and physically explainable strategies which non-trivially exploit the hydrodynamic environment. This Letter offers a proof-of-concept for the use of Reinforcement Learning to discover prey-predator strategies in aquatic environments, with potential applications to underwater robotics.

Effective models and predictability of chaotic multiscale systems via machine learning

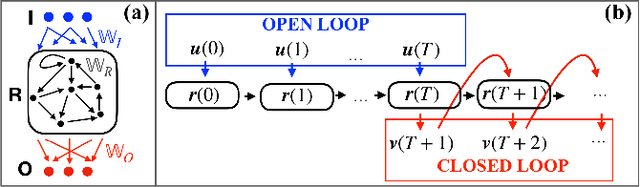
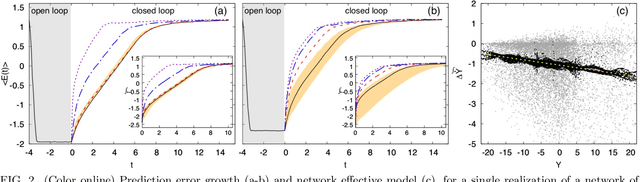
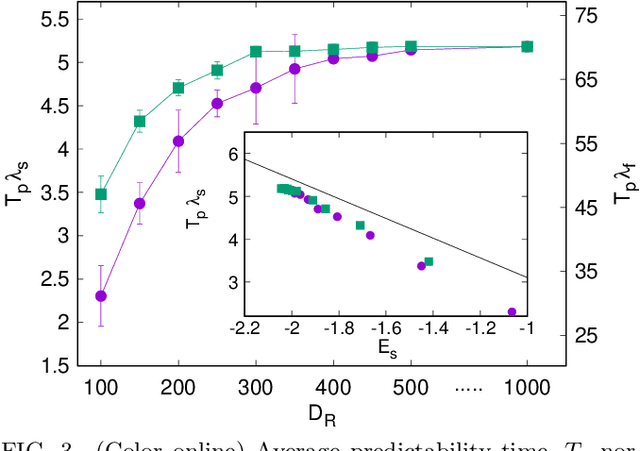
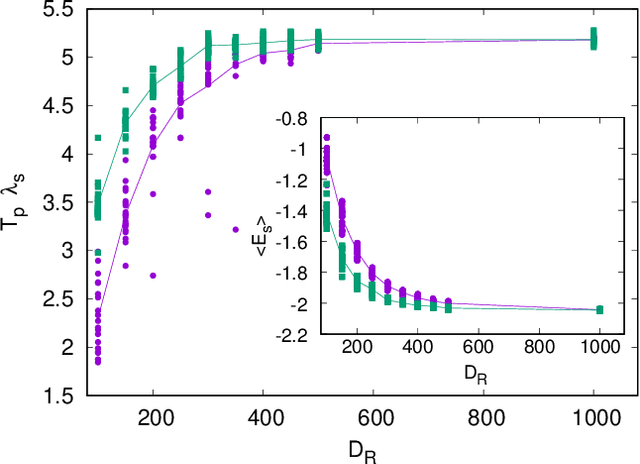
We scrutinize the use of machine learning, based on reservoir computing, to build data-driven effective models of multiscale chaotic systems. We show that, for a wide scale separation, machine learning generates effective models akin to those obtained using multiscale asymptotic techniques and, remarkably, remains effective in predictability also when the scale separation is reduced. We also show that predictability can be improved by hybridizing the reservoir with an imperfect model.