Optimal control of point-to-point navigation in turbulent time-dependent flows using Reinforcement Learning

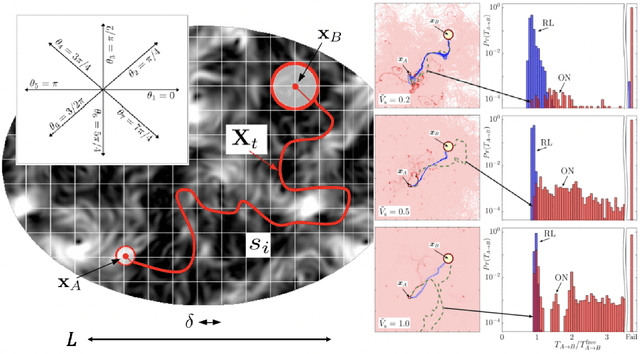
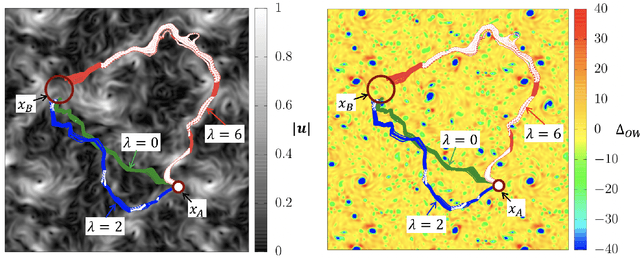
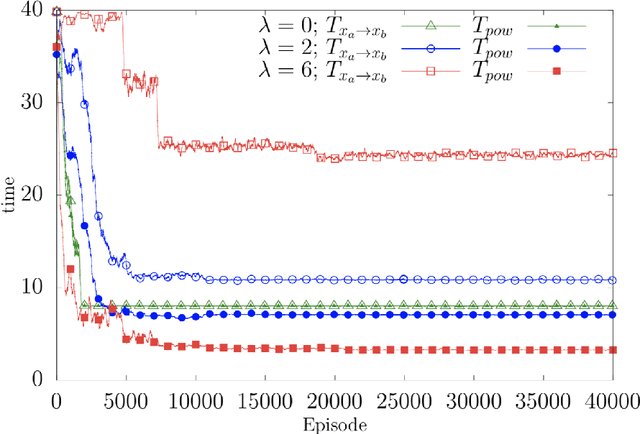
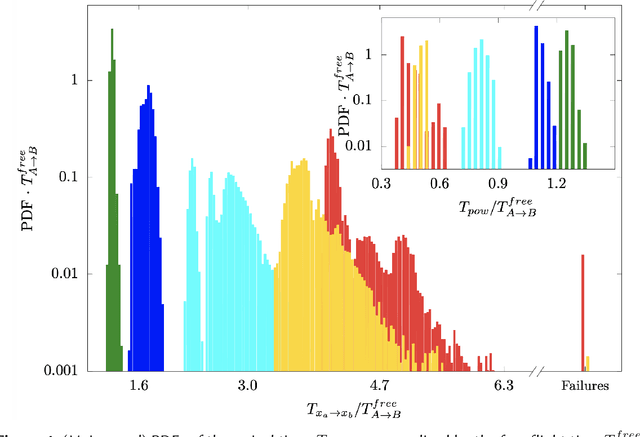
We present theoretical and numerical results concerning the problem to find the path that minimizes the time to navigate between two given points in a complex fluid under realistic navigation constraints. We contrast deterministic Optimal Navigation (ON) control with stochastic policies obtained by Reinforcement Learning (RL) algorithms. We show that Actor-Critic RL algorithms are able to find quasi-optimal solutions in the presence of either time-independent or chaotically evolving flow configurations. For our application, ON solutions develop unstable behavior within the typical duration of the navigation process, and are therefore not useful in practice. We first explore navigation of turbulent flow using a constant propulsion speed. Based on a discretized phase-space, the propulsion direction is adjusted with the aim to minimize the time spent to reach the target. Further, we explore a case where additional control is obtained by allowing the engine to power off. Exploiting advection of the underlying flow, allows the target to be reached with less energy consumption. In this case, we optimize a linear combination between the total navigation time and the total time the engine is switched off. Our approach can be generalized to other setups, for example, navigation under imperfect environmental forecast or with different models for the moving vessel.