Optimal control of point-to-point navigation in turbulent time-dependent flows using Reinforcement Learning

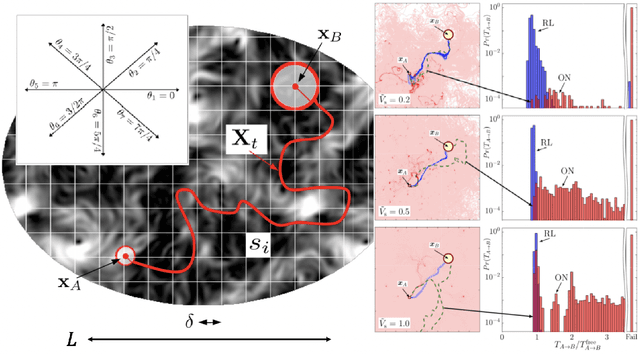
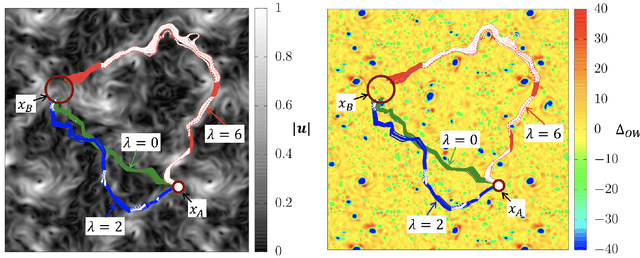
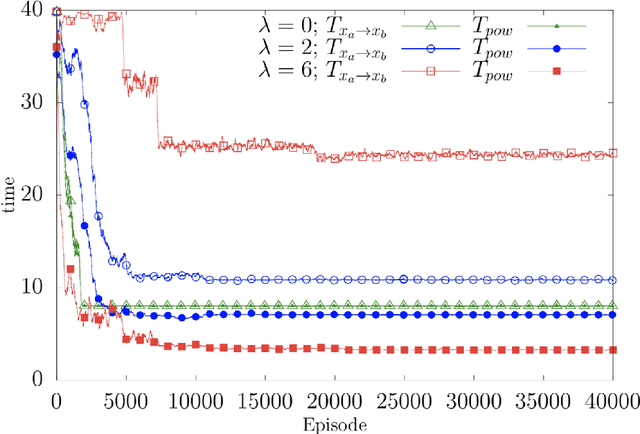
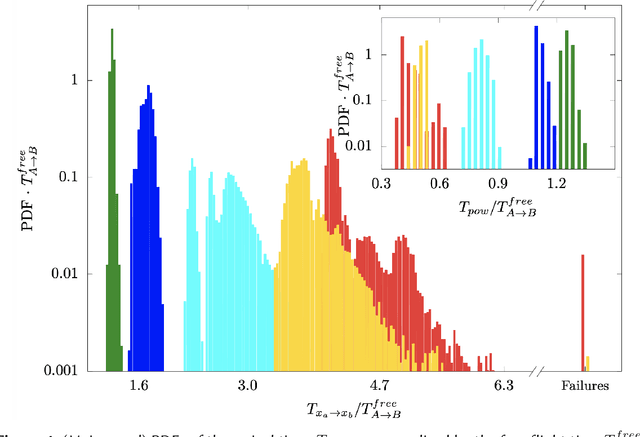
We present theoretical and numerical results concerning the problem to find the path that minimizes the time to navigate between two given points in a complex fluid under realistic navigation constraints. We contrast deterministic Optimal Navigation (ON) control with stochastic policies obtained by Reinforcement Learning (RL) algorithms. We show that Actor-Critic RL algorithms are able to find quasi-optimal solutions in the presence of either time-independent or chaotically evolving flow configurations. For our application, ON solutions develop unstable behavior within the typical duration of the navigation process, and are therefore not useful in practice. We first explore navigation of turbulent flow using a constant propulsion speed. Based on a discretized phase-space, the propulsion direction is adjusted with the aim to minimize the time spent to reach the target. Further, we explore a case where additional control is obtained by allowing the engine to power off. Exploiting advection of the underlying flow, allows the target to be reached with less energy consumption. In this case, we optimize a linear combination between the total navigation time and the total time the engine is switched off. Our approach can be generalized to other setups, for example, navigation under imperfect environmental forecast or with different models for the moving vessel.

Zermelo's problem: Optimal point-to-point navigation in 2D turbulent flows using Reinforcement Learning

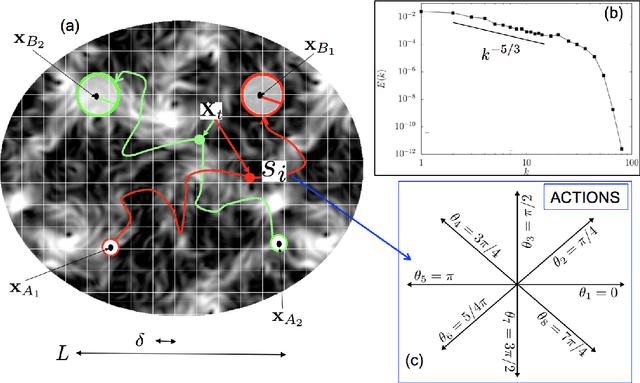
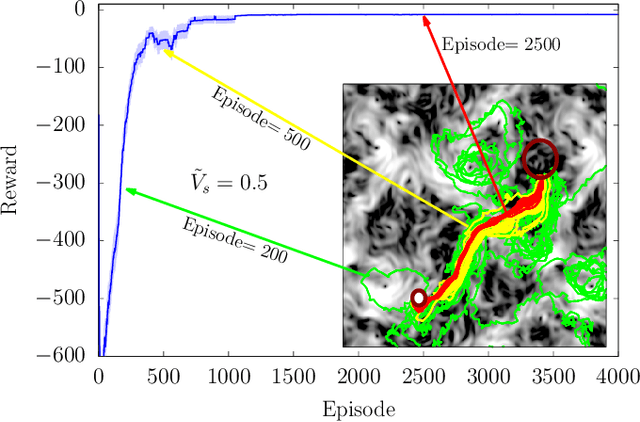
To find the path that minimizes the time to navigate between two given points in a fluid flow is known as the Zermelo's problem. Here, we investigate it by using a Reinforcement Learning (RL) approach for the case of a vessel which has a slip velocity with fixed intensity, V_s, but variable direction and navigating in a 2D turbulent sea. We use an Actor-Critic RL algorithm, and compare the results with strategies obtained analytically from continuous Optimal Navigation (ON) protocols. We show that for our application, ON solutions are unstable for the typical duration of the navigation process, and are therefore not useful in practice. On the other hand, RL solutions are much more robust with respect to small changes in the initial conditions and to external noise, and are able to find optimal trajectories even when V_s is much smaller than the maximum flow velocity. Furthermore, we show how the RL approach is able to take advantage of the flow properties in order to reach the target, especially when the steering speed is small.

Flow Navigation by Smart Microswimmers via Reinforcement Learning

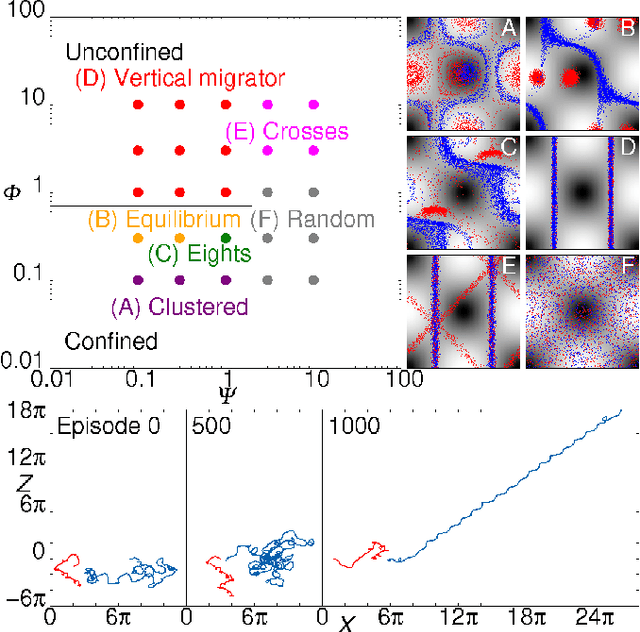
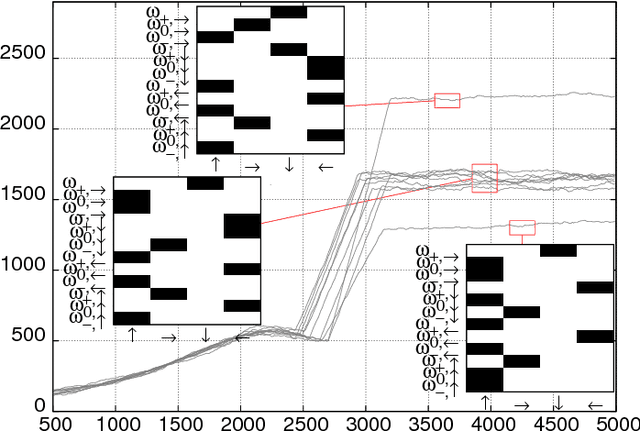
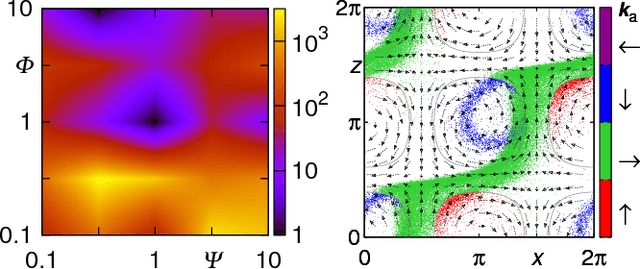
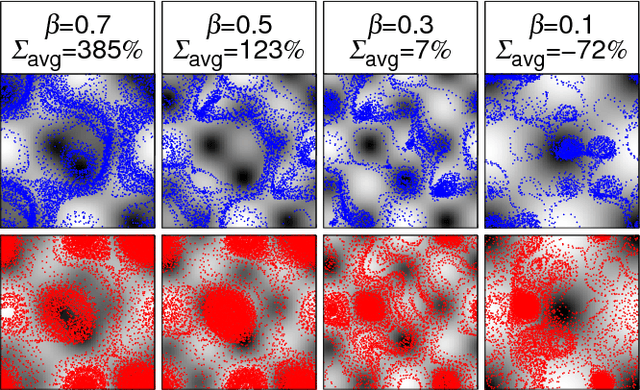
Smart active particles can acquire some limited knowledge of the fluid environment from simple mechanical cues and exert a control on their preferred steering direction. Their goal is to learn the best way to navigate by exploiting the underlying flow whenever possible. As an example, we focus our attention on smart gravitactic swimmers. These are active particles whose task is to reach the highest altitude within some time horizon, given the constraints enforced by fluid mechanics. By means of numerical experiments, we show that swimmers indeed learn nearly optimal strategies just by experience. A reinforcement learning algorithm allows particles to learn effective strategies even in difficult situations when, in the absence of control, they would end up being trapped by flow structures. These strategies are highly nontrivial and cannot be easily guessed in advance. This Letter illustrates the potential of reinforcement learning algorithms to model adaptive behavior in complex flows and paves the way towards the engineering of smart microswimmers that solve difficult navigation problems.