Zermelo's problem: Optimal point-to-point navigation in 2D turbulent flows using Reinforcement Learning

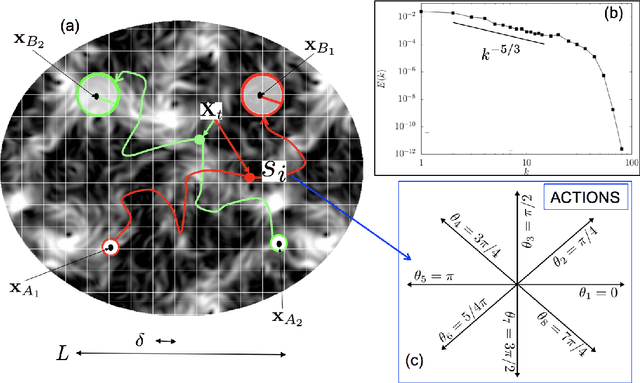
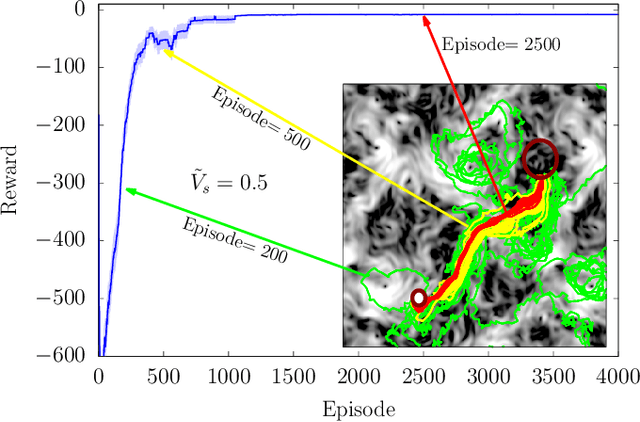
To find the path that minimizes the time to navigate between two given points in a fluid flow is known as the Zermelo's problem. Here, we investigate it by using a Reinforcement Learning (RL) approach for the case of a vessel which has a slip velocity with fixed intensity, V_s, but variable direction and navigating in a 2D turbulent sea. We use an Actor-Critic RL algorithm, and compare the results with strategies obtained analytically from continuous Optimal Navigation (ON) protocols. We show that for our application, ON solutions are unstable for the typical duration of the navigation process, and are therefore not useful in practice. On the other hand, RL solutions are much more robust with respect to small changes in the initial conditions and to external noise, and are able to find optimal trajectories even when V_s is much smaller than the maximum flow velocity. Furthermore, we show how the RL approach is able to take advantage of the flow properties in order to reach the target, especially when the steering speed is small.