Reconstructing Rayleigh-Benard flows out of temperature-only measurements using Physics-Informed Neural Networks

We investigate the capabilities of Physics-Informed Neural Networks (PINNs) to reconstruct turbulent Rayleigh-Benard flows using only temperature information. We perform a quantitative analysis of the quality of the reconstructions at various amounts of low-passed-filtered information and turbulent intensities. We compare our results with those obtained via nudging, a classical equation-informed data assimilation technique. At low Rayleigh numbers, PINNs are able to reconstruct with high precision, comparable to the one achieved with nudging. At high Rayleigh numbers, PINNs outperform nudging and are able to achieve satisfactory reconstruction of the velocity fields only when data for temperature is provided with high spatial and temporal density. When data becomes sparse, the PINNs performance worsens, not only in a point-to-point error sense but also, and contrary to nudging, in a statistical sense, as can be seen in the probability density functions and energy spectra.

Physics-informed neural network for ultrasound nondestructive quantification of surface breaking cracks

We introduce an optimized physics-informed neural network (PINN) trained to solve the problem of identifying and characterizing a surface breaking crack in a metal plate. PINNs are neural networks that can combine data and physics in the learning process by adding the residuals of a system of Partial Differential Equations to the loss function. Our PINN is supervised with realistic ultrasonic surface acoustic wave data acquired at a frequency of 5 MHz. The ultrasonic surface wave data is represented as a surface deformation on the top surface of a metal plate, measured by using the method of laser vibrometry. The PINN is physically informed by the acoustic wave equation and its convergence is sped up using adaptive activation functions. The adaptive activation function uses a scalable hyperparameter in the activation function, which is optimized to achieve best performance of the network as it changes dynamically the topology of the loss function involved in the optimization process. The usage of adaptive activation function significantly improves the convergence, notably observed in the current study. We use PINNs to estimate the speed of sound of the metal plate, which we do with an error of 1\%, and then, by allowing the speed of sound to be space dependent, we identify and characterize the crack as the positions where the speed of sound has decreased. Our study also shows the effect of sub-sampling of the data on the sensitivity of sound speed estimates. More broadly, the resulting model shows a promising deep neural network model for ill-posed inverse problems.

Zermelo's problem: Optimal point-to-point navigation in 2D turbulent flows using Reinforcement Learning

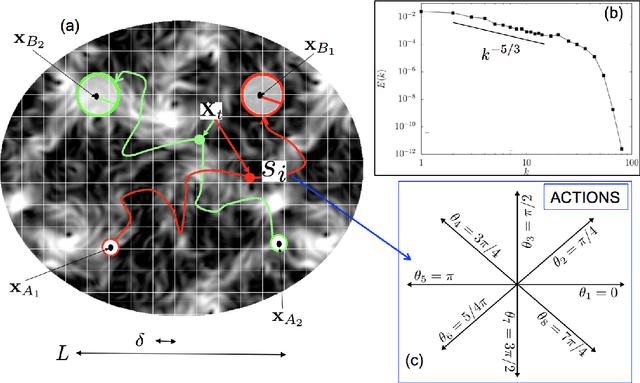
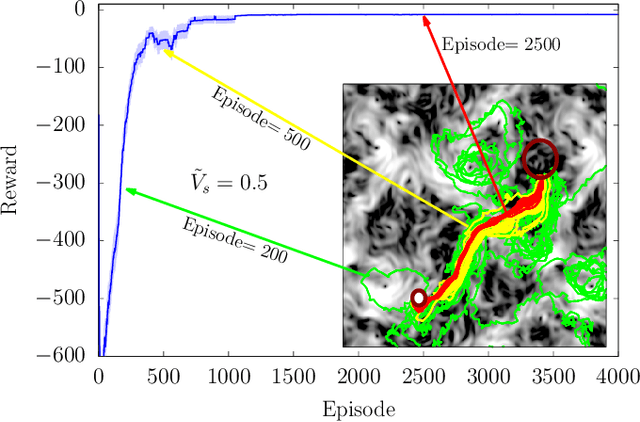
To find the path that minimizes the time to navigate between two given points in a fluid flow is known as the Zermelo's problem. Here, we investigate it by using a Reinforcement Learning (RL) approach for the case of a vessel which has a slip velocity with fixed intensity, V_s, but variable direction and navigating in a 2D turbulent sea. We use an Actor-Critic RL algorithm, and compare the results with strategies obtained analytically from continuous Optimal Navigation (ON) protocols. We show that for our application, ON solutions are unstable for the typical duration of the navigation process, and are therefore not useful in practice. On the other hand, RL solutions are much more robust with respect to small changes in the initial conditions and to external noise, and are able to find optimal trajectories even when V_s is much smaller than the maximum flow velocity. Furthermore, we show how the RL approach is able to take advantage of the flow properties in order to reach the target, especially when the steering speed is small.