Baseline Results for Selected Nonlinear System Identification Benchmarks

Nonlinear system identification remains an important open challenge across research and academia. Large numbers of novel approaches are seen published each year, each presenting improvements or extensions to existing methods. It is natural, therefore, to consider how one might choose between these competing models. Benchmark datasets provide one clear way to approach this question. However, to make meaningful inference based on benchmark performance it is important to understand how well a new method performs comparatively to results available with well-established methods. This paper presents a set of ten baseline techniques and their relative performances on five popular benchmarks. The aim of this contribution is to stimulate thought and discussion regarding objective comparison of identification methodologies.

Koopman Data-Driven Predictive Control with Robust Stability and Recursive Feasibility Guarantees

In this paper, we consider the design of data-driven predictive controllers for nonlinear systems from input-output data via linear-in-control input Koopman lifted models. Instead of identifying and simulating a Koopman model to predict future outputs, we design a subspace predictive controller in the Koopman space. This allows us to learn the observables minimizing the multi-step output prediction error of the Koopman subspace predictor, preventing the propagation of prediction errors. To avoid losing feasibility of our predictive control scheme due to prediction errors, we compute a terminal cost and terminal set in the Koopman space and we obtain recursive feasibility guarantees through an interpolated initial state. As a third contribution, we introduce a novel regularization cost yielding input-to-state stability guarantees with respect to the prediction error for the resulting closed-loop system. The performance of the developed Koopman data-driven predictive control methodology is illustrated on a nonlinear benchmark example from the literature.

State Derivative Normalization for Continuous-Time Deep Neural Networks

The importance of proper data normalization for deep neural networks is well known. However, in continuous-time state-space model estimation, it has been observed that improper normalization of either the hidden state or hidden state derivative of the model estimate, or even of the time interval can lead to numerical and optimization challenges with deep learning based methods. This results in a reduced model quality. In this contribution, we show that these three normalization tasks are inherently coupled. Due to the existence of this coupling, we propose a solution to all three normalization challenges by introducing a normalization constant at the state derivative level. We show that the appropriate choice of the normalization constant is related to the dynamics of the to-be-identified system and we derive multiple methods of obtaining an effective normalization constant. We compare and discuss all the normalization strategies on a benchmark problem based on experimental data from a cascaded tanks system and compare our results with other methods of the identification literature.

Physics-Informed Learning Using Hamiltonian Neural Networks with Output Error Noise Models

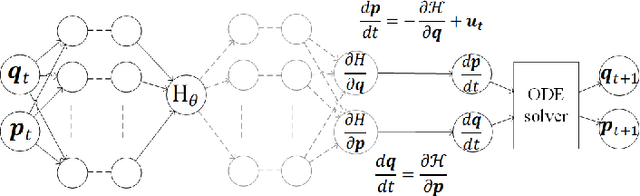
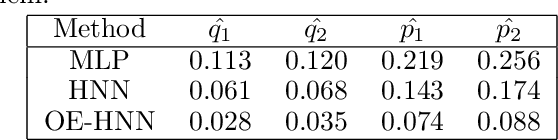
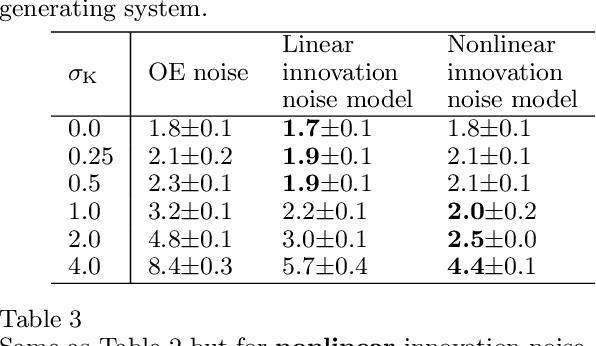
In order to make data-driven models of physical systems interpretable and reliable, it is essential to include prior physical knowledge in the modeling framework. Hamiltonian Neural Networks (HNNs) implement Hamiltonian theory in deep learning and form a comprehensive framework for modeling autonomous energy-conservative systems. Despite being suitable to estimate a wide range of physical system behavior from data, classical HNNs are restricted to systems without inputs and require noiseless state measurements and information on the derivative of the state to be available. To address these challenges, this paper introduces an Output Error Hamiltonian Neural Network (OE-HNN) modeling approach to address the modeling of physical systems with inputs and noisy state measurements. Furthermore, it does not require the state derivatives to be known. Instead, the OE-HNN utilizes an ODE-solver embedded in the training process, which enables the OE-HNN to learn the dynamics from noisy state measurements. In addition, extending HNNs based on the generalized Hamiltonian theory enables to include external inputs into the framework which are important for engineering applications. We demonstrate via simulation examples that the proposed OE-HNNs results in superior modeling performance compared to classical HNNs.

Initialization Approach for Nonlinear State-Space Identification via the Subspace Encoder Approach

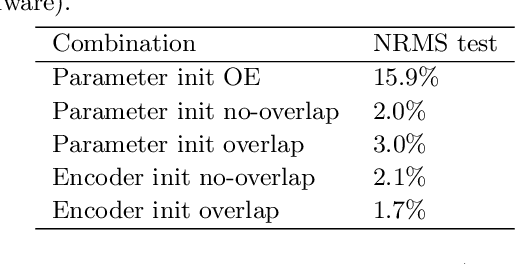
The SUBNET neural network architecture has been developed to identify nonlinear state-space models from input-output data. To achieve this, it combines the rolled-out nonlinear state-space equations and a state encoder function, both parameterised as neural networks The encoder function is introduced to reconstruct the current state from past input-output data. Hence, it enables the forward simulation of the rolled-out state-space model. While this approach has shown to provide high-accuracy and consistent model estimation, its convergence can be significantly improved by efficient initialization of the training process. This paper focuses on such an initialisation of the subspace encoder approach using the Best Linear Approximation (BLA). Using the BLA provided state-space matrices and its associated reconstructability map, both the state-transition part of the network and the encoder are initialized. The performance of the improved initialisation scheme is evaluated on a Wiener-Hammerstein simulation example and a benchmark dataset. The results show that for a weakly nonlinear system, the proposed initialisation based on the linear reconstructability map results in a faster convergence and a better model quality.

A Data-driven Pricing Scheme for Optimal Routing through Artificial Currencies

Mobility systems often suffer from a high price of anarchy due to the uncontrolled behavior of selfish users. This may result in societal costs that are significantly higher compared to what could be achieved by a centralized system-optimal controller. Monetary tolling schemes can effectively align the behavior of selfish users with the system-optimum. Yet, they inevitably discriminate the population in terms of income. Artificial currencies were recently presented as an effective alternative that can achieve the same performance, whilst guaranteeing fairness among the population. However, those studies were based on behavioral models that may differ from practical implementations. This paper presents a data-driven approach to automatically adapt artificial-currency tolls within repetitive-game settings. We first consider a parallel-arc setting whereby users commute on a daily basis from a unique origin to a unique destination, choosing a route in exchange of an artificial-currency price or reward while accounting for the impact of the choices of the other users on travel discomfort. Second, we devise a model-based reinforcement learning controller that autonomously learns the optimal pricing policy by interacting with the proposed framework considering the closeness of the observed aggregate flows to a desired system-optimal distribution as a reward function. Our numerical results show that the proposed data-driven pricing scheme can effectively align the users' flows with the system optimum, significantly reducing the societal costs with respect to the uncontrolled flows (by about 15% and 25% depending on the scenario), and respond to environmental changes in a robust and efficient manner.

Deep Subspace Encoders for Nonlinear System Identification

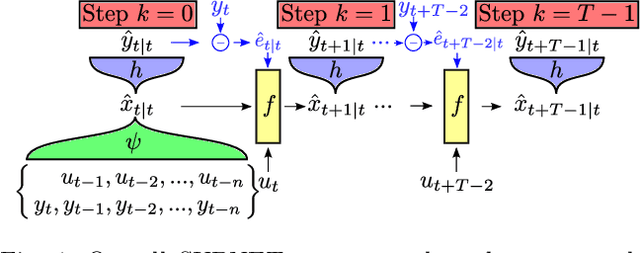
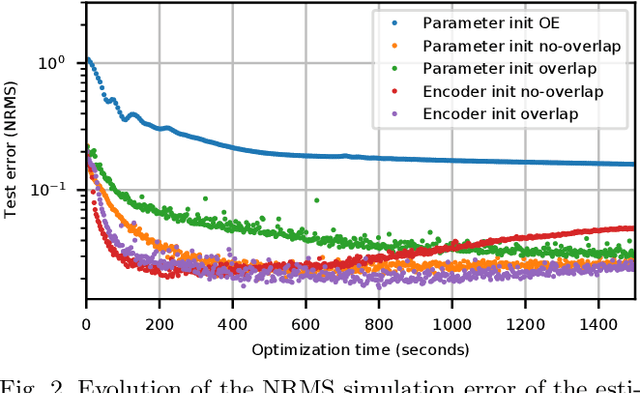
Using Artificial Neural Networks (ANN) for nonlinear system identification has proven to be a promising approach, but despite of all recent research efforts, many practical and theoretical problems still remain open. Specifically, noise handling and models, issues of consistency and reliable estimation under minimisation of the prediction error are the most severe problems. The latter comes with numerous practical challenges such as explosion of the computational cost in terms of the number of data samples and the occurrence of instabilities during optimization. In this paper, we aim to overcome these issues by proposing a method which uses a truncated prediction loss and a subspace encoder for state estimation. The truncated prediction loss is computed by selecting multiple truncated subsections from the time series and computing the average prediction loss. To obtain a computationally efficient estimation method that minimizes the truncated prediction loss, a subspace encoder represented by an artificial neural network is introduced. This encoder aims to approximate the state reconstructability map of the estimated model to provide an initial state for each truncated subsection given past inputs and outputs. By theoretical analysis, we show that, under mild conditions, the proposed method is locally consistent, increases optimization stability, and achieves increased data efficiency by allowing for overlap between the subsections. Lastly, we provide practical insights and user guidelines employing a numerical example and state-of-the-art benchmark results.

Deep subspace encoders for continuous-time state-space identification

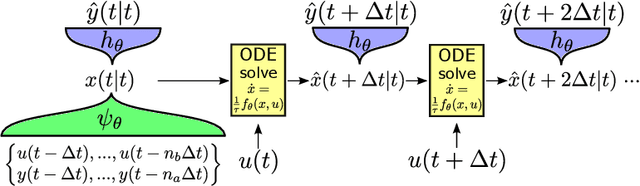
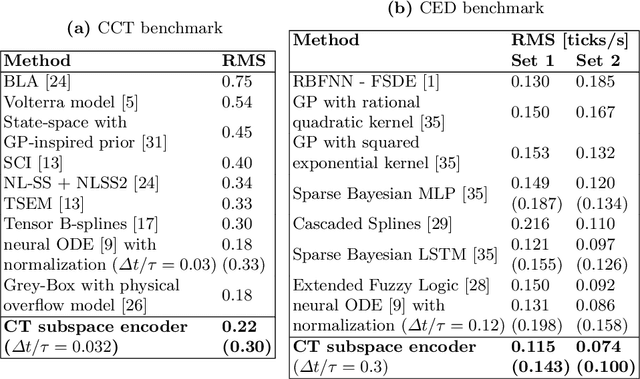
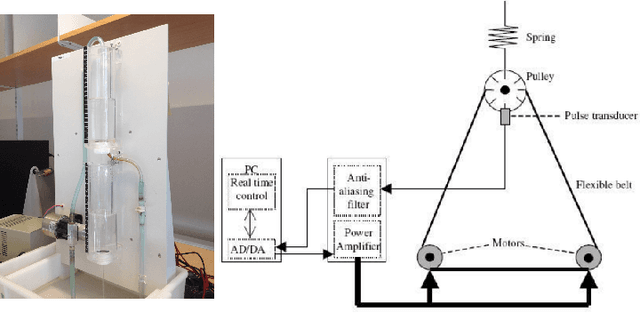
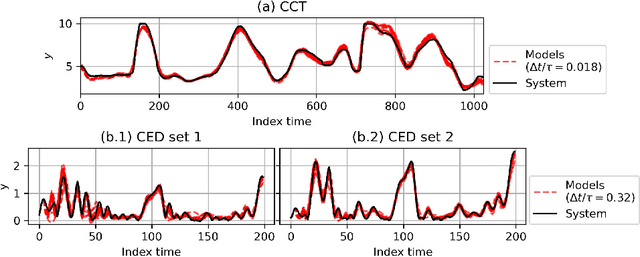
Continuous-time (CT) models have shown an improved sample efficiency during learning and enable ODE analysis methods for enhanced interpretability compared to discrete-time (DT) models. Even with numerous recent developments, the multifaceted CT state-space model identification problem remains to be solved in full, considering common experimental aspects such as the presence of external inputs, measurement noise, and latent states. This paper presents a novel estimation method that includes these aspects and that is able to obtain state-of-the-art results on multiple benchmarks where a small fully connected neural network describes the CT dynamics. The novel estimation method called the subspace encoder approach ascertains these results by altering the well-known simulation loss to include short subsections instead, by using an encoder function and a state-derivative normalization term to obtain a computationally feasible and stable optimization problem. This encoder function estimates the initial states of each considered subsection. We prove that the existence of the encoder function has the necessary condition of a Lipschitz continuous state-derivative utilizing established properties of ODEs.

Variational message passing for online polynomial NARMAX identification

We propose a variational Bayesian inference procedure for online nonlinear system identification. For each output observation, a set of parameter posterior distributions is updated, which is then used to form a posterior predictive distribution for future outputs. We focus on the class of polynomial NARMAX models, which we cast into probabilistic form and represent in terms of a Forney-style factor graph. Inference in this graph is efficiently performed by a variational message passing algorithm. We show empirically that our variational Bayesian estimator outperforms an online recursive least-squares estimator, most notably in small sample size settings and low noise regimes, and performs on par with an iterative least-squares estimator trained offline.

Deep Identification of Nonlinear Systems in Koopman Form

The present paper treats the identification of nonlinear dynamical systems using Koopman-based deep state-space encoders. Through this method, the usual drawback of needing to choose a dictionary of lifting functions a priori is circumvented. The encoder represents the lifting function to the space where the dynamics are linearly propagated using the Koopman operator. An input-affine formulation is considered for the lifted model structure and we address both full and partial state availability. The approach is implemented using the the deepSI toolbox in Python. To lower the computational need of the simulation error-based training, the data is split into subsections where multi-step prediction errors are calculated independently. This formulation allows for efficient batch optimization of the network parameters and, at the same time, excellent long term prediction capabilities of the obtained models. The performance of the approach is illustrated by nonlinear benchmark examples.