Koopman operator theory: fundamentals, control, and applications

The Koopman operator has gained considerable attention due to its ability to provide a global linear representation of highly complex dynamical systems. The operator describes nonlinear dynamics in a linear way through the lens of real- or complex-valued observable functions. Recently proposed data-driven techniques, like extended dynamic mode decomposition (EDMD), its kernelized variant, and machine-learning methods, can be used to generate finite-dimensional approximations accompanied by finite-data error bounds. In this tutorial paper, we provide a concise introduction into Koopman operator theory and its use in systems and control. A particular focus is put on data-driven surrogate models, their extension to systems with inputs, and controller design using Koopman operator theory. Moreover, we demonstrate the key techniques, i.e., EDMD and Koopman MPC. To this end, we provide simulation studies including source code on GitHub to enable the interested reader to experience the Koopman operator in systems and control step by step.

Autonomous Driving with Priority-Ordered STL Specifications Under Multimodal Uncertainty

Autonomous vehicles must plan trajectories that satisfy a multitude of requirements on safety, passenger comfort, and compliance with traffic rules. However, in safety-critical scenarios, it is not always possible to satisfy all requirements simultaneously, necessitating their prioritization based on importance. At the same time, in these safety-critical scenarios, the uncertainty in trajectory predictions of the surrounding traffic, such as other vehicles and pedestrians, should be explicitly accounted for. In this work, we propose an uncertainty-aware trajectory planning framework that incorporates a predefined lexicographic ordering over Signal Temporal Logic (STL) specifications that stays valid under uncertainty. We implement this formulation with Model Predictive Path Integral (MPPI) control and we demonstrate the effectiveness of our method on simulation scenarios, showing that our framework efficiently handles conflicting objectives under realistic multi-modal uncertainty.

PE-MHL: Physics-Encoded Modular Hybrid Layers for Scalable Learning of Complex Systems

Hybrid models that combine physics-based and data-driven components have shown strong potential for achieving accuracy and interpretability in control applications. While recent methods have made progress in incorporating physical consistency, challenges remain in scalability, robustness to noise, and control of model complexity. This paper proposes a Physics-Encoded Modular Hybrid Layer (PE-MHL) framework, in which a baseline physics-based model is incrementally refined through the addition of new sub-models, where each new component adds complexity while preserving what previous components have already learned. We establish a theoretical guarantee for this construction: with a least-squares initialization of each new sub-model, the training error is monotonically non-increasing in the number of sub-models and provably converges. Empirical evaluations on a nonlinear NARX benchmark and the Quanser Aero 2 platform demonstrate that PE-MHL outperforms equivalently sized monolithic networks in both accuracy and generalization, while also providing more stable training dynamics and better preservation of underlying data structures.

A Unified Representation of Neural Networks Architectures

In this paper we consider the limiting case of neural networks (NNs) architectures when the number of neurons in each hidden layer and the number of hidden layers tend to infinity thus forming a continuum, and we derive approximation errors as a function of the number of neurons and/or hidden layers. Firstly, we consider the case of neural networks with a single hidden layer and we derive an integral infinite width neural representation that generalizes existing continuous neural networks (CNNs) representations. Then we extend this to deep residual CNNs that have a finite number of integral hidden layers and residual connections. Secondly, we revisit the relation between neural ODEs and deep residual NNs and we formalize approximation errors via discretization techniques. Then, we merge these two approaches into a unified homogeneous representation of NNs as a Distributed Parameter neural Network (DiPaNet) and we show that most of the existing finite and infinite-dimensional NNs architectures are related via homogenization/discretization with the DiPaNet representation. Our approach is purely deterministic and applies to general, uniformly continuous matrix weight functions. Relations with neural fields and other neural integro-differential equations are discussed along with further possible generalizations and applications of the DiPaNet framework.

From Product Hilbert Spaces to the Generalized Koopman Operator and the Nonlinear Fundamental Lemma

The generalization of the Koopman operator to systems with control input and the derivation of a nonlinear fundamental lemma are two open problems that play a key role in the development of data-driven control methods for nonlinear systems. Both problems hinge on the construction of observable or basis functions and their corresponding Hilbert space that enable an infinite-dimensional, linear system representation. In this paper we derive a novel solution to these problems based on orthonormal expansion in a product Hilbert space constructed as the tensor product between the Hilbert spaces of the state and input observable functions, respectively. We prove that there exists an infinite-dimensional linear operator, i.e. the generalized Koopman operator, from the constructed product Hilbert space to the Hilbert space corresponding to the lifted state propagated forward in time. A scalable data-driven method for computing finite-dimensional approximations of generalized Koopman operators and several choices of observable functions are also presented. Moreover, we derive a nonlinear fundamental lemma by exploiting the bilinear structure of the infinite-dimensional generalized Koopman model. The effectiveness of the developed generalized Koopman embedding is illustrated on the Van der Pol oscillator.

Deep Operator Neural Network Model Predictive Control

In this paper, we consider the design of model predictive control (MPC) algorithms based on deep operator neural networks (DeepONets). These neural networks are capable of accurately approximating real and complex valued solutions of continuous time nonlinear systems without relying on recurrent architectures. The DeepONet architecture is made up of two feedforward neural networks: the branch network, which encodes the input function space, and the trunk network, which represents dependencies on temporal variables or initial conditions. Utilizing the original DeepONet architecture as a predictor within MPC for Multi Input Multi Output (MIMO) systems requires multiple branch networks, to generate multi output predictions, one for each input. Moreover, to predict multiple time steps into the future, the network has to be evaluated multiple times. Motivated by this, we introduce a multi step DeepONet (MS-DeepONet) architecture that computes in one shot multi step predictions of system outputs from multi step input sequences, which is better suited for MPC. We prove that the MS DeepONet is a universal approximator in terms of multi step sequence prediction. Additionally, we develop automated hyper parameter selection strategies and implement MPC frameworks using both the standard DeepONet and the proposed MS DeepONet architectures in PyTorch. The implementation is publicly available on GitHub. Simulation results demonstrate that MS-DeepONet consistently outperforms the standard DeepONet in learning and predictive control tasks across several nonlinear benchmark systems: the van der Pol oscillator, the quadruple tank process, and a cart pendulum unstable system, where it successfully learns and executes multiple swing up and stabilization policies.

Koopman Data-Driven Predictive Control with Robust Stability and Recursive Feasibility Guarantees

In this paper, we consider the design of data-driven predictive controllers for nonlinear systems from input-output data via linear-in-control input Koopman lifted models. Instead of identifying and simulating a Koopman model to predict future outputs, we design a subspace predictive controller in the Koopman space. This allows us to learn the observables minimizing the multi-step output prediction error of the Koopman subspace predictor, preventing the propagation of prediction errors. To avoid losing feasibility of our predictive control scheme due to prediction errors, we compute a terminal cost and terminal set in the Koopman space and we obtain recursive feasibility guarantees through an interpolated initial state. As a third contribution, we introduce a novel regularization cost yielding input-to-state stability guarantees with respect to the prediction error for the resulting closed-loop system. The performance of the developed Koopman data-driven predictive control methodology is illustrated on a nonlinear benchmark example from the literature.

Basis functions nonlinear data-enabled predictive control: Consistent and computationally efficient formulations

This paper considers the extension of data-enabled predictive control (DeePC) to nonlinear systems via general basis functions. Firstly, we formulate a basis functions DeePC behavioral predictor and we identify necessary and sufficient conditions for equivalence with a corresponding basis functions multi-step identified predictor. The derived conditions yield a dynamic regularization cost function that enables a well-posed (i.e., consistent) basis functions formulation of nonlinear DeePC. To optimize computational efficiency of basis functions DeePC we further develop two alternative formulations that use a simpler, sparse regularization cost function and ridge regression, respectively. Consistency implications for Koopman DeePC as well as several methods for constructing the basis functions representation are also indicated. The effectiveness of the developed consistent basis functions DeePC formulations is illustrated on a benchmark nonlinear pendulum state-space model, for both noise free and noisy data.

On feedforward control using physics-guided neural networks: Training cost regularization and optimized initialization

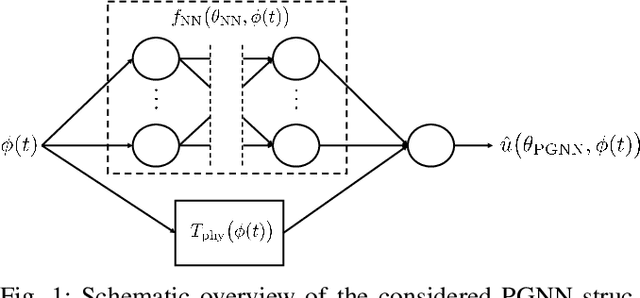
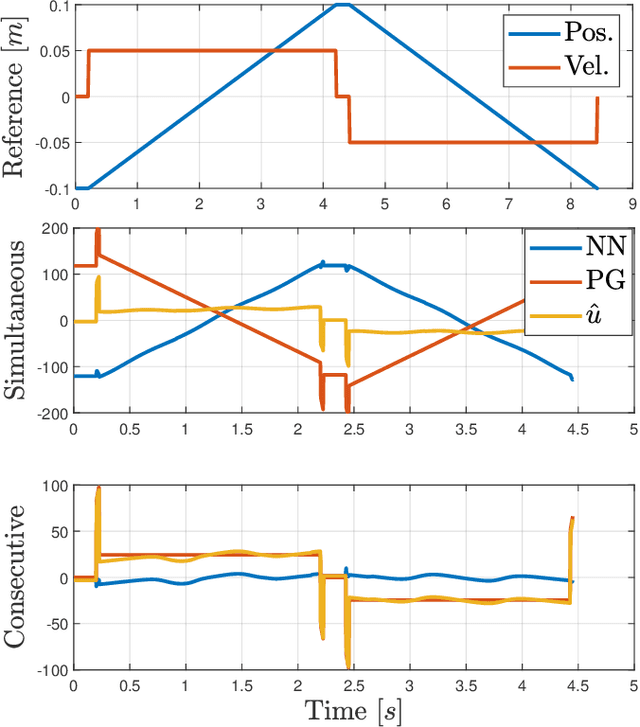
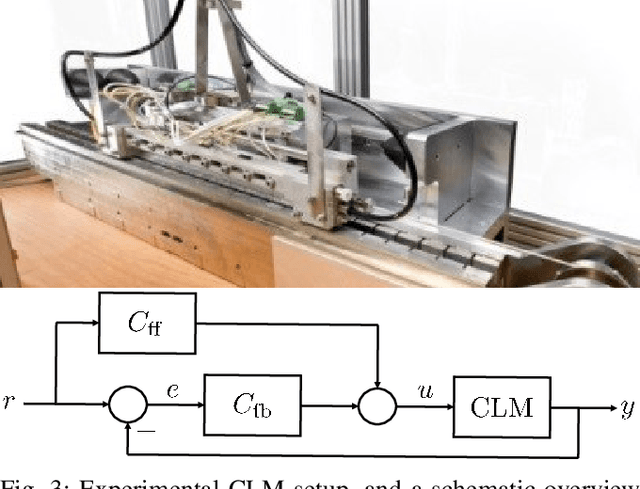
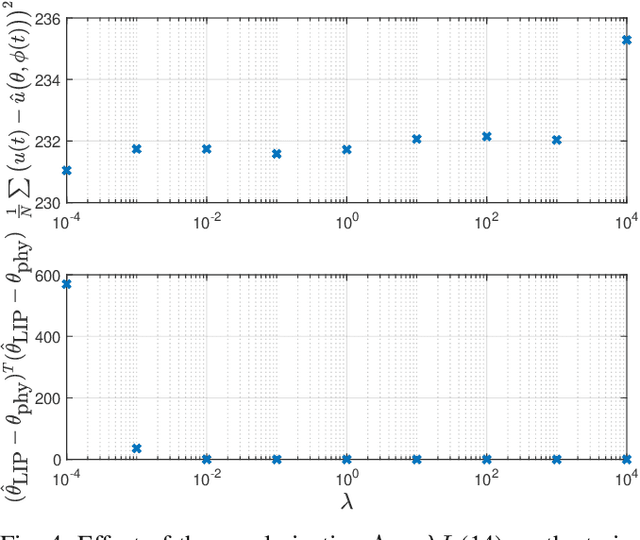
Performance of model-based feedforward controllers is typically limited by the accuracy of the inverse system dynamics model. Physics-guided neural networks (PGNN), where a known physical model cooperates in parallel with a neural network, were recently proposed as a method to achieve high accuracy of the identified inverse dynamics. However, the flexible nature of neural networks can create overparameterization when employed in parallel with a physical model, which results in a parameter drift during training. This drift may result in parameters of the physical model not corresponding to their physical values, which increases vulnerability of the PGNN to operating conditions not present in the training data. To address this problem, this paper proposes a regularization method via identified physical parameters, in combination with an optimized training initialization that improves training convergence. The regularized PGNN framework is validated on a real-life industrial linear motor, where it delivers better tracking accuracy and extrapolation.