CoCoAFusE: Beyond Mixtures of Experts via Model Fusion

Many learning problems involve multiple patterns and varying degrees of uncertainty dependent on the covariates. Advances in Deep Learning (DL) have addressed these issues by learning highly nonlinear input-output dependencies. However, model interpretability and Uncertainty Quantification (UQ) have often straggled behind. In this context, we introduce the Competitive/Collaborative Fusion of Experts (CoCoAFusE), a novel, Bayesian Covariates-Dependent Modeling technique. CoCoAFusE builds on the very philosophy behind Mixtures of Experts (MoEs), blending predictions from several simple sub-models (or "experts") to achieve high levels of expressiveness while retaining a substantial degree of local interpretability. Our formulation extends that of a classical Mixture of Experts by contemplating the fusion of the experts' distributions in addition to their more usual mixing (i.e., superimposition). Through this additional feature, CoCoAFusE better accommodates different scenarios for the intermediate behavior between generating mechanisms, resulting in tighter credible bounds on the response variable. Indeed, only resorting to mixing, as in classical MoEs, may lead to multimodality artifacts, especially over smooth transitions. Instead, CoCoAFusE can avoid these artifacts even under the same structure and priors for the experts, leading to greater expressiveness and flexibility in modeling. This new approach is showcased extensively on a suite of motivating numerical examples and a collection of real-data ones, demonstrating its efficacy in tackling complex regression problems where uncertainty is a key quantity of interest.

In-Context Learning for Zero-Shot Speed Estimation of BLDC motors

Accurate speed estimation in sensorless brushless DC motors is essential for high-performance control and monitoring, yet conventional model-based approaches struggle with system nonlinearities and parameter uncertainties. In this work, we propose an in-context learning framework leveraging transformer-based models to perform zero-shot speed estimation using only electrical measurements. By training the filter offline on simulated motor trajectories, we enable real-time inference on unseen real motors without retraining, eliminating the need for explicit system identification while retaining adaptability to varying operating conditions. Experimental results demonstrate that our method outperforms traditional Kalman filter-based estimators, especially in low-speed regimes that are crucial during motor startup.

Koopman Data-Driven Predictive Control with Robust Stability and Recursive Feasibility Guarantees

In this paper, we consider the design of data-driven predictive controllers for nonlinear systems from input-output data via linear-in-control input Koopman lifted models. Instead of identifying and simulating a Koopman model to predict future outputs, we design a subspace predictive controller in the Koopman space. This allows us to learn the observables minimizing the multi-step output prediction error of the Koopman subspace predictor, preventing the propagation of prediction errors. To avoid losing feasibility of our predictive control scheme due to prediction errors, we compute a terminal cost and terminal set in the Koopman space and we obtain recursive feasibility guarantees through an interpolated initial state. As a third contribution, we introduce a novel regularization cost yielding input-to-state stability guarantees with respect to the prediction error for the resulting closed-loop system. The performance of the developed Koopman data-driven predictive control methodology is illustrated on a nonlinear benchmark example from the literature.

SINDy vs Hard Nonlinearities and Hidden Dynamics: a Benchmarking Study

In this work we analyze the effectiveness of the Sparse Identification of Nonlinear Dynamics (SINDy) technique on three benchmark datasets for nonlinear identification, to provide a better understanding of its suitability when tackling real dynamical systems. While SINDy can be an appealing strategy for pursuing physics-based learning, our analysis highlights difficulties in dealing with unobserved states and non-smooth dynamics. Due to the ubiquity of these features in real systems in general, and control applications in particular, we complement our analysis with hands-on approaches to tackle these issues in order to exploit SINDy also in these challenging contexts.

Explainable data-driven modeling via mixture of experts: towards effective blending of grey and black-box models

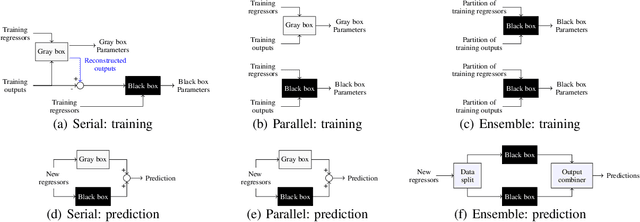
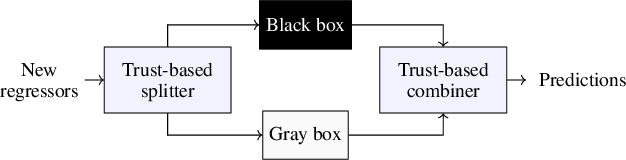
Traditional models grounded in first principles often struggle with accuracy as the system's complexity increases. Conversely, machine learning approaches, while powerful, face challenges in interpretability and in handling physical constraints. Efforts to combine these models often often stumble upon difficulties in finding a balance between accuracy and complexity. To address these issues, we propose a comprehensive framework based on a "mixture of experts" rationale. This approach enables the data-based fusion of diverse local models, leveraging the full potential of first-principle-based priors. Our solution allows independent training of experts, drawing on techniques from both machine learning and system identification, and it supports both collaborative and competitive learning paradigms. To enhance interpretability, we penalize abrupt variations in the expert's combination. Experimental results validate the effectiveness of our approach in producing an interpretable combination of models closely resembling the target phenomena.

META-SMGO-$Δ$: similarity as a prior in black-box optimization

When solving global optimization problems in practice, one often ends up repeatedly solving problems that are similar to each others. By providing a rigorous definition of similarity, in this work we propose to incorporate the META-learning rationale into SMGO-$\Delta$, a global optimization approach recently proposed in the literature, to exploit priors obtained from similar past experience to efficiently solve new (similar) problems. Through a benchmark numerical example we show the practical benefits of our META-extension of the baseline algorithm, while providing theoretical bounds on its performance.