HypeRL: Parameter-Informed Reinforcement Learning for Parametric PDEs

In this work, we devise a new, general-purpose reinforcement learning strategy for the optimal control of parametric partial differential equations (PDEs). Such problems frequently arise in applied sciences and engineering and entail a significant complexity when control and/or state variables are distributed in high-dimensional space or depend on varying parameters. Traditional numerical methods, relying on either iterative minimization algorithms or dynamic programming, while reliable, often become computationally infeasible. Indeed, in either way, the optimal control problem must be solved for each instance of the parameters, and this is out of reach when dealing with high-dimensional time-dependent and parametric PDEs. In this paper, we propose HypeRL, a deep reinforcement learning (DRL) framework to overcome the limitations shown by traditional methods. HypeRL aims at approximating the optimal control policy directly. Specifically, we employ an actor-critic DRL approach to learn an optimal feedback control strategy that can generalize across the range of variation of the parameters. To effectively learn such optimal control laws, encoding the parameter information into the DRL policy and value function neural networks (NNs) is essential. To do so, HypeRL uses two additional NNs, often called hypernetworks, to learn the weights and biases of the value function and the policy NNs. We validate the proposed approach on two PDE-constrained optimal control benchmarks, namely a 1D Kuramoto-Sivashinsky equation and a 2D Navier-Stokes equations, by showing that the knowledge of the PDE parameters and how this information is encoded, i.e., via a hypernetwork, is an essential ingredient for learning parameter-dependent control policies that can generalize effectively to unseen scenarios and for improving the sample efficiency of such policies.

Latent feedback control of distributed systems in multiple scenarios through deep learning-based reduced order models

Continuous monitoring and real-time control of high-dimensional distributed systems are often crucial in applications to ensure a desired physical behavior, without degrading stability and system performances. Traditional feedback control design that relies on full-order models, such as high-dimensional state-space representations or partial differential equations, fails to meet these requirements due to the delay in the control computation, which requires multiple expensive simulations of the physical system. The computational bottleneck is even more severe when considering parametrized systems, as new strategies have to be determined for every new scenario. To address these challenges, we propose a real-time closed-loop control strategy enhanced by nonlinear non-intrusive Deep Learning-based Reduced Order Models (DL-ROMs). Specifically, in the offline phase, (i) full-order state-control pairs are generated for different scenarios through the adjoint method, (ii) the essential features relevant for control design are extracted from the snapshots through a combination of Proper Orthogonal Decomposition (POD) and deep autoencoders, and (iii) the low-dimensional policy bridging latent control and state spaces is approximated with a feedforward neural network. After data generation and neural networks training, the optimal control actions are retrieved in real-time for any observed state and scenario. In addition, the dynamics may be approximated through a cheap surrogate model in order to close the loop at the latent level, thus continuously controlling the system in real-time even when full-order state measurements are missing. The effectiveness of the proposed method, in terms of computational speed, accuracy, and robustness against noisy data, is finally assessed on two different high-dimensional optimal transport problems, one of which also involving an underlying fluid flow.

Handling geometrical variability in nonlinear reduced order modeling through Continuous Geometry-Aware DL-ROMs

Deep Learning-based Reduced Order Models (DL-ROMs) provide nowadays a well-established class of accurate surrogate models for complex physical systems described by parametrized PDEs, by nonlinearly compressing the solution manifold into a handful of latent coordinates. Until now, design and application of DL-ROMs mainly focused on physically parameterized problems. Within this work, we provide a novel extension of these architectures to problems featuring geometrical variability and parametrized domains, namely, we propose Continuous Geometry-Aware DL-ROMs (CGA-DL-ROMs). In particular, the space-continuous nature of the proposed architecture matches the need to deal with multi-resolution datasets, which are quite common in the case of geometrically parametrized problems. Moreover, CGA-DL-ROMs are endowed with a strong inductive bias that makes them aware of geometrical parametrizations, thus enhancing both the compression capability and the overall performance of the architecture. Within this work, we justify our findings through a thorough theoretical analysis, and we practically validate our claims by means of a series of numerical tests encompassing physically-and-geometrically parametrized PDEs, ranging from the unsteady Navier-Stokes equations for fluid dynamics to advection-diffusion-reaction equations for mathematical biology.

Interpretable and Efficient Data-driven Discovery and Control of Distributed Systems

Effectively controlling systems governed by Partial Differential Equations (PDEs) is crucial in several fields of Applied Sciences and Engineering. These systems usually yield significant challenges to conventional control schemes due to their nonlinear dynamics, partial observability, high-dimensionality once discretized, distributed nature, and the requirement for low-latency feedback control. Reinforcement Learning (RL), particularly Deep RL (DRL), has recently emerged as a promising control paradigm for such systems, demonstrating exceptional capabilities in managing high-dimensional, nonlinear dynamics. However, DRL faces challenges including sample inefficiency, robustness issues, and an overall lack of interpretability. To address these issues, we propose a data-efficient, interpretable, and scalable Dyna-style Model-Based RL framework for PDE control, combining the Sparse Identification of Nonlinear Dynamics with Control (SINDy-C) algorithm and an autoencoder (AE) framework for the sake of dimensionality reduction of PDE states and actions. This novel approach enables fast rollouts, reducing the need for extensive environment interactions, and provides an interpretable latent space representation of the PDE forward dynamics. We validate our method on two PDE problems describing fluid flows - namely, the 1D Burgers equation and 2D Navier-Stokes equations - comparing it against a model-free baseline, and carrying out an extensive analysis of the learned dynamics.

Real-time optimal control of high-dimensional parametrized systems by deep learning-based reduced order models

Steering a system towards a desired target in a very short amount of time is challenging from a computational standpoint. Indeed, the intrinsically iterative nature of optimal control problems requires multiple simulations of the physical system to be controlled. Moreover, the control action needs to be updated whenever the underlying scenario undergoes variations. Full-order models based on, e.g., the Finite Element Method, do not meet these requirements due to the computational burden they usually entail. On the other hand, conventional reduced order modeling techniques such as the Reduced Basis method, are intrusive, rely on a linear superimposition of modes, and lack of efficiency when addressing nonlinear time-dependent dynamics. In this work, we propose a non-intrusive Deep Learning-based Reduced Order Modeling (DL-ROM) technique for the rapid control of systems described in terms of parametrized PDEs in multiple scenarios. In particular, optimal full-order snapshots are generated and properly reduced by either Proper Orthogonal Decomposition or deep autoencoders (or a combination thereof) while feedforward neural networks are exploited to learn the map from scenario parameters to reduced optimal solutions. Nonlinear dimensionality reduction therefore allows us to consider state variables and control actions that are both low-dimensional and distributed. After (i) data generation, (ii) dimensionality reduction, and (iii) neural networks training in the offline phase, optimal control strategies can be rapidly retrieved in an online phase for any scenario of interest. The computational speedup and the high accuracy obtained with the proposed approach are assessed on different PDE-constrained optimization problems, ranging from the minimization of energy dissipation in incompressible flows modelled through Navier-Stokes equations to the thermal active cooling in heat transfer.

On latent dynamics learning in nonlinear reduced order modeling

In this work, we present the novel mathematical framework of latent dynamics models (LDMs) for reduced order modeling of parameterized nonlinear time-dependent PDEs. Our framework casts this latter task as a nonlinear dimensionality reduction problem, while constraining the latent state to evolve accordingly to an (unknown) dynamical system. A time-continuous setting is employed to derive error and stability estimates for the LDM approximation of the full order model (FOM) solution. We analyze the impact of using an explicit Runge-Kutta scheme in the time-discrete setting, resulting in the $\Delta\text{LDM}$ formulation, and further explore the learnable setting, $\Delta\text{LDM}_\theta$, where deep neural networks approximate the discrete LDM components, while providing a bounded approximation error with respect to the FOM. Moreover, we extend the concept of parameterized Neural ODE - recently proposed as a possible way to build data-driven dynamical systems with varying input parameters - to be a convolutional architecture, where the input parameters information is injected by means of an affine modulation mechanism, while designing a convolutional autoencoder neural network able to retain spatial-coherence, thus enhancing interpretability at the latent level. Numerical experiments, including the Burgers' and the advection-reaction-diffusion equations, demonstrate the framework's ability to obtain, in a multi-query context, a time-continuous approximation of the FOM solution, thus being able to query the LDM approximation at any given time instance while retaining a prescribed level of accuracy. Our findings highlight the remarkable potential of the proposed LDMs, representing a mathematically rigorous framework to enhance the accuracy and approximation capabilities of reduced order modeling for time-dependent parameterized PDEs.

VENI, VINDy, VICI: a variational reduced-order modeling framework with uncertainty quantification

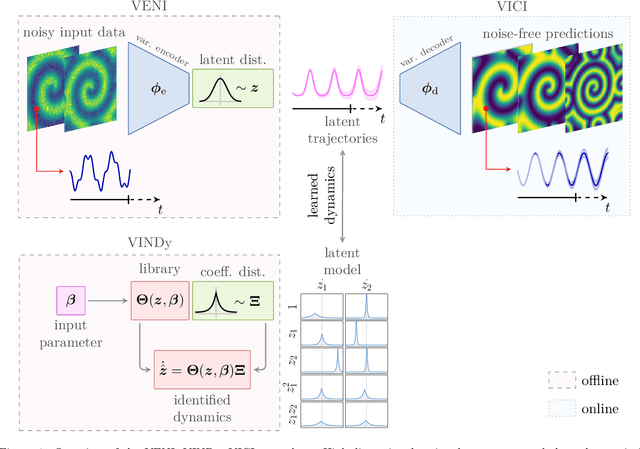
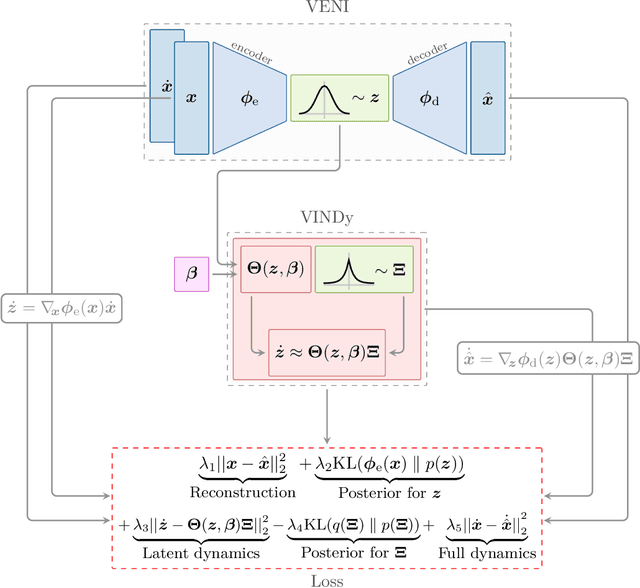
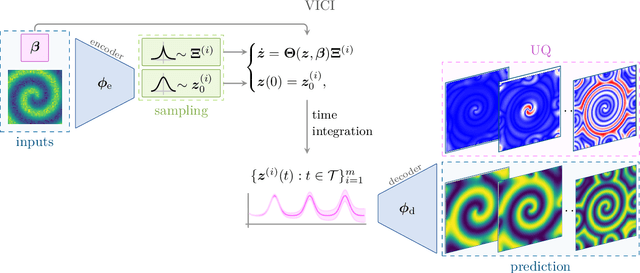
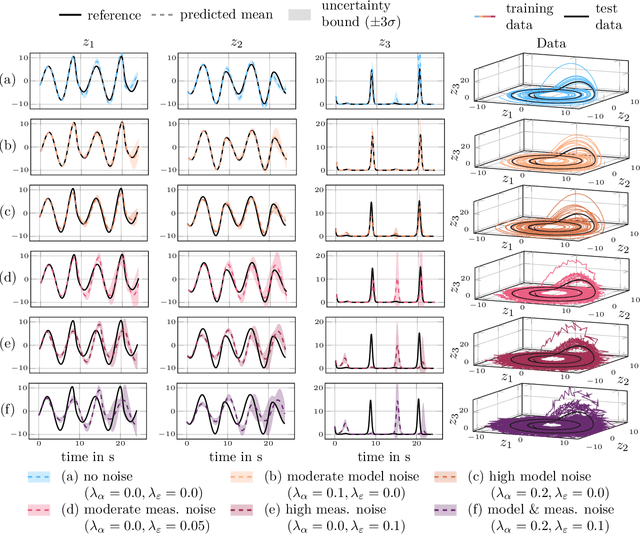
The simulation of many complex phenomena in engineering and science requires solving expensive, high-dimensional systems of partial differential equations (PDEs). To circumvent this, reduced-order models (ROMs) have been developed to speed up computations. However, when governing equations are unknown or partially known, typically ROMs lack interpretability and reliability of the predicted solutions. In this work we present a data-driven, non-intrusive framework for building ROMs where the latent variables and dynamics are identified in an interpretable manner and uncertainty is quantified. Starting from a limited amount of high-dimensional, noisy data the proposed framework constructs an efficient ROM by leveraging variational autoencoders for dimensionality reduction along with a newly introduced, variational version of sparse identification of nonlinear dynamics (SINDy), which we refer to as Variational Identification of Nonlinear Dynamics (VINDy). In detail, the method consists of Variational Encoding of Noisy Inputs (VENI) to identify the distribution of reduced coordinates. Simultaneously, we learn the distribution of the coefficients of a pre-determined set of candidate functions by VINDy. Once trained offline, the identified model can be queried for new parameter instances and new initial conditions to compute the corresponding full-time solutions. The probabilistic setup enables uncertainty quantification as the online testing consists of Variational Inference naturally providing Certainty Intervals (VICI). In this work we showcase the effectiveness of the newly proposed VINDy method in identifying interpretable and accurate dynamical system for the R\"ossler system with different noise intensities and sources. Then the performance of the overall method - named VENI, VINDy, VICI - is tested on PDE benchmarks including structural mechanics and fluid dynamics.

Recurrent Deep Kernel Learning of Dynamical Systems

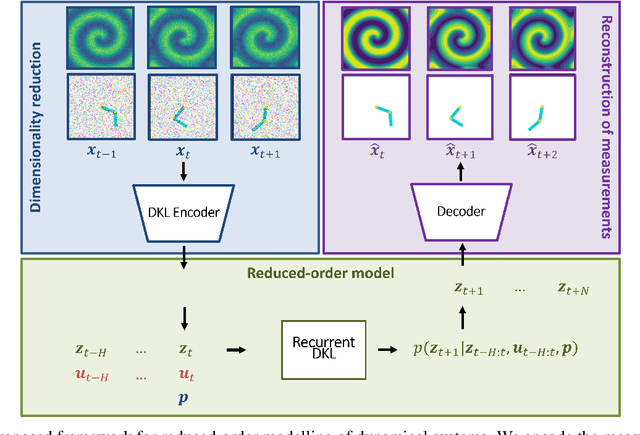
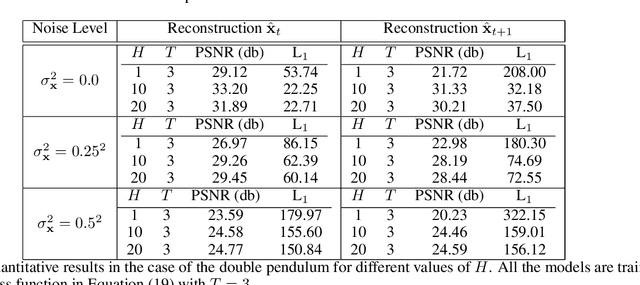
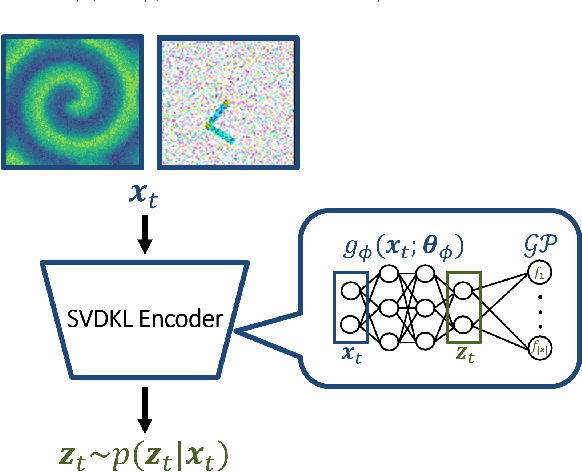
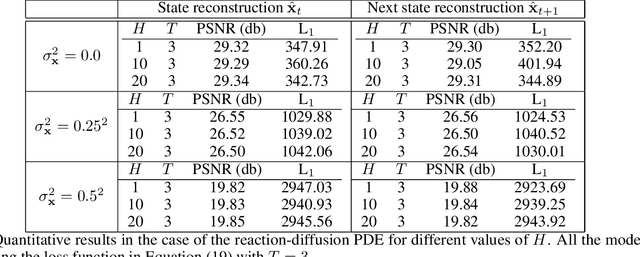
Digital twins require computationally-efficient reduced-order models (ROMs) that can accurately describe complex dynamics of physical assets. However, constructing ROMs from noisy high-dimensional data is challenging. In this work, we propose a data-driven, non-intrusive method that utilizes stochastic variational deep kernel learning (SVDKL) to discover low-dimensional latent spaces from data and a recurrent version of SVDKL for representing and predicting the evolution of latent dynamics. The proposed method is demonstrated with two challenging examples -- a double pendulum and a reaction-diffusion system. Results show that our framework is capable of (i) denoising and reconstructing measurements, (ii) learning compact representations of system states, (iii) predicting system evolution in low-dimensional latent spaces, and (iv) quantifying modeling uncertainties.

PTPI-DL-ROMs: pre-trained physics-informed deep learning-based reduced order models for nonlinear parametrized PDEs

The coupling of Proper Orthogonal Decomposition (POD) and deep learning-based ROMs (DL-ROMs) has proved to be a successful strategy to construct non-intrusive, highly accurate, surrogates for the real time solution of parametric nonlinear time-dependent PDEs. Inexpensive to evaluate, POD-DL-ROMs are also relatively fast to train, thanks to their limited complexity. However, POD-DL-ROMs account for the physical laws governing the problem at hand only through the training data, that are usually obtained through a full order model (FOM) relying on a high-fidelity discretization of the underlying equations. Moreover, the accuracy of POD-DL-ROMs strongly depends on the amount of available data. In this paper, we consider a major extension of POD-DL-ROMs by enforcing the fulfillment of the governing physical laws in the training process -- that is, by making them physics-informed -- to compensate for possible scarce and/or unavailable data and improve the overall reliability. To do that, we first complement POD-DL-ROMs with a trunk net architecture, endowing them with the ability to compute the problem's solution at every point in the spatial domain, and ultimately enabling a seamless computation of the physics-based loss by means of the strong continuous formulation. Then, we introduce an efficient training strategy that limits the notorious computational burden entailed by a physics-informed training phase. In particular, we take advantage of the few available data to develop a low-cost pre-training procedure; then, we fine-tune the architecture in order to further improve the prediction reliability. Accuracy and efficiency of the resulting pre-trained physics-informed DL-ROMs (PTPI-DL-ROMs) are then assessed on a set of test cases ranging from non-affinely parametrized advection-diffusion-reaction equations, to nonlinear problems like the Navier-Stokes equations for fluid flows.

SINDy vs Hard Nonlinearities and Hidden Dynamics: a Benchmarking Study

In this work we analyze the effectiveness of the Sparse Identification of Nonlinear Dynamics (SINDy) technique on three benchmark datasets for nonlinear identification, to provide a better understanding of its suitability when tackling real dynamical systems. While SINDy can be an appealing strategy for pursuing physics-based learning, our analysis highlights difficulties in dealing with unobserved states and non-smooth dynamics. Due to the ubiquity of these features in real systems in general, and control applications in particular, we complement our analysis with hands-on approaches to tackle these issues in order to exploit SINDy also in these challenging contexts.