Data-driven identification of latent port-Hamiltonian systems

Conventional physics-based modeling techniques involve high effort, e.g., time and expert knowledge, while data-driven methods often lack interpretability, structure, and sometimes reliability. To mitigate this, we present a data-driven system identification framework that derives models in the port-Hamiltonian (pH) formulation. This formulation is suitable for multi-physical systems while guaranteeing the useful system theoretical properties of passivity and stability. Our framework combines linear and nonlinear reduction with structured, physics-motivated system identification. In this process, high-dimensional state data obtained from possibly nonlinear systems serves as input for an autoencoder, which then performs two tasks: (i) nonlinearly transforming and (ii) reducing this data onto a low-dimensional latent space. In this space, a linear pH system, that satisfies the pH properties per construction, is parameterized by the weights of a neural network. The mathematical requirements are met by defining the pH matrices through Cholesky factorizations. The neural networks that define the coordinate transformation and the pH system are identified in a joint optimization process to match the dynamics observed in the data while defining a linear pH system in the latent space. The learned, low-dimensional pH system can describe even nonlinear systems and is rapidly computable due to its small size. The method is exemplified by a parametric mass-spring-damper and a nonlinear pendulum example, as well as the high-dimensional model of a disc brake with linear thermoelastic behavior.

VENI, VINDy, VICI: a variational reduced-order modeling framework with uncertainty quantification

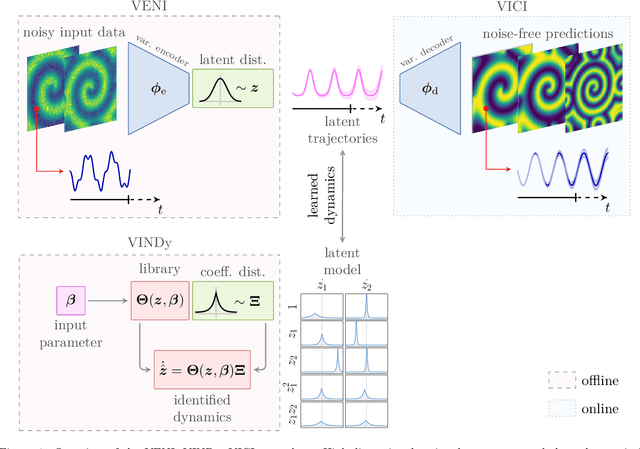
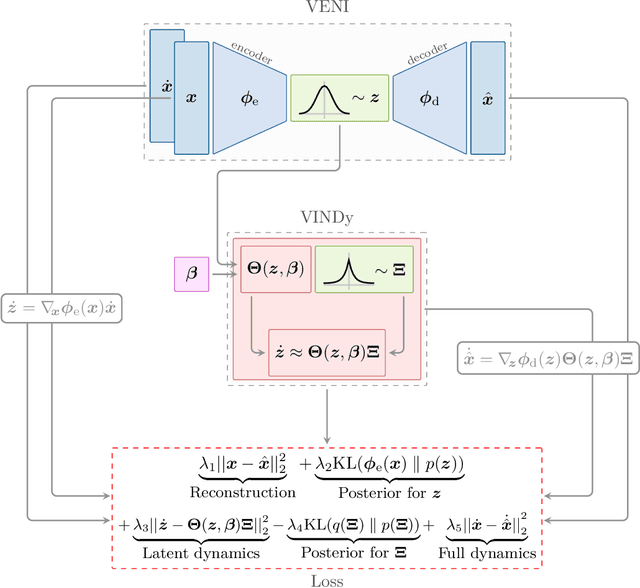
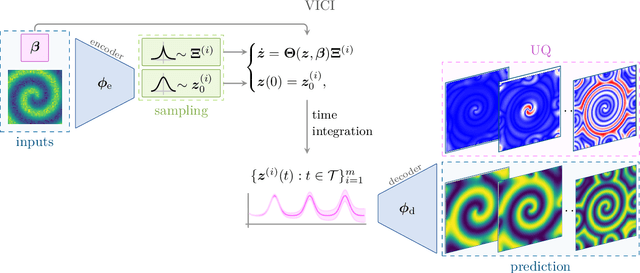
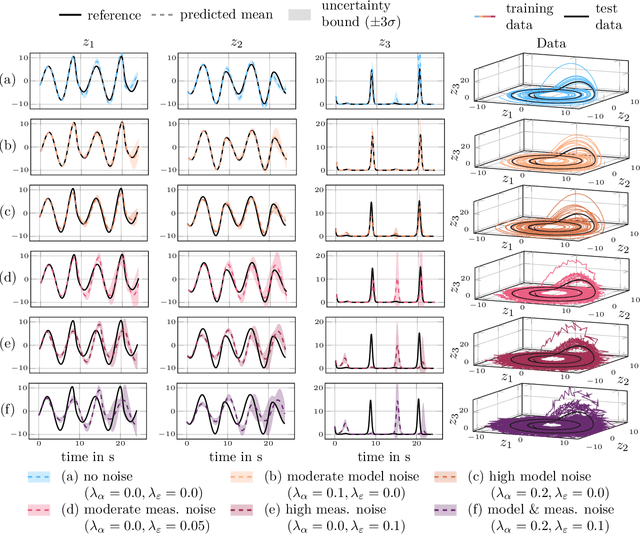
The simulation of many complex phenomena in engineering and science requires solving expensive, high-dimensional systems of partial differential equations (PDEs). To circumvent this, reduced-order models (ROMs) have been developed to speed up computations. However, when governing equations are unknown or partially known, typically ROMs lack interpretability and reliability of the predicted solutions. In this work we present a data-driven, non-intrusive framework for building ROMs where the latent variables and dynamics are identified in an interpretable manner and uncertainty is quantified. Starting from a limited amount of high-dimensional, noisy data the proposed framework constructs an efficient ROM by leveraging variational autoencoders for dimensionality reduction along with a newly introduced, variational version of sparse identification of nonlinear dynamics (SINDy), which we refer to as Variational Identification of Nonlinear Dynamics (VINDy). In detail, the method consists of Variational Encoding of Noisy Inputs (VENI) to identify the distribution of reduced coordinates. Simultaneously, we learn the distribution of the coefficients of a pre-determined set of candidate functions by VINDy. Once trained offline, the identified model can be queried for new parameter instances and new initial conditions to compute the corresponding full-time solutions. The probabilistic setup enables uncertainty quantification as the online testing consists of Variational Inference naturally providing Certainty Intervals (VICI). In this work we showcase the effectiveness of the newly proposed VINDy method in identifying interpretable and accurate dynamical system for the R\"ossler system with different noise intensities and sources. Then the performance of the overall method - named VENI, VINDy, VICI - is tested on PDE benchmarks including structural mechanics and fluid dynamics.

On using Machine Learning Algorithms for Motorcycle Collision Detection

Globally, motorcycles attract vast and varied users. However, since the rate of severe injury and fatality in motorcycle accidents far exceeds passenger car accidents, efforts have been directed toward increasing passive safety systems. Impact simulations show that the risk of severe injury or death in the event of a motorcycle-to-car impact can be greatly reduced if the motorcycle is equipped with passive safety measures such as airbags and seat belts. For the passive safety systems to be activated, a collision must be detected within milliseconds for a wide variety of impact configurations, but under no circumstances may it be falsely triggered. For the challenge of reliably detecting impending collisions, this paper presents an investigation towards the applicability of machine learning algorithms. First, a series of simulations of accidents and driving operation is introduced to collect data to train machine learning classification models. Their performance is henceforth assessed and compared via multiple representative and application-oriented criteria.

Multi-Hierarchical Surrogate Learning for Structural Dynamical Crash Simulations Using Graph Convolutional Neural Networks

Crash simulations play an essential role in improving vehicle safety, design optimization, and injury risk estimation. Unfortunately, numerical solutions of such problems using state-of-the-art high-fidelity models require significant computational effort. Conventional data-driven surrogate modeling approaches create low-dimensional embeddings for evolving the dynamics in order to circumvent this computational effort. Most approaches directly operate on high-resolution data obtained from numerical discretization, which is both costly and complicated for mapping the flow of information over large spatial distances. Furthermore, working with a fixed resolution prevents the adaptation of surrogate models to environments with variable computing capacities, different visualization resolutions, and different accuracy requirements. We thus propose a multi-hierarchical framework for structurally creating a series of surrogate models for a kart frame, which is a good proxy for industrial-relevant crash simulations, at different levels of resolution. For multiscale phenomena, macroscale features are captured on a coarse surrogate, whereas microscale effects are resolved by finer ones. The learned behavior of the individual surrogates is passed from coarse to finer levels through transfer learning. In detail, we perform a mesh simplification on the kart model to obtain multi-resolution representations of it. We then train a graph-convolutional neural network-based surrogate that learns parameter-dependent low-dimensional latent dynamics on the coarsest representation. Subsequently, another, similarly structured surrogate is trained on the residual of the first surrogate using a finer resolution. This step can be repeated multiple times. By doing so, we construct multiple surrogates for the same system with varying hardware requirements and increasing accuracy.

Low-dimensional Data-based Surrogate Model of a Continuum-mechanical Musculoskeletal System Based on Non-intrusive Model Order Reduction

In recent decades, the main focus of computer modeling has been on supporting the design and development of engineering prototyes, but it is now ubiquitous in non-traditional areas such as medical rehabilitation. Conventional modeling approaches like the finite element~(FE) method are computationally costly when dealing with complex models, making them of limited use for purposes like real-time simulation or deployment on low-end hardware, if the model at hand cannot be simplified in a useful manner. Consequently, non-traditional approaches such as surrogate modeling using data-driven model order reduction are used to make complex high-fidelity models more widely available anyway. They often involve a dimensionality reduction step, in which the high-dimensional system state is transformed onto a low-dimensional subspace or manifold, and a regression approach to capture the reduced system behavior. While most publications focus on one dimensionality reduction, such as principal component analysis~(PCA) (linear) or autoencoder (nonlinear), we consider and compare PCA, kernel PCA, autoencoders, as well as variational autoencoders for the approximation of a structural dynamical system. In detail, we demonstrate the benefits of the surrogate modeling approach on a complex FE model of a human upper-arm. We consider both the models deformation and the internal stress as the two main quantities of interest in a FE context. By doing so we are able to create a computationally low cost surrogate model which captures the system behavior with high approximation quality and fast evaluations.

Real-time Human Response Prediction Using a Non-intrusive Data-driven Model Reduction Scheme

Recent research in non-intrusive data-driven model order reduction (MOR) enabled accurate and efficient approximation of parameterized ordinary differential equations (ODEs). However, previous studies have focused on constant parameters, whereas time-dependent parameters have been neglected. The purpose of this paper is to introduce a novel two-step MOR scheme to tackle this issue. In a first step, classic MOR approaches are applied to calculate a low-dimensional representation of high-dimensional ODE solutions, i.e. to extract the most important features of simulation data. Based on this representation, a long short-term memory (LSTM) is trained to predict the reduced dynamics iteratively in a second step. This enables the parameters to be taken into account during the respective time step. The potential of this approach is demonstrated on an occupant model within a car driving scenario. The reduced model's response to time-varying accelerations matches the reference data with high accuracy for a limited amount of time. Furthermore, real-time capability is achieved. Accordingly, it is concluded that the presented method is well suited to approximate parameterized ODEs and can handle time-dependent parameters in contrast to common methods.

Physics-informed Neural Networks-based Model Predictive Control for Multi-link Manipulators

We discuss nonlinear model predictive control (NMPC) for multi-body dynamics via physics-informed machine learning methods. Physics-informed neural networks (PINNs) are a promising tool to approximate (partial) differential equations. PINNs are not suited for control tasks in their original form since they are not designed to handle variable control actions or variable initial values. We thus present the idea of enhancing PINNs by adding control actions and initial conditions as additional network inputs. The high-dimensional input space is subsequently reduced via a sampling strategy and a zero-hold assumption. This strategy enables the controller design based on a PINN as an approximation of the underlying system dynamics. The additional benefit is that the sensitivities are easily computed via automatic differentiation, thus leading to efficient gradient-based algorithms. Finally, we present our results using our PINN-based MPC to solve a tracking problem for a complex mechanical system, a multi-link manipulator.