VENI, VINDy, VICI: a variational reduced-order modeling framework with uncertainty quantification

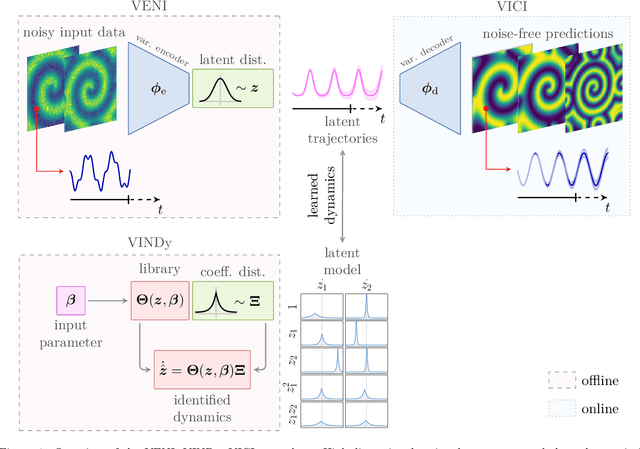
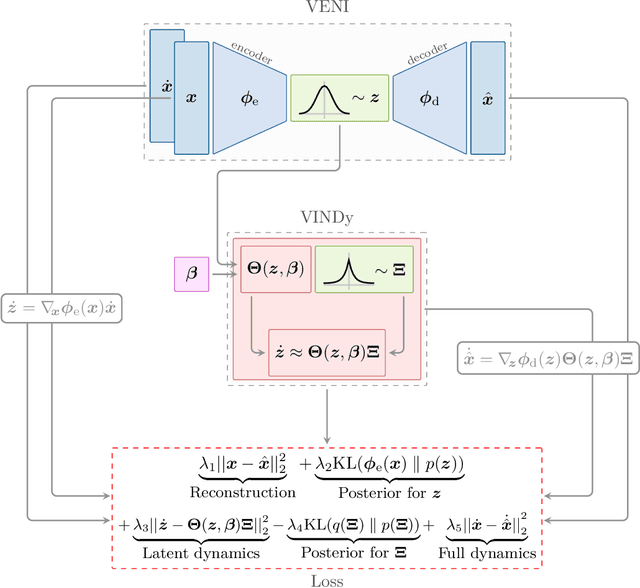
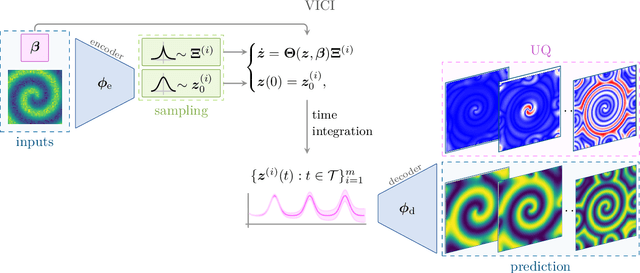
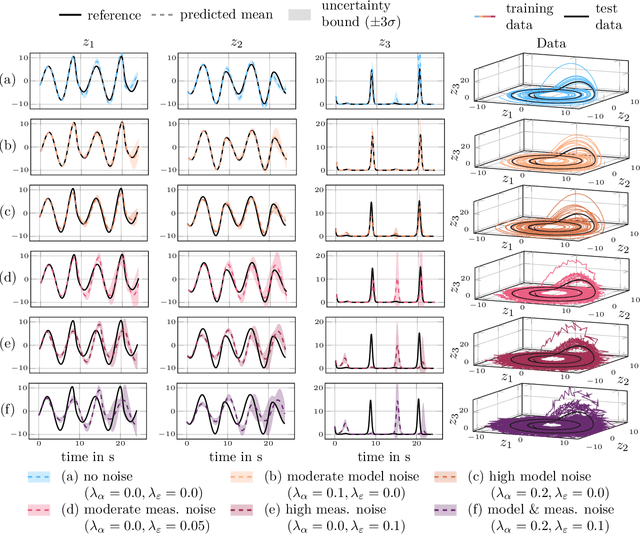
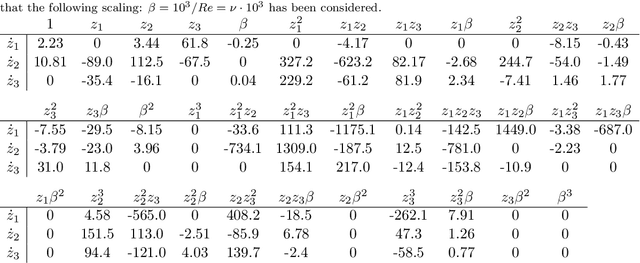
The simulation of many complex phenomena in engineering and science requires solving expensive, high-dimensional systems of partial differential equations (PDEs). To circumvent this, reduced-order models (ROMs) have been developed to speed up computations. However, when governing equations are unknown or partially known, typically ROMs lack interpretability and reliability of the predicted solutions. In this work we present a data-driven, non-intrusive framework for building ROMs where the latent variables and dynamics are identified in an interpretable manner and uncertainty is quantified. Starting from a limited amount of high-dimensional, noisy data the proposed framework constructs an efficient ROM by leveraging variational autoencoders for dimensionality reduction along with a newly introduced, variational version of sparse identification of nonlinear dynamics (SINDy), which we refer to as Variational Identification of Nonlinear Dynamics (VINDy). In detail, the method consists of Variational Encoding of Noisy Inputs (VENI) to identify the distribution of reduced coordinates. Simultaneously, we learn the distribution of the coefficients of a pre-determined set of candidate functions by VINDy. Once trained offline, the identified model can be queried for new parameter instances and new initial conditions to compute the corresponding full-time solutions. The probabilistic setup enables uncertainty quantification as the online testing consists of Variational Inference naturally providing Certainty Intervals (VICI). In this work we showcase the effectiveness of the newly proposed VINDy method in identifying interpretable and accurate dynamical system for the R\"ossler system with different noise intensities and sources. Then the performance of the overall method - named VENI, VINDy, VICI - is tested on PDE benchmarks including structural mechanics and fluid dynamics.

Multi-fidelity reduced-order surrogate modeling

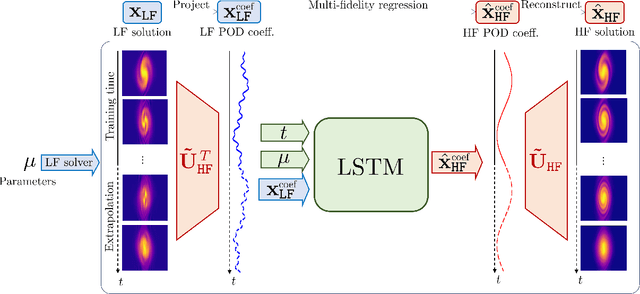
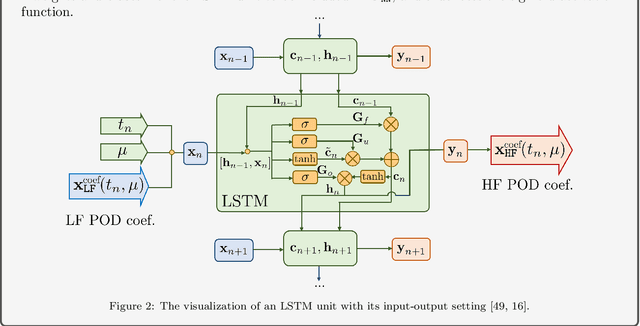
High-fidelity numerical simulations of partial differential equations (PDEs) given a restricted computational budget can significantly limit the number of parameter configurations considered and/or time window evaluated for modeling a given system. Multi-fidelity surrogate modeling aims to leverage less accurate, lower-fidelity models that are computationally inexpensive in order to enhance predictive accuracy when high-fidelity data are limited or scarce. However, low-fidelity models, while often displaying important qualitative spatio-temporal features, fail to accurately capture the onset of instability and critical transients observed in the high-fidelity models, making them impractical as surrogate models. To address this shortcoming, we present a new data-driven strategy that combines dimensionality reduction with multi-fidelity neural network surrogates. The key idea is to generate a spatial basis by applying the classical proper orthogonal decomposition (POD) to high-fidelity solution snapshots, and approximate the dynamics of the reduced states - time-parameter-dependent expansion coefficients of the POD basis - using a multi-fidelity long-short term memory (LSTM) network. By mapping low-fidelity reduced states to their high-fidelity counterpart, the proposed reduced-order surrogate model enables the efficient recovery of full solution fields over time and parameter variations in a non-intrusive manner. The generality and robustness of this method is demonstrated by a collection of parametrized, time-dependent PDE problems where the low-fidelity model can be defined by coarser meshes and/or time stepping, as well as by misspecified physical features. Importantly, the onset of instabilities and transients are well captured by this surrogate modeling technique.

Reduced order modeling of parametrized systems through autoencoders and SINDy approach: continuation of periodic solutions

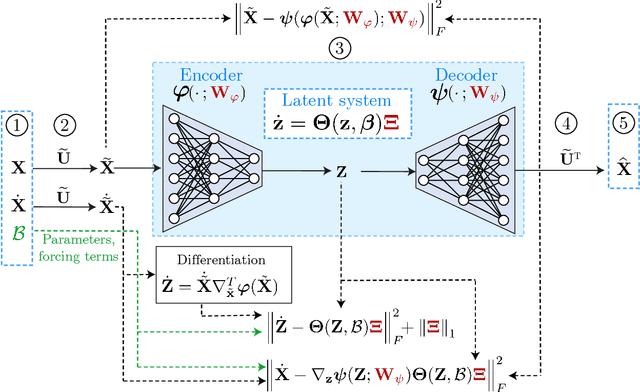
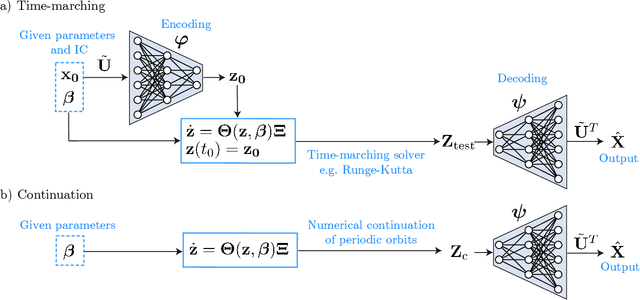
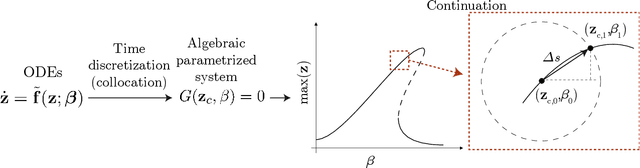
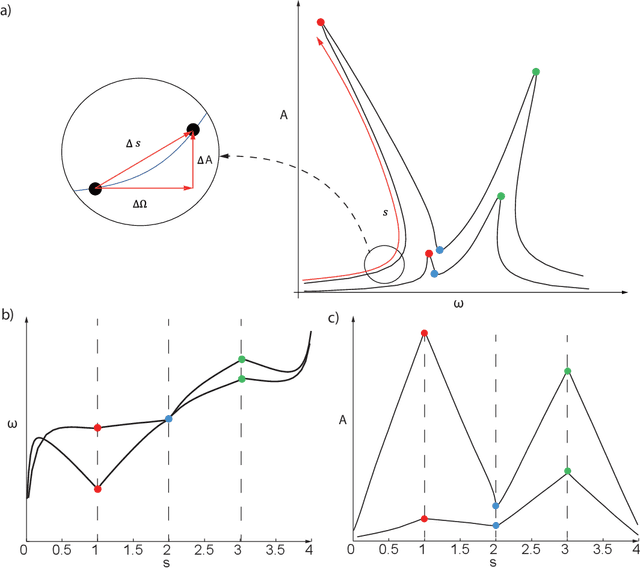
Highly accurate simulations of complex phenomena governed by partial differential equations (PDEs) typically require intrusive methods and entail expensive computational costs, which might become prohibitive when approximating steady-state solutions of PDEs for multiple combinations of control parameters and initial conditions. Therefore, constructing efficient reduced order models (ROMs) that enable accurate but fast predictions, while retaining the dynamical characteristics of the physical phenomenon as parameters vary, is of paramount importance. In this work, a data-driven, non-intrusive framework which combines ROM construction with reduced dynamics identification, is presented. Starting from a limited amount of full order solutions, the proposed approach leverages autoencoder neural networks with parametric sparse identification of nonlinear dynamics (SINDy) to construct a low-dimensional dynamical model which can be queried to efficiently compute full-time solutions at new parameter instances, as well as directly fed to continuation algorithms. These latter aim at tracking the evolution of periodic steady-state responses as functions of system parameters, avoiding the computation of the transient phase, and allowing to detect instabilities and bifurcations. Featuring an explicit and parametrized modeling of the reduced dynamics, the proposed data-driven framework presents remarkable capabilities to generalize both with respect to time and parameters. Applications to structural mechanics and fluid dynamics problems illustrate the effectiveness and accuracy of the method.

Virtual twins of nonlinear vibrating multiphysics microstructures: physics-based versus deep learning-based approaches

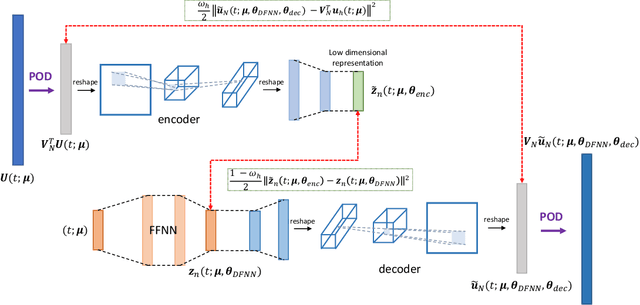
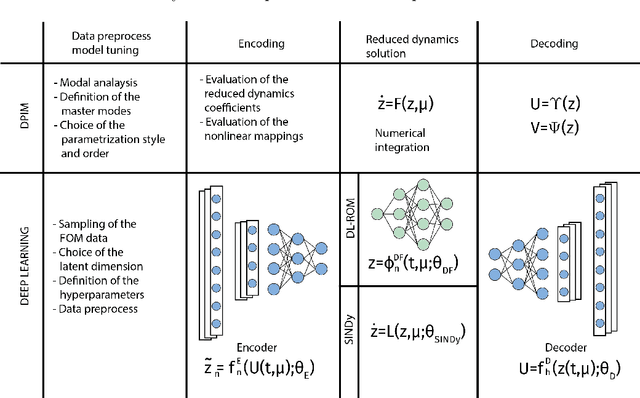
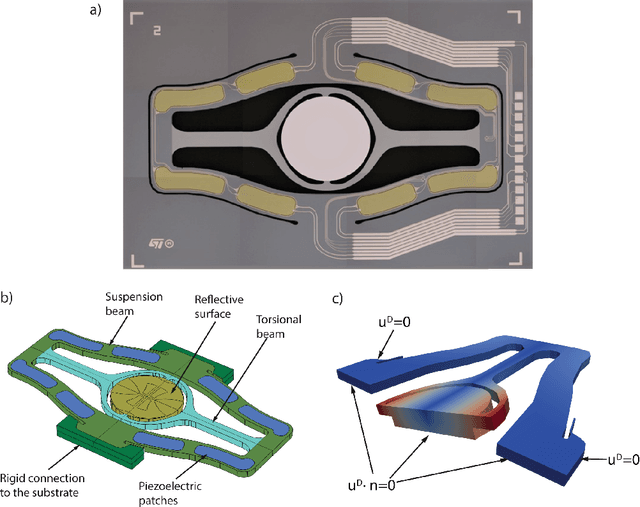
Micro-Electro-Mechanical-Systems are complex structures, often involving nonlinearites of geometric and multiphysics nature, that are used as sensors and actuators in countless applications. Starting from full-order representations, we apply deep learning techniques to generate accurate, efficient and real-time reduced order models to be used as virtual twin for the simulation and optimization of higher-level complex systems. We extensively test the reliability of the proposed procedures on micromirrors, arches and gyroscopes, also displaying intricate dynamical evolutions like internal resonances. In particular, we discuss the accuracy of the deep learning technique and its ability to replicate and converge to the invariant manifolds predicted using the recently developed direct parametrization approach that allows extracting the nonlinear normal modes of large finite element models. Finally, by addressing an electromechanical gyroscope, we show that the non-intrusive deep learning approach generalizes easily to complex multiphysics problems