Stefania Fresca
Explainable Deep Learning-based Classification of Wolff-Parkinson-White Electrocardiographic Signals
Nov 08, 2025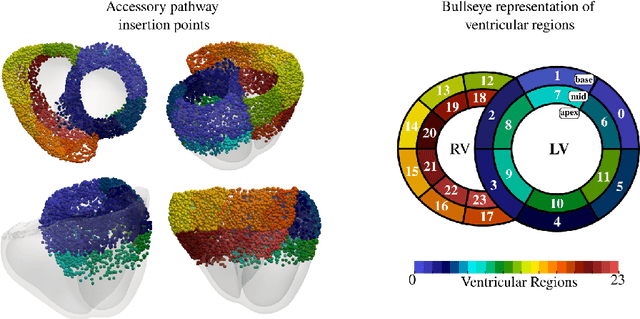
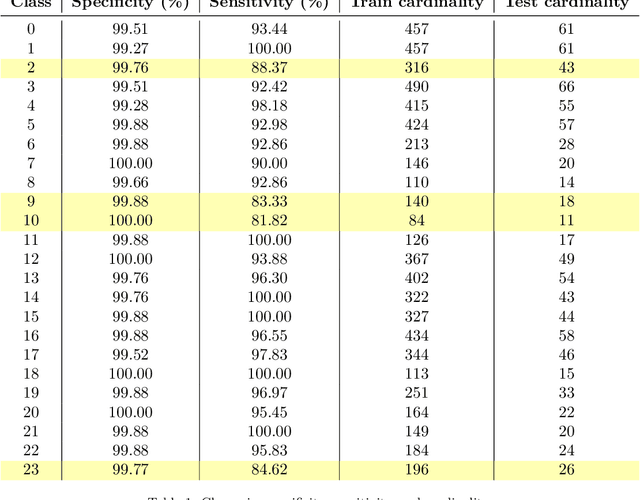
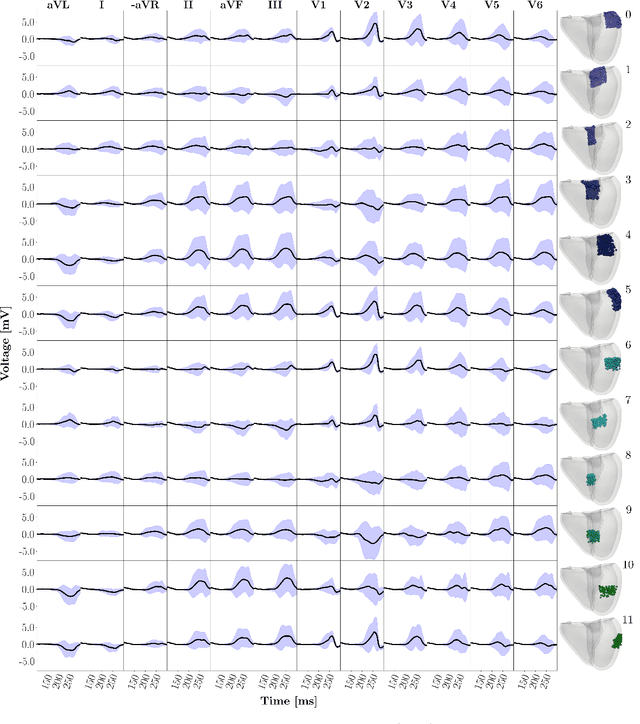
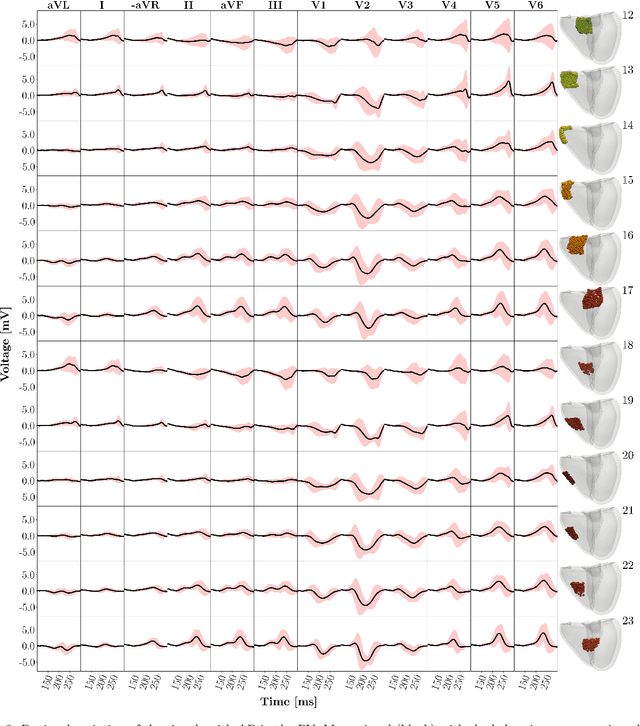
Abstract:Wolff-Parkinson-White (WPW) syndrome is a cardiac electrophysiology (EP) disorder caused by the presence of an accessory pathway (AP) that bypasses the atrioventricular node, faster ventricular activation rate, and provides a substrate for atrio-ventricular reentrant tachycardia (AVRT). Accurate localization of the AP is critical for planning and guiding catheter ablation procedures. While traditional diagnostic tree (DT) methods and more recent machine learning (ML) approaches have been proposed to predict AP location from surface electrocardiogram (ECG), they are often constrained by limited anatomical localization resolution, poor interpretability, and the use of small clinical datasets. In this study, we present a Deep Learning (DL) model for the localization of single manifest APs across 24 cardiac regions, trained on a large, physiologically realistic database of synthetic ECGs generated using a personalized virtual heart model. We also integrate eXplainable Artificial Intelligence (XAI) methods, Guided Backpropagation, Grad-CAM, and Guided Grad-CAM, into the pipeline. This enables interpretation of DL decision-making and addresses one of the main barriers to clinical adoption: lack of transparency in ML predictions. Our model achieves localization accuracy above 95%, with a sensitivity of 94.32% and specificity of 99.78%. XAI outputs are physiologically validated against known depolarization patterns, and a novel index is introduced to identify the most informative ECG leads for AP localization. Results highlight lead V2 as the most critical, followed by aVF, V1, and aVL. This work demonstrates the potential of combining cardiac digital twins with explainable DL to enable accurate, transparent, and non-invasive AP localization.
Multi-Level Monte Carlo Training of Neural Operators
May 19, 2025Abstract:Operator learning is a rapidly growing field that aims to approximate nonlinear operators related to partial differential equations (PDEs) using neural operators. These rely on discretization of input and output functions and are, usually, expensive to train for large-scale problems at high-resolution. Motivated by this, we present a Multi-Level Monte Carlo (MLMC) approach to train neural operators by leveraging a hierarchy of resolutions of function dicretization. Our framework relies on using gradient corrections from fewer samples of fine-resolution data to decrease the computational cost of training while maintaining a high level accuracy. The proposed MLMC training procedure can be applied to any architecture accepting multi-resolution data. Our numerical experiments on a range of state-of-the-art models and test-cases demonstrate improved computational efficiency compared to traditional single-resolution training approaches, and highlight the existence of a Pareto curve between accuracy and computational time, related to the number of samples per resolution.
Integrating Fourier Neural Operators with Diffusion Models to improve Spectral Representation of Synthetic Earthquake Ground Motion Response
Apr 01, 2025Abstract:Nuclear reactor buildings must be designed to withstand the dynamic load induced by strong ground motion earthquakes. For this reason, their structural behavior must be assessed in multiple realistic ground shaking scenarios (e.g., the Maximum Credible Earthquake). However, earthquake catalogs and recorded seismograms may not always be available in the region of interest. Therefore, synthetic earthquake ground motion is progressively being employed, although with some due precautions: earthquake physics is sometimes not well enough understood to be accurately reproduced with numerical tools, and the underlying epistemic uncertainties lead to prohibitive computational costs related to model calibration. In this study, we propose an AI physics-based approach to generate synthetic ground motion, based on the combination of a neural operator that approximates the elastodynamics Green's operator in arbitrary source-geology setups, enhanced by a denoising diffusion probabilistic model. The diffusion model is trained to correct the ground motion time series generated by the neural operator. Our results show that such an approach promisingly enhances the realism of the generated synthetic seismograms, with frequency biases and Goodness-Of-Fit (GOF) scores being improved by the diffusion model. This indicates that the latter is capable to mitigate the mid-frequency spectral falloff observed in the time series generated by the neural operator. Our method showcases fast and cheap inference in different site and source conditions.
Beyond Interpolation: Extrapolative Reasoning with Reinforcement Learning and Graph Neural Networks
Feb 06, 2025



Abstract:Despite incredible progress, many neural architectures fail to properly generalize beyond their training distribution. As such, learning to reason in a correct and generalizable way is one of the current fundamental challenges in machine learning. In this respect, logic puzzles provide a great testbed, as we can fully understand and control the learning environment. Thus, they allow to evaluate performance on previously unseen, larger and more difficult puzzles that follow the same underlying rules. Since traditional approaches often struggle to represent such scalable logical structures, we propose to model these puzzles using a graph-based approach. Then, we investigate the key factors enabling the proposed models to learn generalizable solutions in a reinforcement learning setting. Our study focuses on the impact of the inductive bias of the architecture, different reward systems and the role of recurrent modeling in enabling sequential reasoning. Through extensive experiments, we demonstrate how these elements contribute to successful extrapolation on increasingly complex puzzles.These insights and frameworks offer a systematic way to design learning-based systems capable of generalizable reasoning beyond interpolation.
HypeRL: Parameter-Informed Reinforcement Learning for Parametric PDEs
Jan 08, 2025



Abstract:In this work, we devise a new, general-purpose reinforcement learning strategy for the optimal control of parametric partial differential equations (PDEs). Such problems frequently arise in applied sciences and engineering and entail a significant complexity when control and/or state variables are distributed in high-dimensional space or depend on varying parameters. Traditional numerical methods, relying on either iterative minimization algorithms or dynamic programming, while reliable, often become computationally infeasible. Indeed, in either way, the optimal control problem must be solved for each instance of the parameters, and this is out of reach when dealing with high-dimensional time-dependent and parametric PDEs. In this paper, we propose HypeRL, a deep reinforcement learning (DRL) framework to overcome the limitations shown by traditional methods. HypeRL aims at approximating the optimal control policy directly. Specifically, we employ an actor-critic DRL approach to learn an optimal feedback control strategy that can generalize across the range of variation of the parameters. To effectively learn such optimal control laws, encoding the parameter information into the DRL policy and value function neural networks (NNs) is essential. To do so, HypeRL uses two additional NNs, often called hypernetworks, to learn the weights and biases of the value function and the policy NNs. We validate the proposed approach on two PDE-constrained optimal control benchmarks, namely a 1D Kuramoto-Sivashinsky equation and a 2D Navier-Stokes equations, by showing that the knowledge of the PDE parameters and how this information is encoded, i.e., via a hypernetwork, is an essential ingredient for learning parameter-dependent control policies that can generalize effectively to unseen scenarios and for improving the sample efficiency of such policies.
Handling geometrical variability in nonlinear reduced order modeling through Continuous Geometry-Aware DL-ROMs
Nov 08, 2024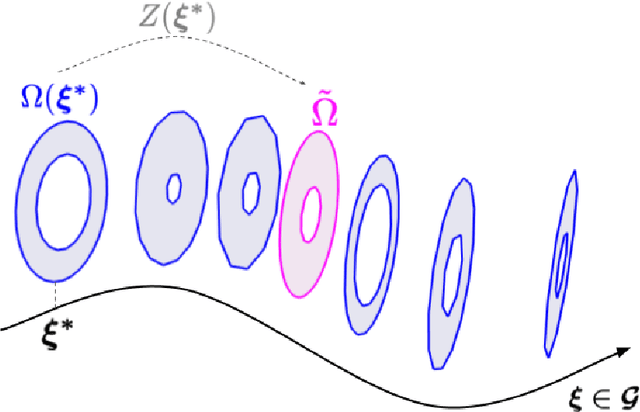

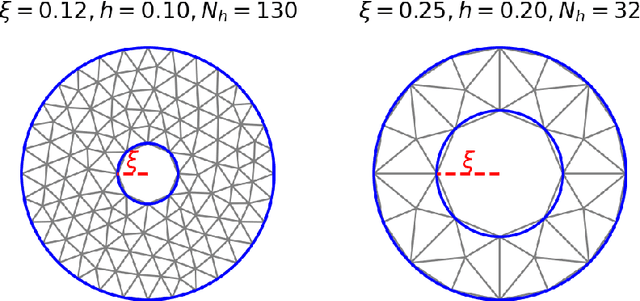
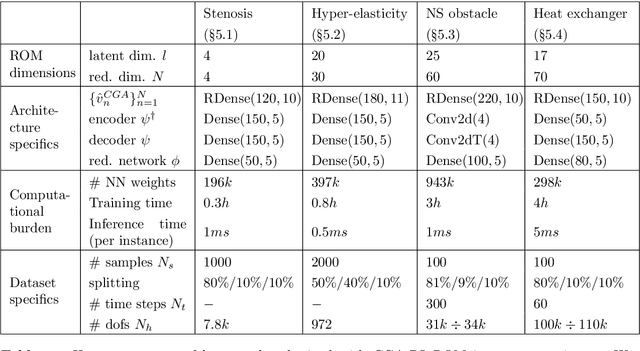
Abstract:Deep Learning-based Reduced Order Models (DL-ROMs) provide nowadays a well-established class of accurate surrogate models for complex physical systems described by parametrized PDEs, by nonlinearly compressing the solution manifold into a handful of latent coordinates. Until now, design and application of DL-ROMs mainly focused on physically parameterized problems. Within this work, we provide a novel extension of these architectures to problems featuring geometrical variability and parametrized domains, namely, we propose Continuous Geometry-Aware DL-ROMs (CGA-DL-ROMs). In particular, the space-continuous nature of the proposed architecture matches the need to deal with multi-resolution datasets, which are quite common in the case of geometrically parametrized problems. Moreover, CGA-DL-ROMs are endowed with a strong inductive bias that makes them aware of geometrical parametrizations, thus enhancing both the compression capability and the overall performance of the architecture. Within this work, we justify our findings through a thorough theoretical analysis, and we practically validate our claims by means of a series of numerical tests encompassing physically-and-geometrically parametrized PDEs, ranging from the unsteady Navier-Stokes equations for fluid dynamics to advection-diffusion-reaction equations for mathematical biology.
On latent dynamics learning in nonlinear reduced order modeling
Aug 27, 2024



Abstract:In this work, we present the novel mathematical framework of latent dynamics models (LDMs) for reduced order modeling of parameterized nonlinear time-dependent PDEs. Our framework casts this latter task as a nonlinear dimensionality reduction problem, while constraining the latent state to evolve accordingly to an (unknown) dynamical system. A time-continuous setting is employed to derive error and stability estimates for the LDM approximation of the full order model (FOM) solution. We analyze the impact of using an explicit Runge-Kutta scheme in the time-discrete setting, resulting in the $\Delta\text{LDM}$ formulation, and further explore the learnable setting, $\Delta\text{LDM}_\theta$, where deep neural networks approximate the discrete LDM components, while providing a bounded approximation error with respect to the FOM. Moreover, we extend the concept of parameterized Neural ODE - recently proposed as a possible way to build data-driven dynamical systems with varying input parameters - to be a convolutional architecture, where the input parameters information is injected by means of an affine modulation mechanism, while designing a convolutional autoencoder neural network able to retain spatial-coherence, thus enhancing interpretability at the latent level. Numerical experiments, including the Burgers' and the advection-reaction-diffusion equations, demonstrate the framework's ability to obtain, in a multi-query context, a time-continuous approximation of the FOM solution, thus being able to query the LDM approximation at any given time instance while retaining a prescribed level of accuracy. Our findings highlight the remarkable potential of the proposed LDMs, representing a mathematically rigorous framework to enhance the accuracy and approximation capabilities of reduced order modeling for time-dependent parameterized PDEs.
PTPI-DL-ROMs: pre-trained physics-informed deep learning-based reduced order models for nonlinear parametrized PDEs
May 14, 2024



Abstract:The coupling of Proper Orthogonal Decomposition (POD) and deep learning-based ROMs (DL-ROMs) has proved to be a successful strategy to construct non-intrusive, highly accurate, surrogates for the real time solution of parametric nonlinear time-dependent PDEs. Inexpensive to evaluate, POD-DL-ROMs are also relatively fast to train, thanks to their limited complexity. However, POD-DL-ROMs account for the physical laws governing the problem at hand only through the training data, that are usually obtained through a full order model (FOM) relying on a high-fidelity discretization of the underlying equations. Moreover, the accuracy of POD-DL-ROMs strongly depends on the amount of available data. In this paper, we consider a major extension of POD-DL-ROMs by enforcing the fulfillment of the governing physical laws in the training process -- that is, by making them physics-informed -- to compensate for possible scarce and/or unavailable data and improve the overall reliability. To do that, we first complement POD-DL-ROMs with a trunk net architecture, endowing them with the ability to compute the problem's solution at every point in the spatial domain, and ultimately enabling a seamless computation of the physics-based loss by means of the strong continuous formulation. Then, we introduce an efficient training strategy that limits the notorious computational burden entailed by a physics-informed training phase. In particular, we take advantage of the few available data to develop a low-cost pre-training procedure; then, we fine-tune the architecture in order to further improve the prediction reliability. Accuracy and efficiency of the resulting pre-trained physics-informed DL-ROMs (PTPI-DL-ROMs) are then assessed on a set of test cases ranging from non-affinely parametrized advection-diffusion-reaction equations, to nonlinear problems like the Navier-Stokes equations for fluid flows.
Deep Learning-based surrogate models for parametrized PDEs: handling geometric variability through graph neural networks
Aug 03, 2023Abstract:Mesh-based simulations play a key role when modeling complex physical systems that, in many disciplines across science and engineering, require the solution of parametrized time-dependent nonlinear partial differential equations (PDEs). In this context, full order models (FOMs), such as those relying on the finite element method, can reach high levels of accuracy, however often yielding intensive simulations to run. For this reason, surrogate models are developed to replace computationally expensive solvers with more efficient ones, which can strike favorable trade-offs between accuracy and efficiency. This work explores the potential usage of graph neural networks (GNNs) for the simulation of time-dependent PDEs in the presence of geometrical variability. In particular, we propose a systematic strategy to build surrogate models based on a data-driven time-stepping scheme where a GNN architecture is used to efficiently evolve the system. With respect to the majority of surrogate models, the proposed approach stands out for its ability of tackling problems with parameter dependent spatial domains, while simultaneously generalizing to different geometries and mesh resolutions. We assess the effectiveness of the proposed approach through a series of numerical experiments, involving both two- and three-dimensional problems, showing that GNNs can provide a valid alternative to traditional surrogate models in terms of computational efficiency and generalization to new scenarios. We also assess, from a numerical standpoint, the importance of using GNNs, rather than classical dense deep neural networks, for the proposed framework.
Reduced order modeling of parametrized systems through autoencoders and SINDy approach: continuation of periodic solutions
Nov 13, 2022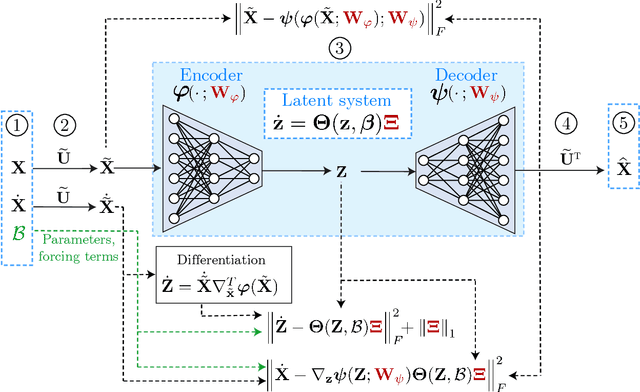
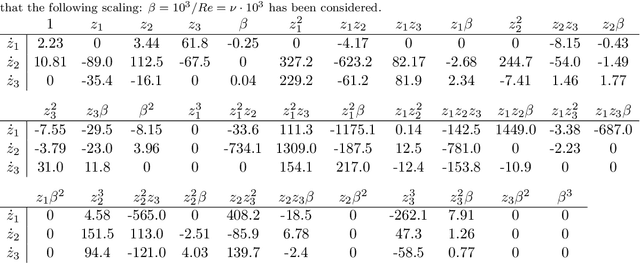
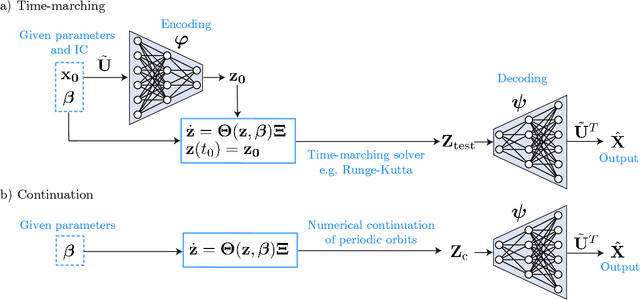
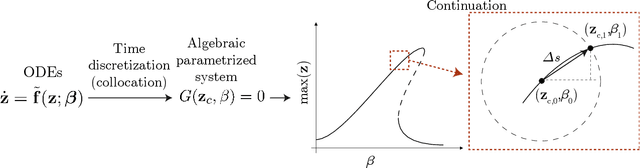
Abstract:Highly accurate simulations of complex phenomena governed by partial differential equations (PDEs) typically require intrusive methods and entail expensive computational costs, which might become prohibitive when approximating steady-state solutions of PDEs for multiple combinations of control parameters and initial conditions. Therefore, constructing efficient reduced order models (ROMs) that enable accurate but fast predictions, while retaining the dynamical characteristics of the physical phenomenon as parameters vary, is of paramount importance. In this work, a data-driven, non-intrusive framework which combines ROM construction with reduced dynamics identification, is presented. Starting from a limited amount of full order solutions, the proposed approach leverages autoencoder neural networks with parametric sparse identification of nonlinear dynamics (SINDy) to construct a low-dimensional dynamical model which can be queried to efficiently compute full-time solutions at new parameter instances, as well as directly fed to continuation algorithms. These latter aim at tracking the evolution of periodic steady-state responses as functions of system parameters, avoiding the computation of the transient phase, and allowing to detect instabilities and bifurcations. Featuring an explicit and parametrized modeling of the reduced dynamics, the proposed data-driven framework presents remarkable capabilities to generalize both with respect to time and parameters. Applications to structural mechanics and fluid dynamics problems illustrate the effectiveness and accuracy of the method.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge