Fine-Tuning Discrete Diffusion Models with Policy Gradient Methods

Discrete diffusion models have recently gained significant attention due to their ability to process complex discrete structures for language modeling. However, fine-tuning these models with policy gradient methods, as is commonly done in Reinforcement Learning from Human Feedback (RLHF), remains a challenging task. We propose an efficient, broadly applicable, and theoretically justified policy gradient algorithm, called Score Entropy Policy Optimization (SEPO), for fine-tuning discrete diffusion models over non-differentiable rewards. Our numerical experiments across several discrete generative tasks demonstrate the scalability and efficiency of our method. Our code is available at https://github.com/ozekri/SEPO

Operator learning regularization for macroscopic permeability prediction in dual-scale flow problem

Liquid composites moulding is an important manufacturing technology for fibre reinforced composites, due to its cost-effectiveness. Challenges lie in the optimisation of the process due to the lack of understanding of key characteristic of textile fabrics - permeability. The problem of computing the permeability coefficient can be modelled as the well-known Stokes-Brinkman equation, which introduces a heterogeneous parameter $\beta$ distinguishing macropore regions and fibre-bundle regions. In the present work, we train a Fourier neural operator to learn the nonlinear map from the heterogeneous coefficient $\beta$ to the velocity field $u$, and recover the corresponding macroscopic permeability $K$. This is a challenging inverse problem since both the input and output fields span several order of magnitudes, we introduce different regularization techniques for the loss function and perform a quantitative comparison between them.

Density estimation with LLMs: a geometric investigation of in-context learning trajectories

Large language models (LLMs) demonstrate remarkable emergent abilities to perform in-context learning across various tasks, including time series forecasting. This work investigates LLMs' ability to estimate probability density functions (PDFs) from data observed in-context; such density estimation (DE) is a fundamental task underlying many probabilistic modeling problems. We leverage the Intensive Principal Component Analysis (InPCA) to visualize and analyze the in-context learning dynamics of LLaMA-2 models. Our main finding is that these LLMs all follow similar learning trajectories in a low-dimensional InPCA space, which are distinct from those of traditional density estimation methods like histograms and Gaussian kernel density estimation (KDE). We interpret the LLaMA in-context DE process as a KDE with an adaptive kernel width and shape. This custom kernel model captures a significant portion of LLaMA's behavior despite having only two parameters. We further speculate on why LLaMA's kernel width and shape differs from classical algorithms, providing insights into the mechanism of in-context probabilistic reasoning in LLMs.

Large Language Models as Markov Chains

Large language models (LLMs) have proven to be remarkably efficient, both across a wide range of natural language processing tasks and well beyond them. However, a comprehensive theoretical analysis of the origins of their impressive performance remains elusive. In this paper, we approach this challenging task by drawing an equivalence between generic autoregressive language models with vocabulary of size $T$ and context window of size $K$ and Markov chains defined on a finite state space of size $\mathcal{O}(T^K)$. We derive several surprising findings related to the existence of a stationary distribution of Markov chains that capture the inference power of LLMs, their speed of convergence to it, and the influence of the temperature on the latter. We then prove pre-training and in-context generalization bounds and show how the drawn equivalence allows us to enrich their interpretation. Finally, we illustrate our theoretical guarantees with experiments on several recent LLMs to highlight how they capture the behavior observed in practice.

Lines of Thought in Large Language Models

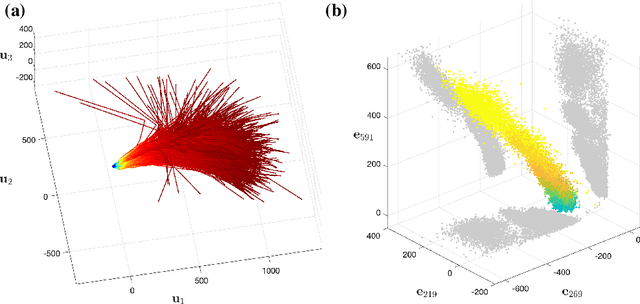
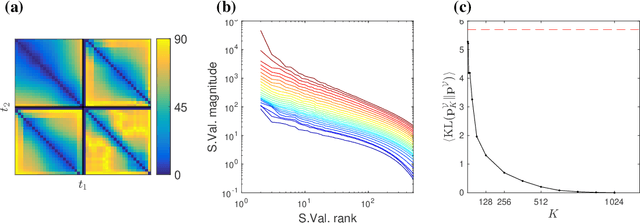
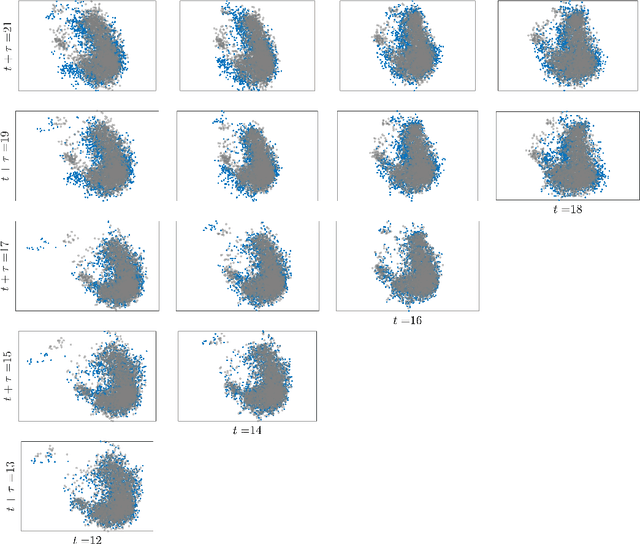
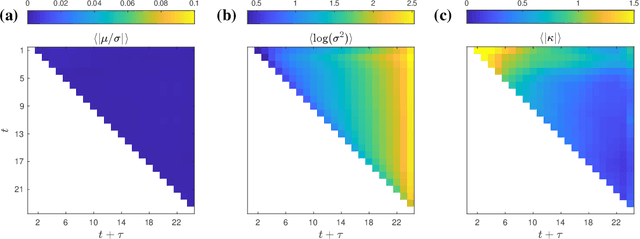
Large Language Models achieve next-token prediction by transporting a vectorized piece of text (prompt) across an accompanying embedding space under the action of successive transformer layers. The resulting high-dimensional trajectories realize different contextualization, or 'thinking', steps, and fully determine the output probability distribution. We aim to characterize the statistical properties of ensembles of these 'lines of thought.' We observe that independent trajectories cluster along a low-dimensional, non-Euclidean manifold, and that their path can be well approximated by a stochastic equation with few parameters extracted from data. We find it remarkable that the vast complexity of such large models can be reduced to a much simpler form, and we reflect on implications.

Structure-Preserving Operator Learning

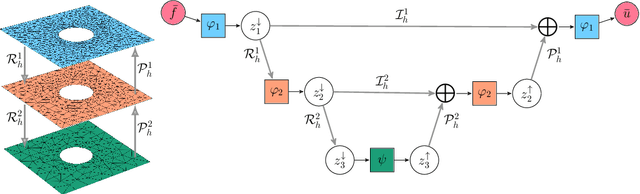
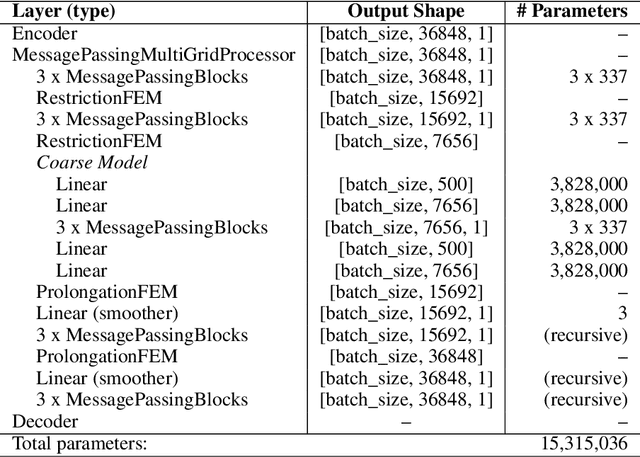
Learning complex dynamics driven by partial differential equations directly from data holds great promise for fast and accurate simulations of complex physical systems. In most cases, this problem can be formulated as an operator learning task, where one aims to learn the operator representing the physics of interest, which entails discretization of the continuous system. However, preserving key continuous properties at the discrete level, such as boundary conditions, and addressing physical systems with complex geometries is challenging for most existing approaches. We introduce a family of operator learning architectures, structure-preserving operator networks (SPONs), that allows to preserve key mathematical and physical properties of the continuous system by leveraging finite element (FE) discretizations of the input-output spaces. SPONs are encode-process-decode architectures that are end-to-end differentiable, where the encoder and decoder follows from the discretizations of the input-output spaces. SPONs can operate on complex geometries, enforce certain boundary conditions exactly, and offer theoretical guarantees. Our framework provides a flexible way of devising structure-preserving architectures tailored to specific applications, and offers an explicit trade-off between performance and efficiency, all thanks to the FE discretization of the input-output spaces. Additionally, we introduce a multigrid-inspired SPON architecture that yields improved performance at higher efficiency. Finally, we release a software to automate the design and training of SPON architectures.

Multiplicative Dynamic Mode Decomposition

Koopman operators are infinite-dimensional operators that linearize nonlinear dynamical systems, facilitating the study of their spectral properties and enabling the prediction of the time evolution of observable quantities. Recent methods have aimed to approximate Koopman operators while preserving key structures. However, approximating Koopman operators typically requires a dictionary of observables to capture the system's behavior in a finite-dimensional subspace. The selection of these functions is often heuristic, may result in the loss of spectral information, and can severely complicate structure preservation. This paper introduces Multiplicative Dynamic Mode Decomposition (MultDMD), which enforces the multiplicative structure inherent in the Koopman operator within its finite-dimensional approximation. Leveraging this multiplicative property, we guide the selection of observables and define a constrained optimization problem for the matrix approximation, which can be efficiently solved. MultDMD presents a structured approach to finite-dimensional approximations and can more accurately reflect the spectral properties of the Koopman operator. We elaborate on the theoretical framework of MultDMD, detailing its formulation, optimization strategy, and convergence properties. The efficacy of MultDMD is demonstrated through several examples, including the nonlinear pendulum, the Lorenz system, and fluid dynamics data, where we demonstrate its remarkable robustness to noise.

LLMs learn governing principles of dynamical systems, revealing an in-context neural scaling law

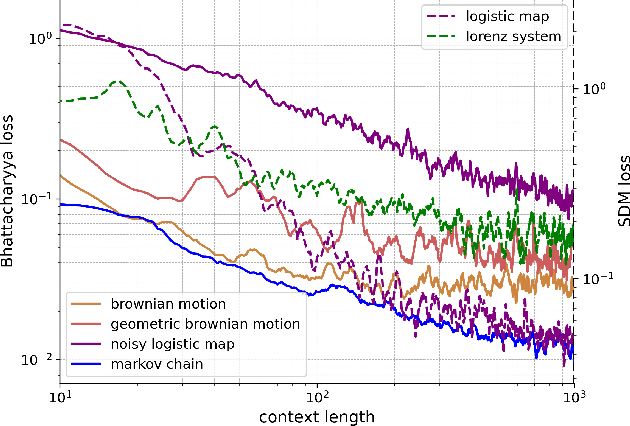
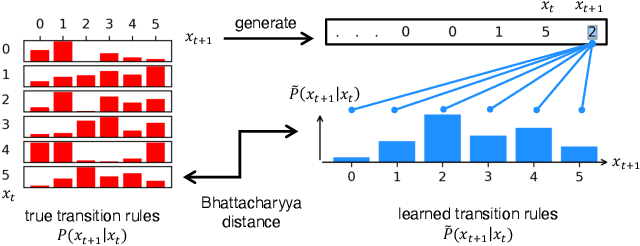
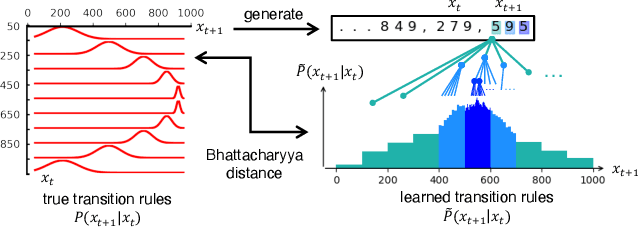
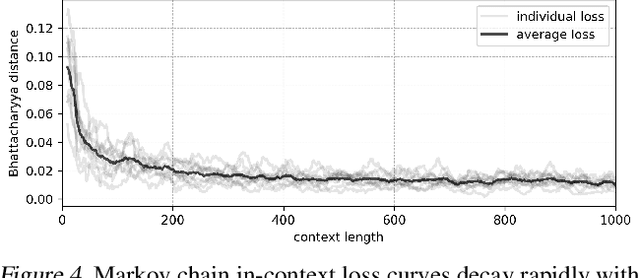
Pretrained large language models (LLMs) are surprisingly effective at performing zero-shot tasks, including time-series forecasting. However, understanding the mechanisms behind such capabilities remains highly challenging due to the complexity of the models. In this paper, we study LLMs' ability to extrapolate the behavior of dynamical systems whose evolution is governed by principles of physical interest. Our results show that LLaMA 2, a language model trained primarily on texts, achieves accurate predictions of dynamical system time series without fine-tuning or prompt engineering. Moreover, the accuracy of the learned physical rules increases with the length of the input context window, revealing an in-context version of neural scaling law. Along the way, we present a flexible and efficient algorithm for extracting probability density functions of multi-digit numbers directly from LLMs.

Operator learning without the adjoint

There is a mystery at the heart of operator learning: how can one recover a non-self-adjoint operator from data without probing the adjoint? Current practical approaches suggest that one can accurately recover an operator while only using data generated by the forward action of the operator without access to the adjoint. However, naively, it seems essential to sample the action of the adjoint. In this paper, we partially explain this mystery by proving that without querying the adjoint, one can approximate a family of non-self-adjoint infinite-dimensional compact operators via projection onto a Fourier basis. We then apply the result to recovering Green's functions of elliptic partial differential operators and derive an adjoint-free sample complexity bound. While existing theory justifies low sample complexity in operator learning, ours is the first adjoint-free analysis that attempts to close the gap between theory and practice.

On the Convergence of Hermitian Dynamic Mode Decomposition

In this work, we study the convergence of Hermitian Dynamic Mode Decomposition (DMD) to the spectral properties of self-adjoint Koopman operators. Hermitian DMD is a data-driven method for approximating the Koopman operator associated with an unknown nonlinear dynamical system from discrete-time snapshots, while preserving the self-adjointness of the operator on its finite-dimensional approximations. We show that, under suitable conditions, the eigenvalues and eigenfunctions of HDMD converge to the spectral properties of the underlying Koopman operator. Along the way, we establish a general theorem on the convergence of spectral measures, and demonstrate our results numerically on the two-dimensional Schr\"odinger equation.