Avoiding spectral pollution for transfer operators using residuals

Koopman operator theory enables linear analysis of nonlinear dynamical systems by lifting their evolution to infinite-dimensional function spaces. However, finite-dimensional approximations of Koopman and transfer (Frobenius--Perron) operators are prone to spectral pollution, introducing spurious eigenvalues that can compromise spectral computations. While recent advances have yielded provably convergent methods for Koopman operators, analogous tools for general transfer operators remain limited. In this paper, we present algorithms for computing spectral properties of transfer operators without spectral pollution, including extensions to the Hardy-Hilbert space. Case studies--ranging from families of Blaschke maps with known spectrum to a molecular dynamics model of protein folding--demonstrate the accuracy and flexibility of our approach. Notably, we demonstrate that spectral features can arise even when the corresponding eigenfunctions lie outside the chosen space, highlighting the functional-analytic subtleties in defining the "true" Koopman spectrum. Our methods offer robust tools for spectral estimation across a broad range of applications.

Deep greedy unfolding: Sorting out argsorting in greedy sparse recovery algorithms

Gradient-based learning imposes (deep) neural networks to be differentiable at all steps. This includes model-based architectures constructed by unrolling iterations of an iterative algorithm onto layers of a neural network, known as algorithm unrolling. However, greedy sparse recovery algorithms depend on the non-differentiable argsort operator, which hinders their integration into neural networks. In this paper, we address this challenge in Orthogonal Matching Pursuit (OMP) and Iterative Hard Thresholding (IHT), two popular representative algorithms in this class. We propose permutation-based variants of these algorithms and approximate permutation matrices using "soft" permutation matrices derived from softsort, a continuous relaxation of argsort. We demonstrate -- both theoretically and numerically -- that Soft-OMP and Soft-IHT, as differentiable counterparts of OMP and IHT and fully compatible with neural network training, effectively approximate these algorithms with a controllable degree of accuracy. This leads to the development of OMP- and IHT-Net, fully trainable network architectures based on Soft-OMP and Soft-IHT, respectively. Finally, by choosing weights as "structure-aware" trainable parameters, we connect our approach to structured sparse recovery and demonstrate its ability to extract latent sparsity patterns from data.

A Novel Use of Pseudospectra in Mathematical Biology: Understanding HPA Axis Sensitivity

The Hypothalamic-Pituitary-Adrenal (HPA) axis is a major neuroendocrine system, and its dysregulation is implicated in various diseases. This system also presents interesting mathematical challenges for modeling. We consider a nonlinear delay differential equation model and calculate pseudospectra of three different linearizations: a time-dependent Jacobian, linearization around the limit cycle, and dynamic mode decomposition (DMD) analysis of Koopman operators (global linearization). The time-dependent Jacobian provided insight into experimental phenomena, explaining why rats respond differently to perturbations during corticosterone secretion's upward versus downward slopes. We developed new mathematical techniques for the other two linearizations to calculate pseudospectra on Banach spaces and apply DMD to delay differential equations, respectively. These methods helped establish local and global limit cycle stability and study transients. Additionally, we discuss using pseudospectra to substantiate the model in experimental contexts and establish bio-variability via data-driven methods. This work is the first to utilize pseudospectra to explore the HPA axis.

Limits and Powers of Koopman Learning

Dynamical systems provide a comprehensive way to study complex and changing behaviors across various sciences. Many modern systems are too complicated to analyze directly or we do not have access to models, driving significant interest in learning methods. Koopman operators have emerged as a dominant approach because they allow the study of nonlinear dynamics using linear techniques by solving an infinite-dimensional spectral problem. However, current algorithms face challenges such as lack of convergence, hindering practical progress. This paper addresses a fundamental open question: \textit{When can we robustly learn the spectral properties of Koopman operators from trajectory data of dynamical systems, and when can we not?} Understanding these boundaries is crucial for analysis, applications, and designing algorithms. We establish a foundational approach that combines computational analysis and ergodic theory, revealing the first fundamental barriers -- universal for any algorithm -- associated with system geometry and complexity, regardless of data quality and quantity. For instance, we demonstrate well-behaved smooth dynamical systems on tori where non-trivial eigenfunctions of the Koopman operator cannot be determined by any sequence of (even randomized) algorithms, even with unlimited training data. Additionally, we identify when learning is possible and introduce optimal algorithms with verification that overcome issues in standard methods. These results pave the way for a sharp classification theory of data-driven dynamical systems based on how many limits are needed to solve a problem. These limits characterize all previous methods, presenting a unified view. Our framework systematically determines when and how Koopman spectral properties can be learned.

Multiplicative Dynamic Mode Decomposition

Koopman operators are infinite-dimensional operators that linearize nonlinear dynamical systems, facilitating the study of their spectral properties and enabling the prediction of the time evolution of observable quantities. Recent methods have aimed to approximate Koopman operators while preserving key structures. However, approximating Koopman operators typically requires a dictionary of observables to capture the system's behavior in a finite-dimensional subspace. The selection of these functions is often heuristic, may result in the loss of spectral information, and can severely complicate structure preservation. This paper introduces Multiplicative Dynamic Mode Decomposition (MultDMD), which enforces the multiplicative structure inherent in the Koopman operator within its finite-dimensional approximation. Leveraging this multiplicative property, we guide the selection of observables and define a constrained optimization problem for the matrix approximation, which can be efficiently solved. MultDMD presents a structured approach to finite-dimensional approximations and can more accurately reflect the spectral properties of the Koopman operator. We elaborate on the theoretical framework of MultDMD, detailing its formulation, optimization strategy, and convergence properties. The efficacy of MultDMD is demonstrated through several examples, including the nonlinear pendulum, the Lorenz system, and fluid dynamics data, where we demonstrate its remarkable robustness to noise.

Rigged Dynamic Mode Decomposition: Data-Driven Generalized Eigenfunction Decompositions for Koopman Operators

We introduce the Rigged Dynamic Mode Decomposition (Rigged DMD) algorithm, which computes generalized eigenfunction decompositions of Koopman operators. By considering the evolution of observables, Koopman operators transform complex nonlinear dynamics into a linear framework suitable for spectral analysis. While powerful, traditional Dynamic Mode Decomposition (DMD) techniques often struggle with continuous spectra. Rigged DMD addresses these challenges with a data-driven methodology that approximates the Koopman operator's resolvent and its generalized eigenfunctions using snapshot data from the system's evolution. At its core, Rigged DMD builds wave-packet approximations for generalized Koopman eigenfunctions and modes by integrating Measure-Preserving Extended Dynamic Mode Decomposition with high-order kernels for smoothing. This provides a robust decomposition encompassing both discrete and continuous spectral elements. We derive explicit high-order convergence theorems for generalized eigenfunctions and spectral measures. Additionally, we propose a novel framework for constructing rigged Hilbert spaces using time-delay embedding, significantly extending the algorithm's applicability. We provide examples, including systems with a Lebesgue spectrum, integrable Hamiltonian systems, the Lorenz system, and a high-Reynolds number lid-driven flow in a two-dimensional square cavity, demonstrating Rigged DMD's convergence, efficiency, and versatility. This work paves the way for future research and applications of decompositions with continuous spectra.

On the Convergence of Hermitian Dynamic Mode Decomposition

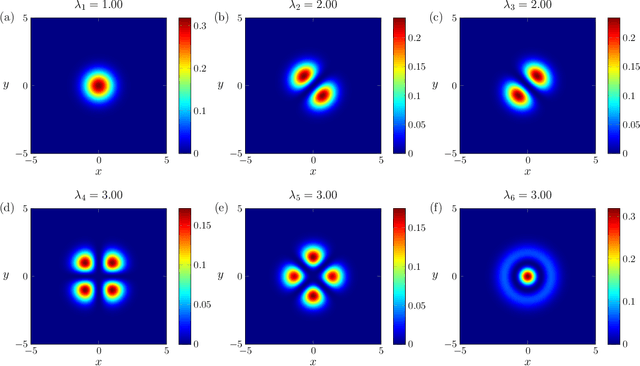
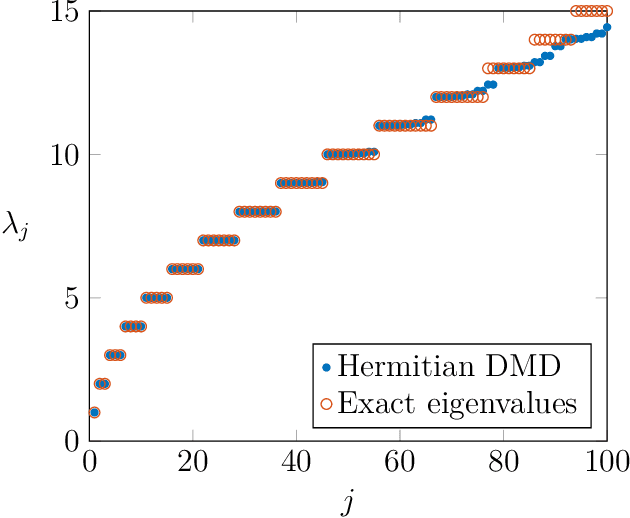
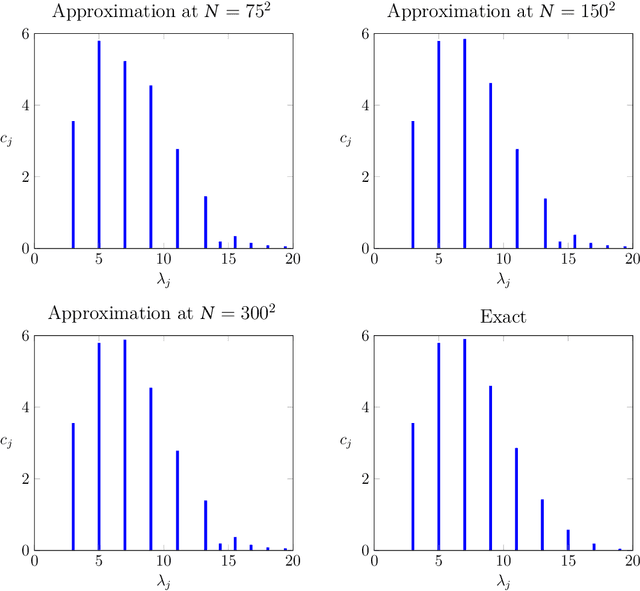
In this work, we study the convergence of Hermitian Dynamic Mode Decomposition (DMD) to the spectral properties of self-adjoint Koopman operators. Hermitian DMD is a data-driven method for approximating the Koopman operator associated with an unknown nonlinear dynamical system from discrete-time snapshots, while preserving the self-adjointness of the operator on its finite-dimensional approximations. We show that, under suitable conditions, the eigenvalues and eigenfunctions of HDMD converge to the spectral properties of the underlying Koopman operator. Along the way, we establish a general theorem on the convergence of spectral measures, and demonstrate our results numerically on the two-dimensional Schr\"odinger equation.

The Multiverse of Dynamic Mode Decomposition Algorithms

Dynamic Mode Decomposition (DMD) is a popular data-driven analysis technique used to decompose complex, nonlinear systems into a set of modes, revealing underlying patterns and dynamics through spectral analysis. This review presents a comprehensive and pedagogical examination of DMD, emphasizing the role of Koopman operators in transforming complex nonlinear dynamics into a linear framework. A distinctive feature of this review is its focus on the relationship between DMD and the spectral properties of Koopman operators, with particular emphasis on the theory and practice of DMD algorithms for spectral computations. We explore the diverse "multiverse" of DMD methods, categorized into three main areas: linear regression-based methods, Galerkin approximations, and structure-preserving techniques. Each category is studied for its unique contributions and challenges, providing a detailed overview of significant algorithms and their applications as outlined in Table 1. We include a MATLAB package with examples and applications to enhance the practical understanding of these methods. This review serves as both a practical guide and a theoretical reference for various DMD methods, accessible to both experts and newcomers, and enabling readers to delve into their areas of interest in the expansive field of DMD.

Beyond expectations: Residual Dynamic Mode Decomposition and Variance for Stochastic Dynamical Systems

Koopman operators linearize nonlinear dynamical systems, making their spectral information of crucial interest. Numerous algorithms have been developed to approximate these spectral properties, and Dynamic Mode Decomposition (DMD) stands out as the poster child of projection-based methods. Although the Koopman operator itself is linear, the fact that it acts in an infinite-dimensional space of observables poses challenges. These include spurious modes, essential spectra, and the verification of Koopman mode decompositions. While recent work has addressed these challenges for deterministic systems, there remains a notable gap in verified DMD methods for stochastic systems, where the Koopman operator measures the expectation of observables. We show that it is necessary to go beyond expectations to address these issues. By incorporating variance into the Koopman framework, we address these challenges. Through an additional DMD-type matrix, we approximate the sum of a squared residual and a variance term, each of which can be approximated individually using batched snapshot data. This allows verified computation of the spectral properties of stochastic Koopman operators, controlling the projection error. We also introduce the concept of variance-pseudospectra to gauge statistical coherency. Finally, we present a suite of convergence results for the spectral information of stochastic Koopman operators. Our study concludes with practical applications using both simulated and experimental data. In neural recordings from awake mice, we demonstrate how variance-pseudospectra can reveal physiologically significant information unavailable to standard expectation-based dynamical models.

Restarts subject to approximate sharpness: A parameter-free and optimal scheme for first-order methods

Sharpness is an almost generic assumption in continuous optimization that bounds the distance from minima by objective function suboptimality. It leads to the acceleration of first-order methods via restarts. However, sharpness involves problem-specific constants that are typically unknown, and previous restart schemes reduce convergence rates. Moreover, such schemes are challenging to apply in the presence of noise or approximate model classes (e.g., in compressive imaging or learning problems), and typically assume that the first-order method used produces feasible iterates. We consider the assumption of approximate sharpness, a generalization of sharpness that incorporates an unknown constant perturbation to the objective function error. This constant offers greater robustness (e.g., with respect to noise or relaxation of model classes) for finding approximate minimizers. By employing a new type of search over the unknown constants, we design a restart scheme that applies to general first-order methods and does not require the first-order method to produce feasible iterates. Our scheme maintains the same convergence rate as when assuming knowledge of the constants. The rates of convergence we obtain for various first-order methods either match the optimal rates or improve on previously established rates for a wide range of problems. We showcase our restart scheme on several examples and point to future applications and developments of our framework and theory.