Learning Lipschitz Operators with respect to Gaussian Measures with Near-Optimal Sample Complexity

Operator learning, the approximation of mappings between infinite-dimensional function spaces using ideas from machine learning, has gained increasing research attention in recent years. Approximate operators, learned from data, hold promise to serve as efficient surrogate models for problems in computational science and engineering, complementing traditional numerical methods. However, despite their empirical success, our understanding of the underpinning mathematical theory is in large part still incomplete. In this paper, we study the approximation of Lipschitz operators in expectation with respect to Gaussian measures. We prove higher Gaussian Sobolev regularity of Lipschitz operators and establish lower and upper bounds on the Hermite polynomial approximation error. We further consider the reconstruction of Lipschitz operators from $m$ arbitrary (adaptive) linear samples. A key finding is the tight characterization of the smallest achievable error for all possible (adaptive) sampling and reconstruction maps in terms of $m$. It is shown that Hermite polynomial approximation is an optimal recovery strategy, but we have the following curse of sample complexity: No method to approximate Lipschitz operators based on finitely many samples can achieve algebraic convergence rates in $m$. On the positive side, we prove that a sufficiently fast spectral decay of the covariance operator of the Gaussian measure guarantees convergence rates which are arbitrarily close to any algebraic rate in the large data limit $m \to \infty$. Finally, we focus on the recovery of Lipschitz operators from finitely many point samples. We consider Christoffel sampling and weighted least-squares approximation, and present an algorithm which provably achieves near-optimal sample complexity.

Optimal sampling for least-squares approximation

Least-squares approximation is one of the most important methods for recovering an unknown function from data. While in many applications the data is fixed, in many others there is substantial freedom to choose where to sample. In this paper, we review recent progress on optimal sampling for (weighted) least-squares approximation in arbitrary linear spaces. We introduce the Christoffel function as a key quantity in the analysis of (weighted) least-squares approximation from random samples, then show how it can be used to construct sampling strategies that possess near-optimal sample complexity: namely, the number of samples scales log-linearly in $n$, the dimension of the approximation space. We discuss a series of variations, extensions and further topics, and throughout highlight connections to approximation theory, machine learning, information-based complexity and numerical linear algebra. Finally, motivated by various contemporary applications, we consider a generalization of the classical setting where the samples need not be pointwise samples of a scalar-valued function, and the approximation space need not be linear. We show that even in this significantly more general setting suitable generalizations of the Christoffel function still determine the sample complexity. This provides a unified procedure for designing improved sampling strategies for general recovery problems. This article is largely self-contained, and intended to be accessible to nonspecialists.

On the consistent reasoning paradox of intelligence and optimal trust in AI: The power of 'I don't know'

We introduce the Consistent Reasoning Paradox (CRP). Consistent reasoning, which lies at the core of human intelligence, is the ability to handle tasks that are equivalent, yet described by different sentences ('Tell me the time!' and 'What is the time?'). The CRP asserts that consistent reasoning implies fallibility -- in particular, human-like intelligence in AI necessarily comes with human-like fallibility. Specifically, it states that there are problems, e.g. in basic arithmetic, where any AI that always answers and strives to mimic human intelligence by reasoning consistently will hallucinate (produce wrong, yet plausible answers) infinitely often. The paradox is that there exists a non-consistently reasoning AI (which therefore cannot be on the level of human intelligence) that will be correct on the same set of problems. The CRP also shows that detecting these hallucinations, even in a probabilistic sense, is strictly harder than solving the original problems, and that there are problems that an AI may answer correctly, but it cannot provide a correct logical explanation for how it arrived at the answer. Therefore, the CRP implies that any trustworthy AI (i.e., an AI that never answers incorrectly) that also reasons consistently must be able to say 'I don't know'. Moreover, this can only be done by implicitly computing a new concept that we introduce, termed the 'I don't know' function -- something currently lacking in modern AI. In view of these insights, the CRP also provides a glimpse into the behaviour of Artificial General Intelligence (AGI). An AGI cannot be 'almost sure', nor can it always explain itself, and therefore to be trustworthy it must be able to say 'I don't know'.

Optimal deep learning of holomorphic operators between Banach spaces

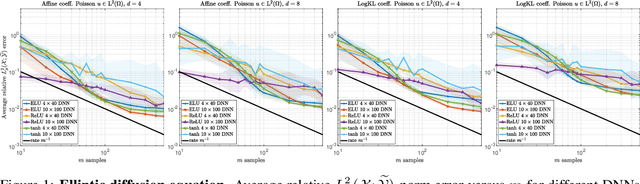
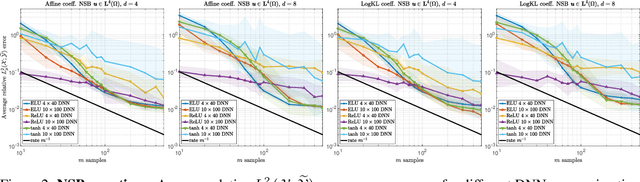
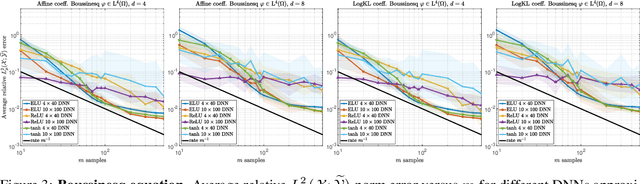
Operator learning problems arise in many key areas of scientific computing where Partial Differential Equations (PDEs) are used to model physical systems. In such scenarios, the operators map between Banach or Hilbert spaces. In this work, we tackle the problem of learning operators between Banach spaces, in contrast to the vast majority of past works considering only Hilbert spaces. We focus on learning holomorphic operators - an important class of problems with many applications. We combine arbitrary approximate encoders and decoders with standard feedforward Deep Neural Network (DNN) architectures - specifically, those with constant width exceeding the depth - under standard $\ell^2$-loss minimization. We first identify a family of DNNs such that the resulting Deep Learning (DL) procedure achieves optimal generalization bounds for such operators. For standard fully-connected architectures, we then show that there are uncountably many minimizers of the training problem that yield equivalent optimal performance. The DNN architectures we consider are `problem agnostic', with width and depth only depending on the amount of training data $m$ and not on regularity assumptions of the target operator. Next, we show that DL is optimal for this problem: no recovery procedure can surpass these generalization bounds up to log terms. Finally, we present numerical results demonstrating the practical performance on challenging problems including the parametric diffusion, Navier-Stokes-Brinkman and Boussinesq PDEs.

Learning smooth functions in high dimensions: from sparse polynomials to deep neural networks

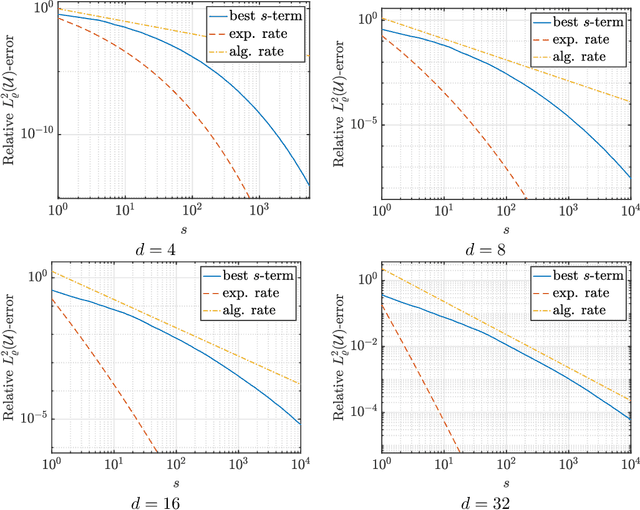
Learning approximations to smooth target functions of many variables from finite sets of pointwise samples is an important task in scientific computing and its many applications in computational science and engineering. Despite well over half a century of research on high-dimensional approximation, this remains a challenging problem. Yet, significant advances have been made in the last decade towards efficient methods for doing this, commencing with so-called sparse polynomial approximation methods and continuing most recently with methods based on Deep Neural Networks (DNNs). In tandem, there have been substantial advances in the relevant approximation theory and analysis of these techniques. In this work, we survey this recent progress. We describe the contemporary motivations for this problem, which stem from parametric models and computational uncertainty quantification; the relevant function classes, namely, classes of infinite-dimensional, Banach-valued, holomorphic functions; fundamental limits of learnability from finite data for these classes; and finally, sparse polynomial and DNN methods for efficiently learning such functions from finite data. For the latter, there is currently a significant gap between the approximation theory of DNNs and the practical performance of deep learning. Aiming to narrow this gap, we develop the topic of practical existence theory, which asserts the existence of dimension-independent DNN architectures and training strategies that achieve provably near-optimal generalization errors in terms of the amount of training data.

A unified framework for learning with nonlinear model classes from arbitrary linear samples

This work considers the fundamental problem of learning an unknown object from training data using a given model class. We introduce a unified framework that allows for objects in arbitrary Hilbert spaces, general types of (random) linear measurements as training data and general types of nonlinear model classes. We establish a series of learning guarantees for this framework. These guarantees provide explicit relations between the amount of training data and properties of the model class to ensure near-best generalization bounds. In doing so, we also introduce and develop the key notion of the variation of a model class with respect to a distribution of sampling operators. To exhibit the versatility of this framework, we show that it can accommodate many different types of well-known problems of interest. We present examples such as matrix sketching by random sampling, compressed sensing with isotropic vectors, active learning in regression and compressed sensing with generative models. In all cases, we show how known results become straightforward corollaries of our general learning guarantees. For compressed sensing with generative models, we also present a number of generalizations and improvements of recent results. In summary, our work not only introduces a unified way to study learning unknown objects from general types of data, but also establishes a series of general theoretical guarantees which consolidate and improve various known results.

CS4ML: A general framework for active learning with arbitrary data based on Christoffel functions

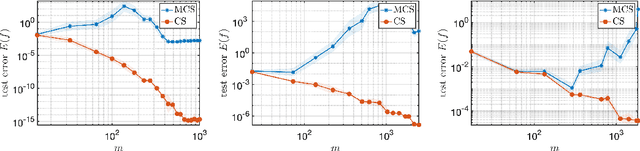
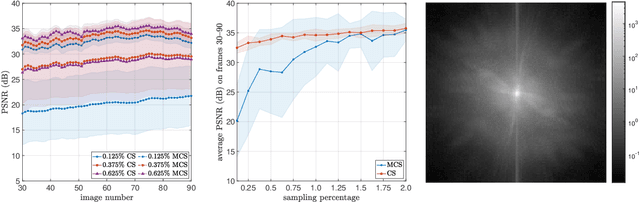
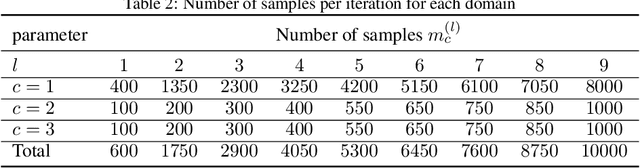
We introduce a general framework for active learning in regression problems. Our framework extends the standard setup by allowing for general types of data, rather than merely pointwise samples of the target function. This generalization covers many cases of practical interest, such as data acquired in transform domains (e.g., Fourier data), vector-valued data (e.g., gradient-augmented data), data acquired along continuous curves, and, multimodal data (i.e., combinations of different types of measurements). Our framework considers random sampling according to a finite number of sampling measures and arbitrary nonlinear approximation spaces (model classes). We introduce the concept of generalized Christoffel functions and show how these can be used to optimize the sampling measures. We prove that this leads to near-optimal sample complexity in various important cases. This paper focuses on applications in scientific computing, where active learning is often desirable, since it is usually expensive to generate data. We demonstrate the efficacy of our framework for gradient-augmented learning with polynomials, Magnetic Resonance Imaging (MRI) using generative models and adaptive sampling for solving PDEs using Physics-Informed Neural Networks (PINNs).

Restarts subject to approximate sharpness: A parameter-free and optimal scheme for first-order methods

Sharpness is an almost generic assumption in continuous optimization that bounds the distance from minima by objective function suboptimality. It leads to the acceleration of first-order methods via restarts. However, sharpness involves problem-specific constants that are typically unknown, and previous restart schemes reduce convergence rates. Moreover, such schemes are challenging to apply in the presence of noise or approximate model classes (e.g., in compressive imaging or learning problems), and typically assume that the first-order method used produces feasible iterates. We consider the assumption of approximate sharpness, a generalization of sharpness that incorporates an unknown constant perturbation to the objective function error. This constant offers greater robustness (e.g., with respect to noise or relaxation of model classes) for finding approximate minimizers. By employing a new type of search over the unknown constants, we design a restart scheme that applies to general first-order methods and does not require the first-order method to produce feasible iterates. Our scheme maintains the same convergence rate as when assuming knowledge of the constants. The rates of convergence we obtain for various first-order methods either match the optimal rates or improve on previously established rates for a wide range of problems. We showcase our restart scheme on several examples and point to future applications and developments of our framework and theory.

CAS4DL: Christoffel Adaptive Sampling for function approximation via Deep Learning

The problem of approximating smooth, multivariate functions from sample points arises in many applications in scientific computing, e.g., in computational Uncertainty Quantification (UQ) for science and engineering. In these applications, the target function may represent a desired quantity of interest of a parameterized Partial Differential Equation (PDE). Due to the large cost of solving such problems, where each sample is computed by solving a PDE, sample efficiency is a key concerning these applications. Recently, there has been increasing focus on the use of Deep Neural Networks (DNN) and Deep Learning (DL) for learning such functions from data. In this work, we propose an adaptive sampling strategy, CAS4DL (Christoffel Adaptive Sampling for Deep Learning) to increase the sample efficiency of DL for multivariate function approximation. Our novel approach is based on interpreting the second to last layer of a DNN as a dictionary of functions defined by the nodes on that layer. With this viewpoint, we then define an adaptive sampling strategy motivated by adaptive sampling schemes recently proposed for linear approximation schemes, wherein samples are drawn randomly with respect to the Christoffel function of the subspace spanned by this dictionary. We present numerical experiments comparing CAS4DL with standard Monte Carlo (MC) sampling. Our results demonstrate that CAS4DL often yields substantial savings in the number of samples required to achieve a given accuracy, particularly in the case of smooth activation functions, and it shows a better stability in comparison to MC. These results therefore are a promising step towards fully adapting DL towards scientific computing applications.

Is Monte Carlo a bad sampling strategy for learning smooth functions in high dimensions?

This paper concerns the approximation of smooth, high-dimensional functions from limited samples using polynomials. This task lies at the heart of many applications in computational science and engineering -- notably, those arising from parametric modelling and uncertainty quantification. It is common to use Monte Carlo (MC) sampling in such applications, so as not to succumb to the curse of dimensionality. However, it is well known this strategy is theoretically suboptimal. There are many polynomial spaces of dimension $n$ for which the sample complexity scales log-quadratically in $n$. This well-documented phenomenon has led to a concerted effort to design improved, in fact, near-optimal strategies, whose sample complexities scale log-linearly, or even linearly in $n$. Paradoxically, in this work we show that MC is actually a perfectly good strategy in high dimensions. We first document this phenomenon via several numerical examples. Next, we present a theoretical analysis that resolves this paradox for holomorphic functions of infinitely-many variables. We show that there is a least-squares scheme based on $m$ MC samples whose error decays algebraically fast in $m/\log(m)$, with a rate that is the same as that of the best $n$-term polynomial approximation. This result is non-constructive, since it assumes knowledge of a suitable polynomial space in which to perform the approximation. We next present a compressed sensing-based scheme that achieves the same rate, except for a larger polylogarithmic factor. This scheme is practical, and numerically it performs as well as or better than well-known adaptive least-squares schemes. Overall, our findings demonstrate that MC sampling is eminently suitable for smooth function approximation when the dimension is sufficiently high. Hence the benefits of improved sampling strategies are generically limited to lower-dimensional settings.