Optimal deep learning of holomorphic operators between Banach spaces

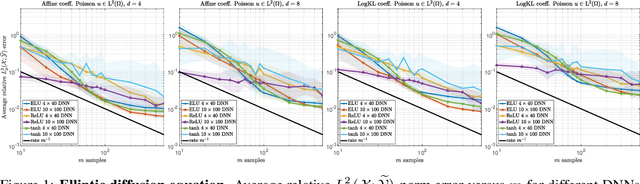
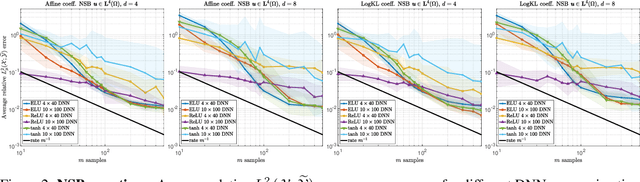
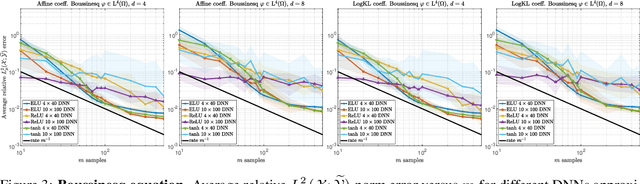
Operator learning problems arise in many key areas of scientific computing where Partial Differential Equations (PDEs) are used to model physical systems. In such scenarios, the operators map between Banach or Hilbert spaces. In this work, we tackle the problem of learning operators between Banach spaces, in contrast to the vast majority of past works considering only Hilbert spaces. We focus on learning holomorphic operators - an important class of problems with many applications. We combine arbitrary approximate encoders and decoders with standard feedforward Deep Neural Network (DNN) architectures - specifically, those with constant width exceeding the depth - under standard $\ell^2$-loss minimization. We first identify a family of DNNs such that the resulting Deep Learning (DL) procedure achieves optimal generalization bounds for such operators. For standard fully-connected architectures, we then show that there are uncountably many minimizers of the training problem that yield equivalent optimal performance. The DNN architectures we consider are `problem agnostic', with width and depth only depending on the amount of training data $m$ and not on regularity assumptions of the target operator. Next, we show that DL is optimal for this problem: no recovery procedure can surpass these generalization bounds up to log terms. Finally, we present numerical results demonstrating the practical performance on challenging problems including the parametric diffusion, Navier-Stokes-Brinkman and Boussinesq PDEs.

Physics-informed deep learning and compressive collocation for high-dimensional diffusion-reaction equations: practical existence theory and numerics

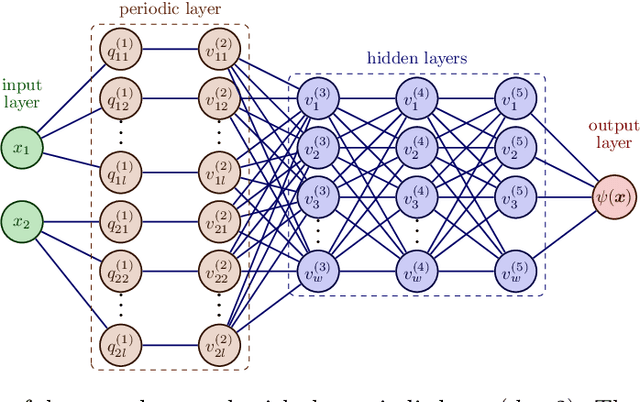
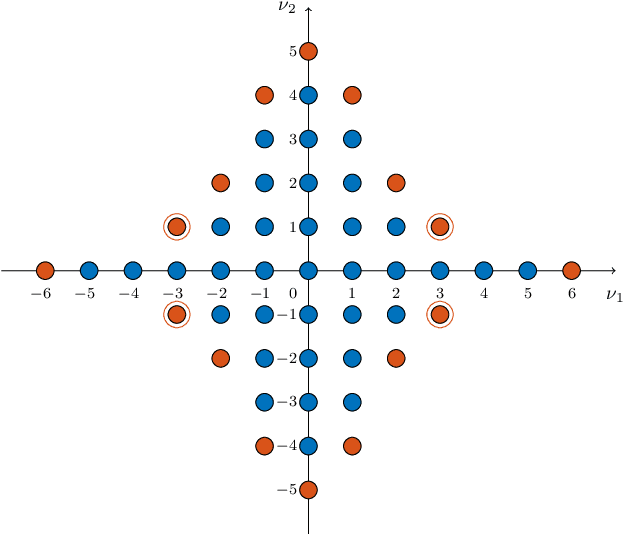
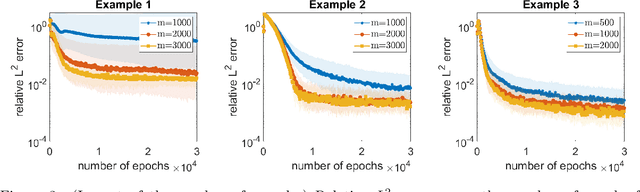
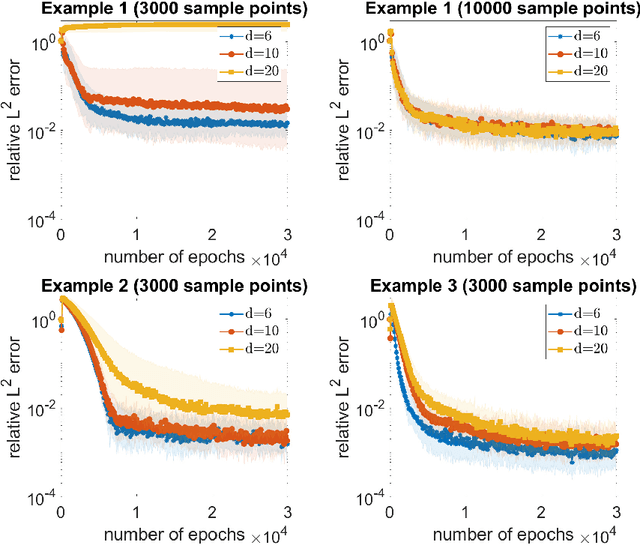
On the forefront of scientific computing, Deep Learning (DL), i.e., machine learning with Deep Neural Networks (DNNs), has emerged a powerful new tool for solving Partial Differential Equations (PDEs). It has been observed that DNNs are particularly well suited to weakening the effect of the curse of dimensionality, a term coined by Richard E. Bellman in the late `50s to describe challenges such as the exponential dependence of the sample complexity, i.e., the number of samples required to solve an approximation problem, on the dimension of the ambient space. However, although DNNs have been used to solve PDEs since the `90s, the literature underpinning their mathematical efficiency in terms of numerical analysis (i.e., stability, accuracy, and sample complexity), is only recently beginning to emerge. In this paper, we leverage recent advancements in function approximation using sparsity-based techniques and random sampling to develop and analyze an efficient high-dimensional PDE solver based on DL. We show, both theoretically and numerically, that it can compete with a novel stable and accurate compressive spectral collocation method. In particular, we demonstrate a new practical existence theorem, which establishes the existence of a class of trainable DNNs with suitable bounds on the network architecture and a sufficient condition on the sample complexity, with logarithmic or, at worst, linear scaling in dimension, such that the resulting networks stably and accurately approximate a diffusion-reaction PDE with high probability.

Learning smooth functions in high dimensions: from sparse polynomials to deep neural networks

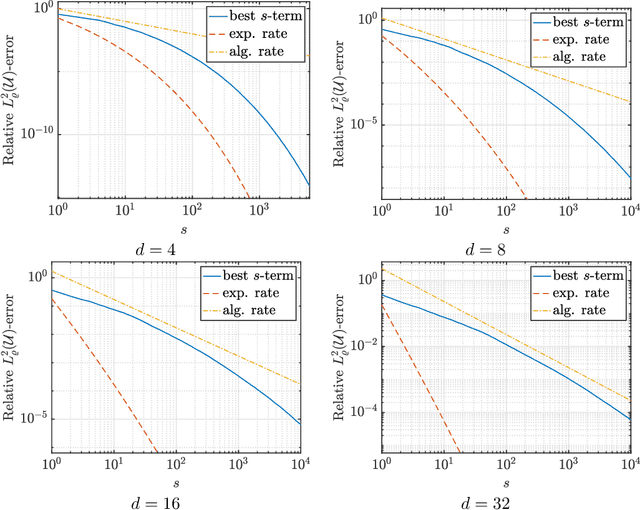
Learning approximations to smooth target functions of many variables from finite sets of pointwise samples is an important task in scientific computing and its many applications in computational science and engineering. Despite well over half a century of research on high-dimensional approximation, this remains a challenging problem. Yet, significant advances have been made in the last decade towards efficient methods for doing this, commencing with so-called sparse polynomial approximation methods and continuing most recently with methods based on Deep Neural Networks (DNNs). In tandem, there have been substantial advances in the relevant approximation theory and analysis of these techniques. In this work, we survey this recent progress. We describe the contemporary motivations for this problem, which stem from parametric models and computational uncertainty quantification; the relevant function classes, namely, classes of infinite-dimensional, Banach-valued, holomorphic functions; fundamental limits of learnability from finite data for these classes; and finally, sparse polynomial and DNN methods for efficiently learning such functions from finite data. For the latter, there is currently a significant gap between the approximation theory of DNNs and the practical performance of deep learning. Aiming to narrow this gap, we develop the topic of practical existence theory, which asserts the existence of dimension-independent DNN architectures and training strategies that achieve provably near-optimal generalization errors in terms of the amount of training data.

A unified framework for learning with nonlinear model classes from arbitrary linear samples

This work considers the fundamental problem of learning an unknown object from training data using a given model class. We introduce a unified framework that allows for objects in arbitrary Hilbert spaces, general types of (random) linear measurements as training data and general types of nonlinear model classes. We establish a series of learning guarantees for this framework. These guarantees provide explicit relations between the amount of training data and properties of the model class to ensure near-best generalization bounds. In doing so, we also introduce and develop the key notion of the variation of a model class with respect to a distribution of sampling operators. To exhibit the versatility of this framework, we show that it can accommodate many different types of well-known problems of interest. We present examples such as matrix sketching by random sampling, compressed sensing with isotropic vectors, active learning in regression and compressed sensing with generative models. In all cases, we show how known results become straightforward corollaries of our general learning guarantees. For compressed sensing with generative models, we also present a number of generalizations and improvements of recent results. In summary, our work not only introduces a unified way to study learning unknown objects from general types of data, but also establishes a series of general theoretical guarantees which consolidate and improve various known results.

CS4ML: A general framework for active learning with arbitrary data based on Christoffel functions

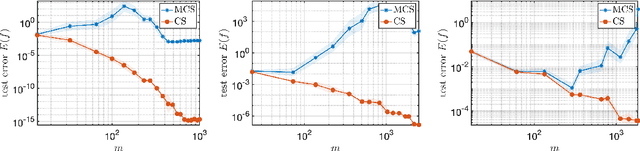
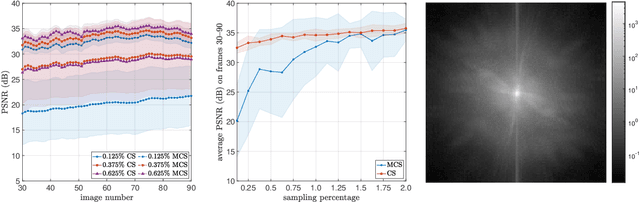
We introduce a general framework for active learning in regression problems. Our framework extends the standard setup by allowing for general types of data, rather than merely pointwise samples of the target function. This generalization covers many cases of practical interest, such as data acquired in transform domains (e.g., Fourier data), vector-valued data (e.g., gradient-augmented data), data acquired along continuous curves, and, multimodal data (i.e., combinations of different types of measurements). Our framework considers random sampling according to a finite number of sampling measures and arbitrary nonlinear approximation spaces (model classes). We introduce the concept of generalized Christoffel functions and show how these can be used to optimize the sampling measures. We prove that this leads to near-optimal sample complexity in various important cases. This paper focuses on applications in scientific computing, where active learning is often desirable, since it is usually expensive to generate data. We demonstrate the efficacy of our framework for gradient-augmented learning with polynomials, Magnetic Resonance Imaging (MRI) using generative models and adaptive sampling for solving PDEs using Physics-Informed Neural Networks (PINNs).

CAS4DL: Christoffel Adaptive Sampling for function approximation via Deep Learning

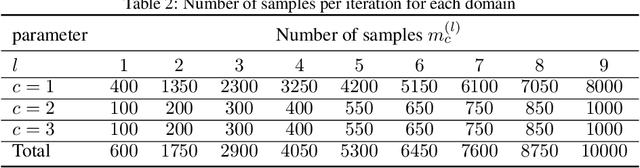
The problem of approximating smooth, multivariate functions from sample points arises in many applications in scientific computing, e.g., in computational Uncertainty Quantification (UQ) for science and engineering. In these applications, the target function may represent a desired quantity of interest of a parameterized Partial Differential Equation (PDE). Due to the large cost of solving such problems, where each sample is computed by solving a PDE, sample efficiency is a key concerning these applications. Recently, there has been increasing focus on the use of Deep Neural Networks (DNN) and Deep Learning (DL) for learning such functions from data. In this work, we propose an adaptive sampling strategy, CAS4DL (Christoffel Adaptive Sampling for Deep Learning) to increase the sample efficiency of DL for multivariate function approximation. Our novel approach is based on interpreting the second to last layer of a DNN as a dictionary of functions defined by the nodes on that layer. With this viewpoint, we then define an adaptive sampling strategy motivated by adaptive sampling schemes recently proposed for linear approximation schemes, wherein samples are drawn randomly with respect to the Christoffel function of the subspace spanned by this dictionary. We present numerical experiments comparing CAS4DL with standard Monte Carlo (MC) sampling. Our results demonstrate that CAS4DL often yields substantial savings in the number of samples required to achieve a given accuracy, particularly in the case of smooth activation functions, and it shows a better stability in comparison to MC. These results therefore are a promising step towards fully adapting DL towards scientific computing applications.

On efficient algorithms for computing near-best polynomial approximations to high-dimensional, Hilbert-valued functions from limited samples

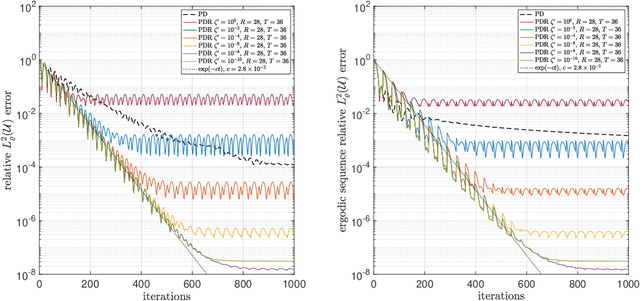
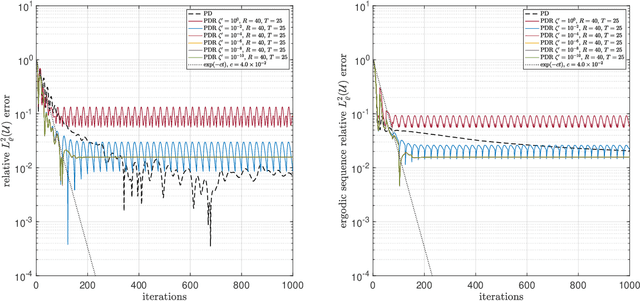
Sparse polynomial approximation has become indispensable for approximating smooth, high- or infinite-dimensional functions from limited samples. This is a key task in computational science and engineering, e.g., surrogate modelling in UQ where the function is the solution map of a parametric or stochastic PDE. Yet, sparse polynomial approximation lacks a complete theory. On the one hand, there is a well-developed theory of best $s$-term polynomial approximation, which asserts exponential or algebraic rates of convergence for holomorphic functions. On the other hand, there are increasingly mature methods such as (weighted) $\ell^1$-minimization for computing such approximations. While the sample complexity of these methods has been analyzed in detail, the matter of whether or not these methods achieve such rates is not well understood. Furthermore, these methods are not algorithms per se, since they involve exact minimizers of nonlinear optimization problems. This paper closes these gaps. Specifically, we pose and answer the following question: are there robust, efficient algorithms for computing approximations to finite- or infinite-dimensional, holomorphic and Hilbert-valued functions from limited samples that achieve best $s$-term rates? We answer this in the affirmative by introducing algorithms and theoretical guarantees that assert exponential or algebraic rates of convergence, along with robustness to sampling, algorithmic, and physical discretization errors. We tackle both scalar- and Hilbert-valued functions, this being particularly relevant to parametric and stochastic PDEs. Our work involves several significant developments of existing techniques, including a novel restarted primal-dual iteration for solving weighted $\ell^1$-minimization problems in Hilbert spaces. Our theory is supplemented by numerical experiments demonstrating the practical efficacy of these algorithms.

Deep Neural Networks Are Effective At Learning High-Dimensional Hilbert-Valued Functions From Limited Data

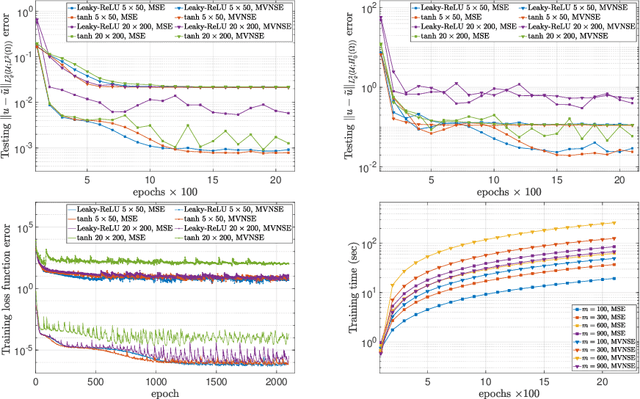
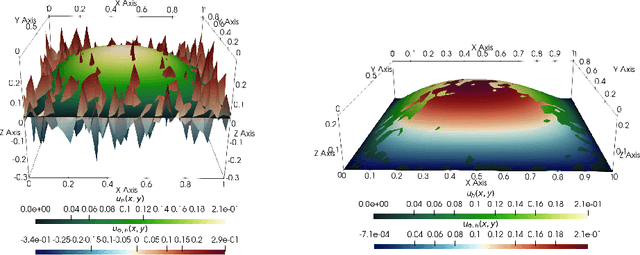
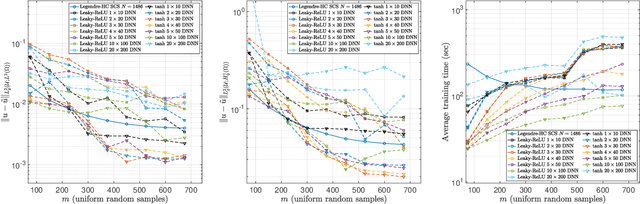
The accurate approximation of scalar-valued functions from sample points is a key task in mathematical modeling and computational science. Recently, machine learning techniques based on Deep Neural Networks (DNNs) have begun to emerge as promising tools for function approximation in scientific computing problems, with impressive results achieved on problems where the dimension of the underlying data or problem domain is large. In this work, we broaden this perspective by focusing on approximation of functions that are Hilbert-valued, i.e. they take values in a separable, but typically infinite-dimensional, Hilbert space. This problem arises in many science and engineering problems, in particular those involving the solution of parametric Partial Differential Equations (PDEs). Such problems are challenging for three reasons. First, pointwise samples are expensive to acquire. Second, the domain of the function is usually high dimensional, and third, the range lies in a Hilbert space. Our contributions are twofold. First, we present a novel result on DNN training for holomorphic functions with so-called hidden anisotropy. This result introduces a DNN training procedure and a full theoretical analysis with explicit guarantees on the error and sample complexity. This error bound is explicit in the three key errors occurred in the approximation procedure: best approximation error, measurement error and physical discretization error. Our result shows that there is a procedure for learning Hilbert-valued functions via DNNs that performs as well as current best-in-class schemes. Second, we provide preliminary numerical results illustrating the practical performance of DNNs on Hilbert-valued functions arising as solutions to parametric PDEs. We consider different parameters, modify the DNN architecture to achieve better and competitive results and compare these to current best-in-class schemes.

The gap between theory and practice in function approximation with deep neural networks

Deep learning (DL) is transforming whole industries as complicated decision-making processes are being automated by Deep Neural Networks (DNNs) trained on real-world data. Driven in part by a rapidly-expanding literature on DNN approximation theory showing that DNNs can approximate a rich variety of functions, these tools are increasingly being considered for problems in scientific computing. Yet, unlike more traditional algorithms in this field, relatively little is known about DNNs from the principles of numerical analysis, namely, stability, accuracy, computational efficiency and sample complexity. In this paper we introduce a computational framework for examining DNNs in practice, and use it to study their empirical performance with regard to these issues. We examine the performance of DNNs of different widths and depths on a variety of test functions in various dimensions, including smooth and piecewise smooth functions. We also compare DL against best-in-class methods for smooth function approximation based on compressed sensing. Our main conclusion is that there is a crucial gap between the approximation theory of DNNs and their practical performance, with trained DNNs performing relatively poorly on functions for which there are strong approximation results (e.g. smooth functions), yet performing well in comparison to best-in-class methods for other functions. Finally, we present a novel practical existence theorem, which asserts the existence of a DNN architecture and training procedure which offers the same performance as current best-in-class schemes. This result indicates the potential for practical DNN approximation, and the need for future research into practical architecture design and training strategies.