A unified framework for learning with nonlinear model classes from arbitrary linear samples

This work considers the fundamental problem of learning an unknown object from training data using a given model class. We introduce a unified framework that allows for objects in arbitrary Hilbert spaces, general types of (random) linear measurements as training data and general types of nonlinear model classes. We establish a series of learning guarantees for this framework. These guarantees provide explicit relations between the amount of training data and properties of the model class to ensure near-best generalization bounds. In doing so, we also introduce and develop the key notion of the variation of a model class with respect to a distribution of sampling operators. To exhibit the versatility of this framework, we show that it can accommodate many different types of well-known problems of interest. We present examples such as matrix sketching by random sampling, compressed sensing with isotropic vectors, active learning in regression and compressed sensing with generative models. In all cases, we show how known results become straightforward corollaries of our general learning guarantees. For compressed sensing with generative models, we also present a number of generalizations and improvements of recent results. In summary, our work not only introduces a unified way to study learning unknown objects from general types of data, but also establishes a series of general theoretical guarantees which consolidate and improve various known results.

CS4ML: A general framework for active learning with arbitrary data based on Christoffel functions

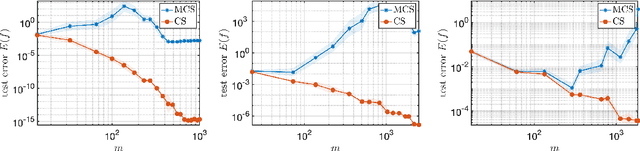
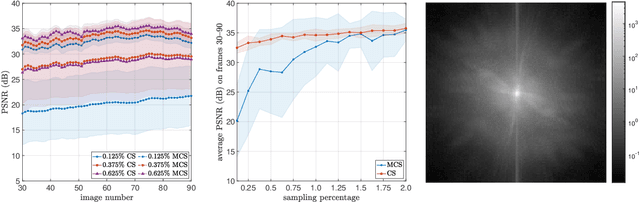
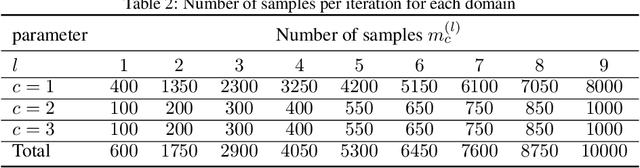
We introduce a general framework for active learning in regression problems. Our framework extends the standard setup by allowing for general types of data, rather than merely pointwise samples of the target function. This generalization covers many cases of practical interest, such as data acquired in transform domains (e.g., Fourier data), vector-valued data (e.g., gradient-augmented data), data acquired along continuous curves, and, multimodal data (i.e., combinations of different types of measurements). Our framework considers random sampling according to a finite number of sampling measures and arbitrary nonlinear approximation spaces (model classes). We introduce the concept of generalized Christoffel functions and show how these can be used to optimize the sampling measures. We prove that this leads to near-optimal sample complexity in various important cases. This paper focuses on applications in scientific computing, where active learning is often desirable, since it is usually expensive to generate data. We demonstrate the efficacy of our framework for gradient-augmented learning with polynomials, Magnetic Resonance Imaging (MRI) using generative models and adaptive sampling for solving PDEs using Physics-Informed Neural Networks (PINNs).

CAS4DL: Christoffel Adaptive Sampling for function approximation via Deep Learning

The problem of approximating smooth, multivariate functions from sample points arises in many applications in scientific computing, e.g., in computational Uncertainty Quantification (UQ) for science and engineering. In these applications, the target function may represent a desired quantity of interest of a parameterized Partial Differential Equation (PDE). Due to the large cost of solving such problems, where each sample is computed by solving a PDE, sample efficiency is a key concerning these applications. Recently, there has been increasing focus on the use of Deep Neural Networks (DNN) and Deep Learning (DL) for learning such functions from data. In this work, we propose an adaptive sampling strategy, CAS4DL (Christoffel Adaptive Sampling for Deep Learning) to increase the sample efficiency of DL for multivariate function approximation. Our novel approach is based on interpreting the second to last layer of a DNN as a dictionary of functions defined by the nodes on that layer. With this viewpoint, we then define an adaptive sampling strategy motivated by adaptive sampling schemes recently proposed for linear approximation schemes, wherein samples are drawn randomly with respect to the Christoffel function of the subspace spanned by this dictionary. We present numerical experiments comparing CAS4DL with standard Monte Carlo (MC) sampling. Our results demonstrate that CAS4DL often yields substantial savings in the number of samples required to achieve a given accuracy, particularly in the case of smooth activation functions, and it shows a better stability in comparison to MC. These results therefore are a promising step towards fully adapting DL towards scientific computing applications.