Deep Neural Networks Are Effective At Learning High-Dimensional Hilbert-Valued Functions From Limited Data
Paper and Code
Dec 11, 2020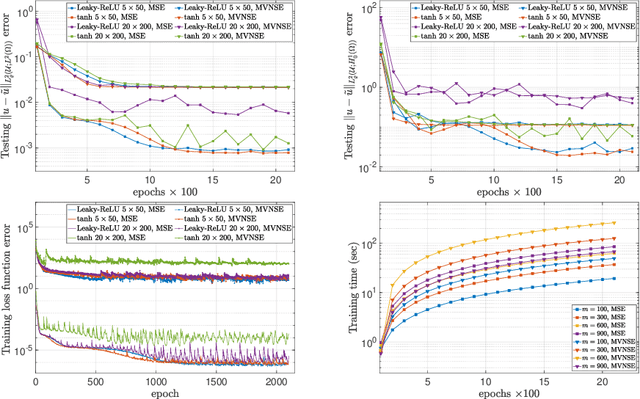
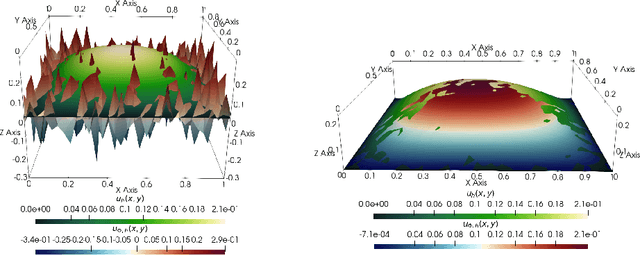
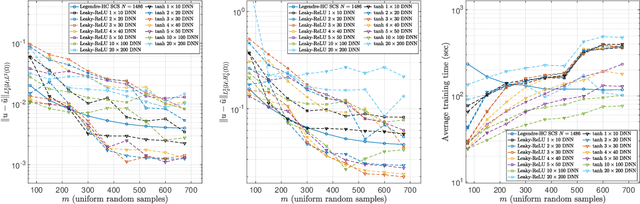
The accurate approximation of scalar-valued functions from sample points is a key task in mathematical modeling and computational science. Recently, machine learning techniques based on Deep Neural Networks (DNNs) have begun to emerge as promising tools for function approximation in scientific computing problems, with impressive results achieved on problems where the dimension of the underlying data or problem domain is large. In this work, we broaden this perspective by focusing on approximation of functions that are Hilbert-valued, i.e. they take values in a separable, but typically infinite-dimensional, Hilbert space. This problem arises in many science and engineering problems, in particular those involving the solution of parametric Partial Differential Equations (PDEs). Such problems are challenging for three reasons. First, pointwise samples are expensive to acquire. Second, the domain of the function is usually high dimensional, and third, the range lies in a Hilbert space. Our contributions are twofold. First, we present a novel result on DNN training for holomorphic functions with so-called hidden anisotropy. This result introduces a DNN training procedure and a full theoretical analysis with explicit guarantees on the error and sample complexity. This error bound is explicit in the three key errors occurred in the approximation procedure: best approximation error, measurement error and physical discretization error. Our result shows that there is a procedure for learning Hilbert-valued functions via DNNs that performs as well as current best-in-class schemes. Second, we provide preliminary numerical results illustrating the practical performance of DNNs on Hilbert-valued functions arising as solutions to parametric PDEs. We consider different parameters, modify the DNN architecture to achieve better and competitive results and compare these to current best-in-class schemes.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge