Optimal deep learning of holomorphic operators between Banach spaces
Paper and Code
Jun 20, 2024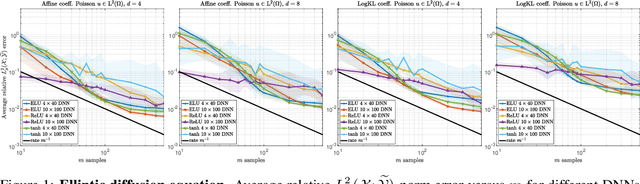
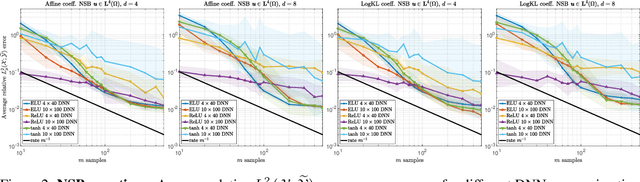
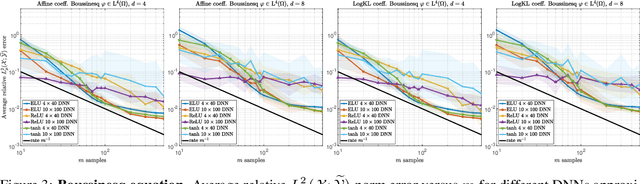
Operator learning problems arise in many key areas of scientific computing where Partial Differential Equations (PDEs) are used to model physical systems. In such scenarios, the operators map between Banach or Hilbert spaces. In this work, we tackle the problem of learning operators between Banach spaces, in contrast to the vast majority of past works considering only Hilbert spaces. We focus on learning holomorphic operators - an important class of problems with many applications. We combine arbitrary approximate encoders and decoders with standard feedforward Deep Neural Network (DNN) architectures - specifically, those with constant width exceeding the depth - under standard $\ell^2$-loss minimization. We first identify a family of DNNs such that the resulting Deep Learning (DL) procedure achieves optimal generalization bounds for such operators. For standard fully-connected architectures, we then show that there are uncountably many minimizers of the training problem that yield equivalent optimal performance. The DNN architectures we consider are `problem agnostic', with width and depth only depending on the amount of training data $m$ and not on regularity assumptions of the target operator. Next, we show that DL is optimal for this problem: no recovery procedure can surpass these generalization bounds up to log terms. Finally, we present numerical results demonstrating the practical performance on challenging problems including the parametric diffusion, Navier-Stokes-Brinkman and Boussinesq PDEs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge