Learning Lipschitz Operators with respect to Gaussian Measures with Near-Optimal Sample Complexity

Operator learning, the approximation of mappings between infinite-dimensional function spaces using ideas from machine learning, has gained increasing research attention in recent years. Approximate operators, learned from data, hold promise to serve as efficient surrogate models for problems in computational science and engineering, complementing traditional numerical methods. However, despite their empirical success, our understanding of the underpinning mathematical theory is in large part still incomplete. In this paper, we study the approximation of Lipschitz operators in expectation with respect to Gaussian measures. We prove higher Gaussian Sobolev regularity of Lipschitz operators and establish lower and upper bounds on the Hermite polynomial approximation error. We further consider the reconstruction of Lipschitz operators from $m$ arbitrary (adaptive) linear samples. A key finding is the tight characterization of the smallest achievable error for all possible (adaptive) sampling and reconstruction maps in terms of $m$. It is shown that Hermite polynomial approximation is an optimal recovery strategy, but we have the following curse of sample complexity: No method to approximate Lipschitz operators based on finitely many samples can achieve algebraic convergence rates in $m$. On the positive side, we prove that a sufficiently fast spectral decay of the covariance operator of the Gaussian measure guarantees convergence rates which are arbitrarily close to any algebraic rate in the large data limit $m \to \infty$. Finally, we focus on the recovery of Lipschitz operators from finitely many point samples. We consider Christoffel sampling and weighted least-squares approximation, and present an algorithm which provably achieves near-optimal sample complexity.

Convergence analysis of online algorithms for vector-valued kernel regression

We consider the problem of approximating the regression function from noisy vector-valued data by an online learning algorithm using an appropriate reproducing kernel Hilbert space (RKHS) as prior. In an online algorithm, i.i.d. samples become available one by one by a random process and are successively processed to build approximations to the regression function. We are interested in the asymptotic performance of such online approximation algorithms and show that the expected squared error in the RKHS norm can be bounded by $C^2 (m+1)^{-s/(2+s)}$, where $m$ is the current number of processed data, the parameter $0<s\leq 1$ expresses an additional smoothness assumption on the regression function and the constant $C$ depends on the variance of the input noise, the smoothness of the regression function and further parameters of the algorithm.

Deep Neural Networks and PIDE discretizations

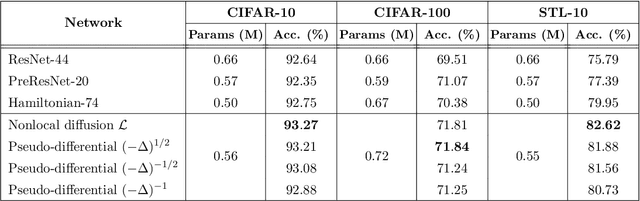
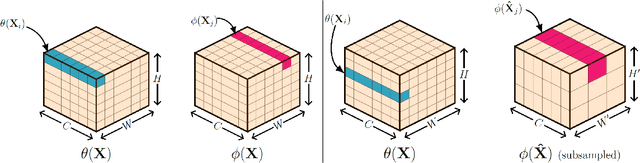
In this paper, we propose neural networks that tackle the problems of stability and field-of-view of a Convolutional Neural Network (CNN). As an alternative to increasing the network's depth or width to improve performance, we propose integral-based spatially nonlocal operators which are related to global weighted Laplacian, fractional Laplacian and inverse fractional Laplacian operators that arise in several problems in the physical sciences. The forward propagation of such networks is inspired by partial integro-differential equations (PIDEs). We test the effectiveness of the proposed neural architectures on benchmark image classification datasets and semantic segmentation tasks in autonomous driving. Moreover, we investigate the extra computational costs of these dense operators and the stability of forward propagation of the proposed neural networks.

Optimally rotated coordinate systems for adaptive least-squares regression on sparse grids

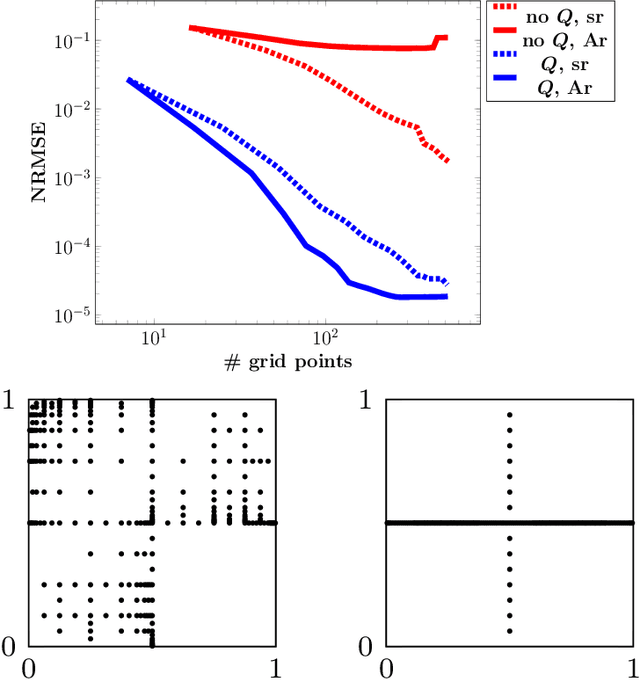
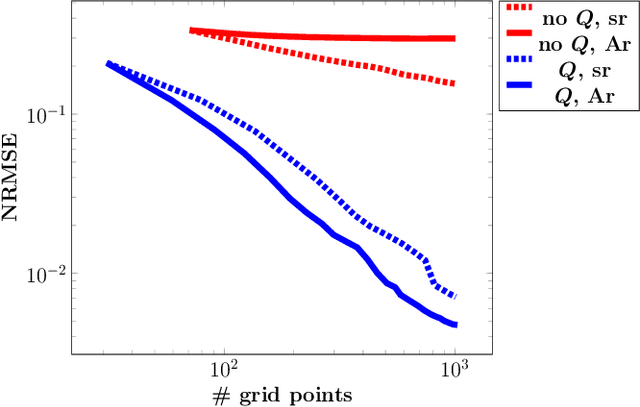
For low-dimensional data sets with a large amount of data points, standard kernel methods are usually not feasible for regression anymore. Besides simple linear models or involved heuristic deep learning models, grid-based discretizations of larger (kernel) model classes lead to algorithms, which naturally scale linearly in the amount of data points. For moderate-dimensional or high-dimensional regression tasks, these grid-based discretizations suffer from the curse of dimensionality. Here, sparse grid methods have proven to circumvent this problem to a large extent. In this context, space- and dimension-adaptive sparse grids, which can detect and exploit a given low effective dimensionality of nominally high-dimensional data, are particularly successful. They nevertheless rely on an axis-aligned structure of the solution and exhibit issues for data with predominantly skewed and rotated coordinates. In this paper we propose a preprocessing approach for these adaptive sparse grid algorithms that determines an optimized, problem-dependent coordinate system and, thus, reduces the effective dimensionality of a given data set in the ANOVA sense. We provide numerical examples on synthetic data as well as real-world data to show how an adaptive sparse grid least squares algorithm benefits from our preprocessing method.

A representer theorem for deep kernel learning

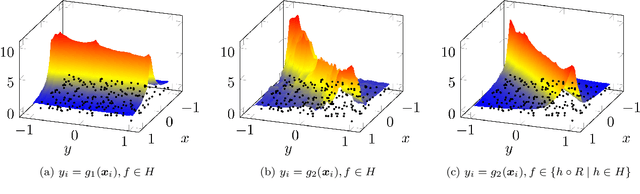
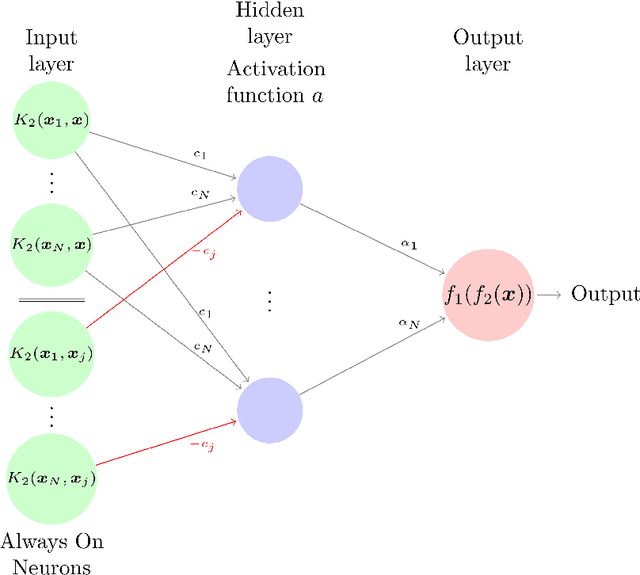
In this paper we provide a finite-sample and an infinite-sample representer theorem for the concatenation of (linear combinations of) kernel functions of reproducing kernel Hilbert spaces. These results serve as mathematical foundation for the analysis of machine learning algorithms based on compositions of functions. As a direct consequence in the finite-sample case, the corresponding infinite-dimensional minimization problems can be recast into (nonlinear) finite-dimensional minimization problems, which can be tackled with nonlinear optimization algorithms. Moreover, we show how concatenated machine learning problems can be reformulated as neural networks and how our representer theorem applies to a broad class of state-of-the-art deep learning methods.