Deep Neural Networks and PIDE discretizations
Paper and Code
Aug 05, 2021
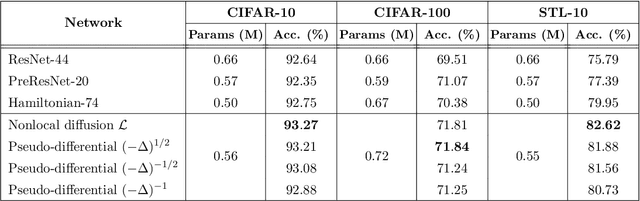
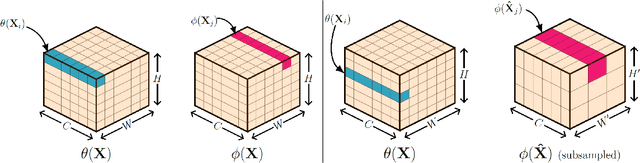

In this paper, we propose neural networks that tackle the problems of stability and field-of-view of a Convolutional Neural Network (CNN). As an alternative to increasing the network's depth or width to improve performance, we propose integral-based spatially nonlocal operators which are related to global weighted Laplacian, fractional Laplacian and inverse fractional Laplacian operators that arise in several problems in the physical sciences. The forward propagation of such networks is inspired by partial integro-differential equations (PIDEs). We test the effectiveness of the proposed neural architectures on benchmark image classification datasets and semantic segmentation tasks in autonomous driving. Moreover, we investigate the extra computational costs of these dense operators and the stability of forward propagation of the proposed neural networks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge