Deep Neural Networks and PIDE discretizations

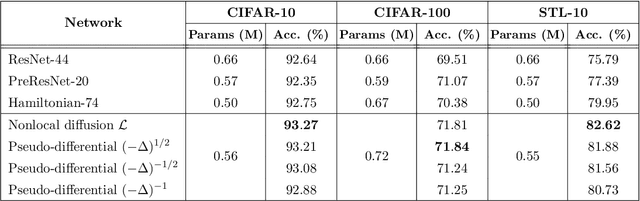
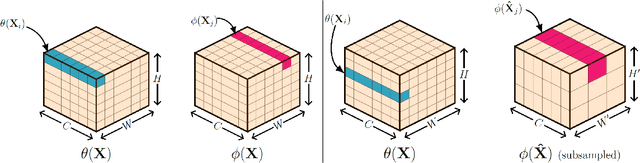
In this paper, we propose neural networks that tackle the problems of stability and field-of-view of a Convolutional Neural Network (CNN). As an alternative to increasing the network's depth or width to improve performance, we propose integral-based spatially nonlocal operators which are related to global weighted Laplacian, fractional Laplacian and inverse fractional Laplacian operators that arise in several problems in the physical sciences. The forward propagation of such networks is inspired by partial integro-differential equations (PIDEs). We test the effectiveness of the proposed neural architectures on benchmark image classification datasets and semantic segmentation tasks in autonomous driving. Moreover, we investigate the extra computational costs of these dense operators and the stability of forward propagation of the proposed neural networks.

Explainable Machine Learning for Scientific Insights and Discoveries

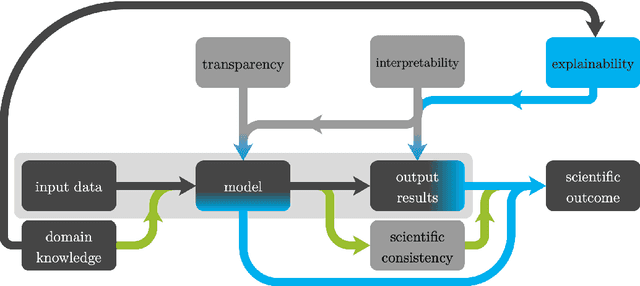
Machine learning methods have been remarkably successful for a wide range of application areas in the extraction of essential information from data. An exciting and relatively recent development is the uptake of machine learning in the natural sciences, where the major goal is to obtain novel scientific insights and discoveries from observational or simulated data. A prerequisite for obtaining a scientific outcome is domain knowledge, which is needed to gain explainability, but also to enhance scientific consistency. In this article we review explainable machine learning in view of applications in the natural sciences and discuss three core elements which we identified as relevant in this context: transparency, interpretability, and explainability. With respect to these core elements, we provide a survey of recent scientific works incorporating machine learning, and in particular to the way that explainable machine learning is used in their respective application areas.

Optimally rotated coordinate systems for adaptive least-squares regression on sparse grids

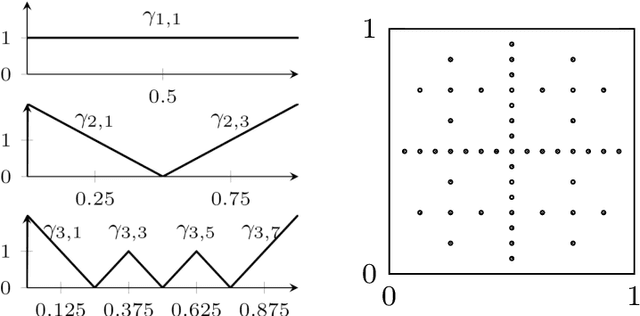
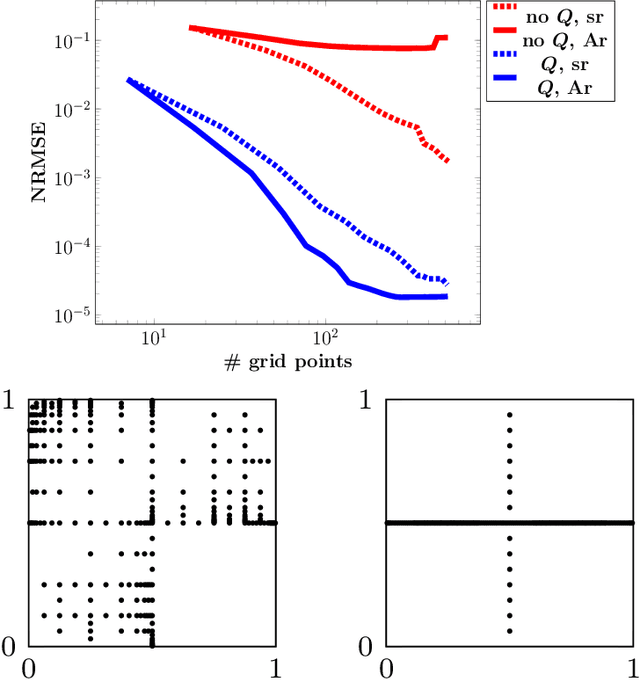
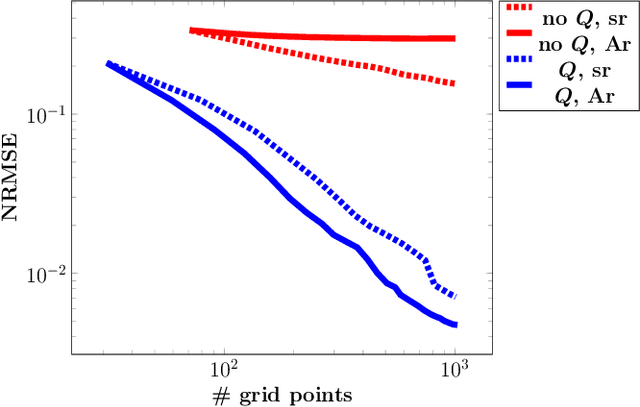
For low-dimensional data sets with a large amount of data points, standard kernel methods are usually not feasible for regression anymore. Besides simple linear models or involved heuristic deep learning models, grid-based discretizations of larger (kernel) model classes lead to algorithms, which naturally scale linearly in the amount of data points. For moderate-dimensional or high-dimensional regression tasks, these grid-based discretizations suffer from the curse of dimensionality. Here, sparse grid methods have proven to circumvent this problem to a large extent. In this context, space- and dimension-adaptive sparse grids, which can detect and exploit a given low effective dimensionality of nominally high-dimensional data, are particularly successful. They nevertheless rely on an axis-aligned structure of the solution and exhibit issues for data with predominantly skewed and rotated coordinates. In this paper we propose a preprocessing approach for these adaptive sparse grid algorithms that determines an optimized, problem-dependent coordinate system and, thus, reduces the effective dimensionality of a given data set in the ANOVA sense. We provide numerical examples on synthetic data as well as real-world data to show how an adaptive sparse grid least squares algorithm benefits from our preprocessing method.

A representer theorem for deep kernel learning

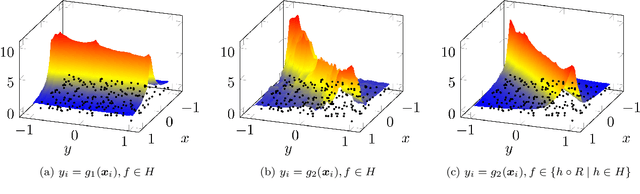
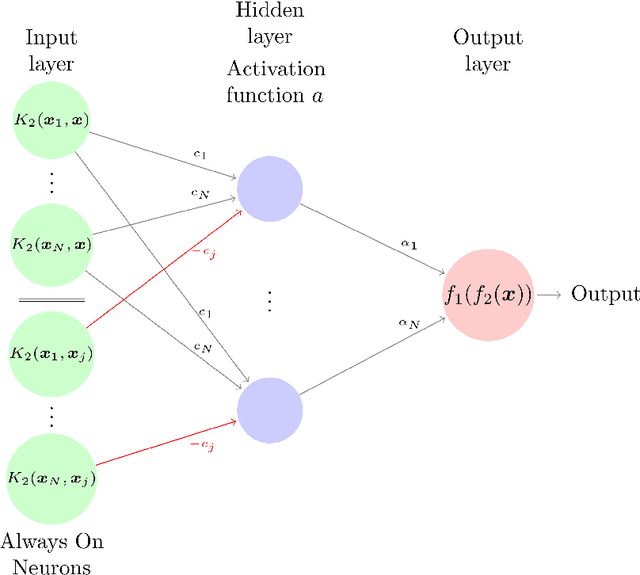
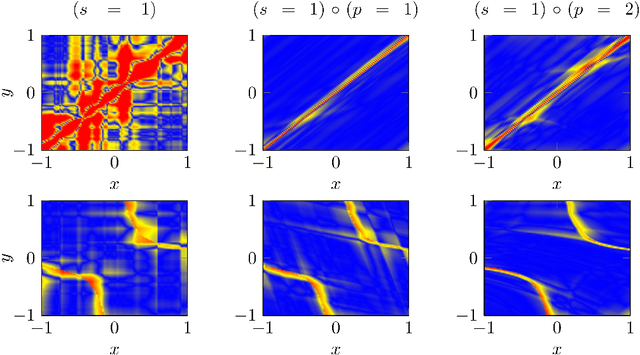
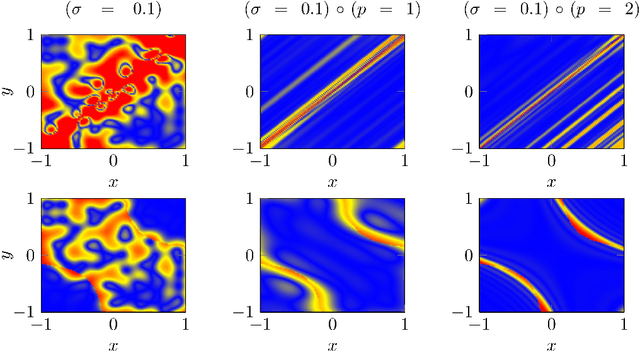
In this paper we provide a finite-sample and an infinite-sample representer theorem for the concatenation of (linear combinations of) kernel functions of reproducing kernel Hilbert spaces. These results serve as mathematical foundation for the analysis of machine learning algorithms based on compositions of functions. As a direct consequence in the finite-sample case, the corresponding infinite-dimensional minimization problems can be recast into (nonlinear) finite-dimensional minimization problems, which can be tackled with nonlinear optimization algorithms. Moreover, we show how concatenated machine learning problems can be reformulated as neural networks and how our representer theorem applies to a broad class of state-of-the-art deep learning methods.