Jens Oettershagen
Optimally rotated coordinate systems for adaptive least-squares regression on sparse grids
Oct 15, 2018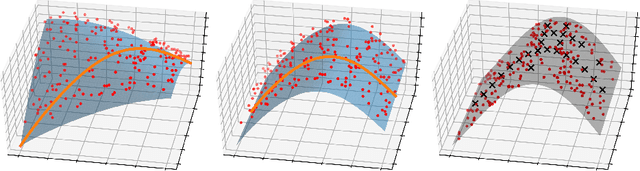
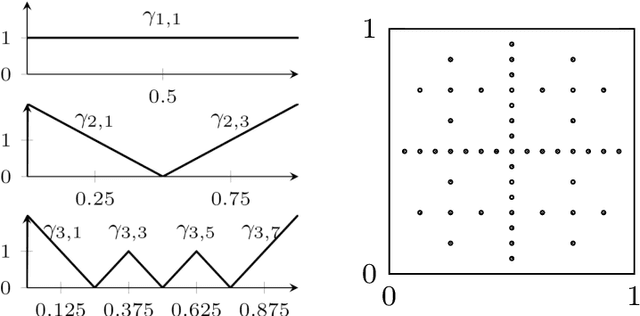
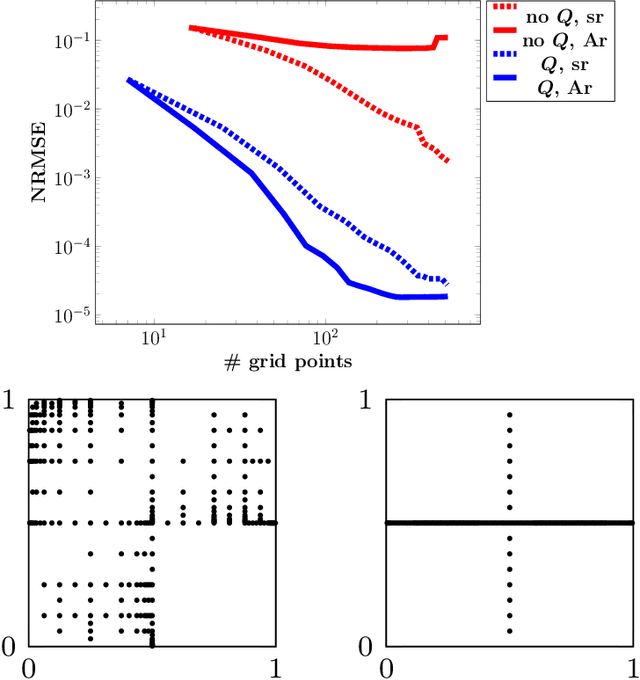
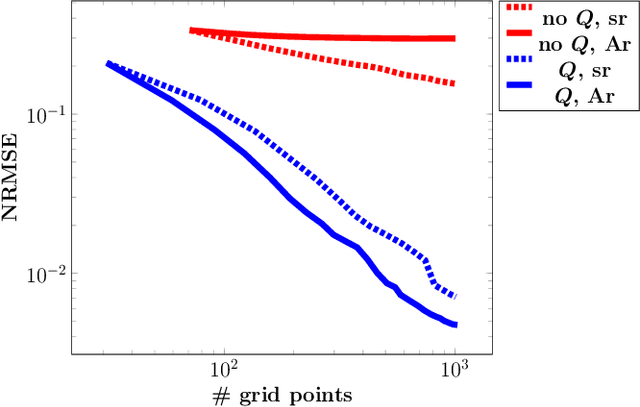
Abstract:For low-dimensional data sets with a large amount of data points, standard kernel methods are usually not feasible for regression anymore. Besides simple linear models or involved heuristic deep learning models, grid-based discretizations of larger (kernel) model classes lead to algorithms, which naturally scale linearly in the amount of data points. For moderate-dimensional or high-dimensional regression tasks, these grid-based discretizations suffer from the curse of dimensionality. Here, sparse grid methods have proven to circumvent this problem to a large extent. In this context, space- and dimension-adaptive sparse grids, which can detect and exploit a given low effective dimensionality of nominally high-dimensional data, are particularly successful. They nevertheless rely on an axis-aligned structure of the solution and exhibit issues for data with predominantly skewed and rotated coordinates. In this paper we propose a preprocessing approach for these adaptive sparse grid algorithms that determines an optimized, problem-dependent coordinate system and, thus, reduces the effective dimensionality of a given data set in the ANOVA sense. We provide numerical examples on synthetic data as well as real-world data to show how an adaptive sparse grid least squares algorithm benefits from our preprocessing method.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge