Restarts subject to approximate sharpness: A parameter-free and optimal scheme for first-order methods

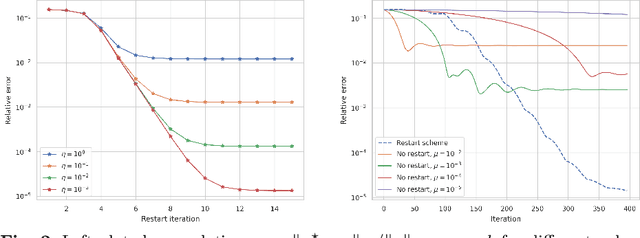
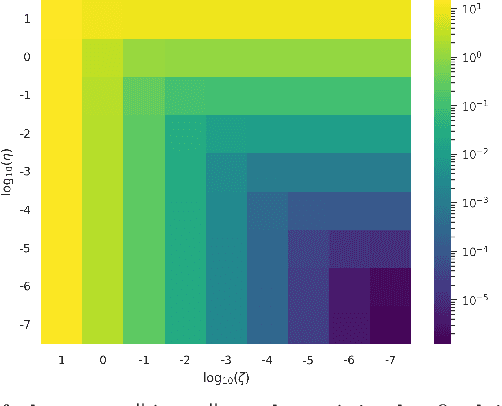
Sharpness is an almost generic assumption in continuous optimization that bounds the distance from minima by objective function suboptimality. It leads to the acceleration of first-order methods via restarts. However, sharpness involves problem-specific constants that are typically unknown, and previous restart schemes reduce convergence rates. Moreover, such schemes are challenging to apply in the presence of noise or approximate model classes (e.g., in compressive imaging or learning problems), and typically assume that the first-order method used produces feasible iterates. We consider the assumption of approximate sharpness, a generalization of sharpness that incorporates an unknown constant perturbation to the objective function error. This constant offers greater robustness (e.g., with respect to noise or relaxation of model classes) for finding approximate minimizers. By employing a new type of search over the unknown constants, we design a restart scheme that applies to general first-order methods and does not require the first-order method to produce feasible iterates. Our scheme maintains the same convergence rate as when assuming knowledge of the constants. The rates of convergence we obtain for various first-order methods either match the optimal rates or improve on previously established rates for a wide range of problems. We showcase our restart scheme on several examples and point to future applications and developments of our framework and theory.

Stable, accurate and efficient deep neural networks for inverse problems with analysis-sparse models

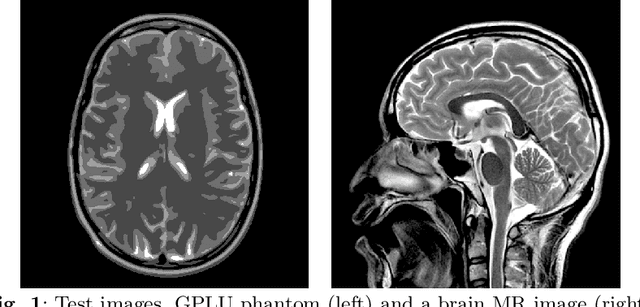
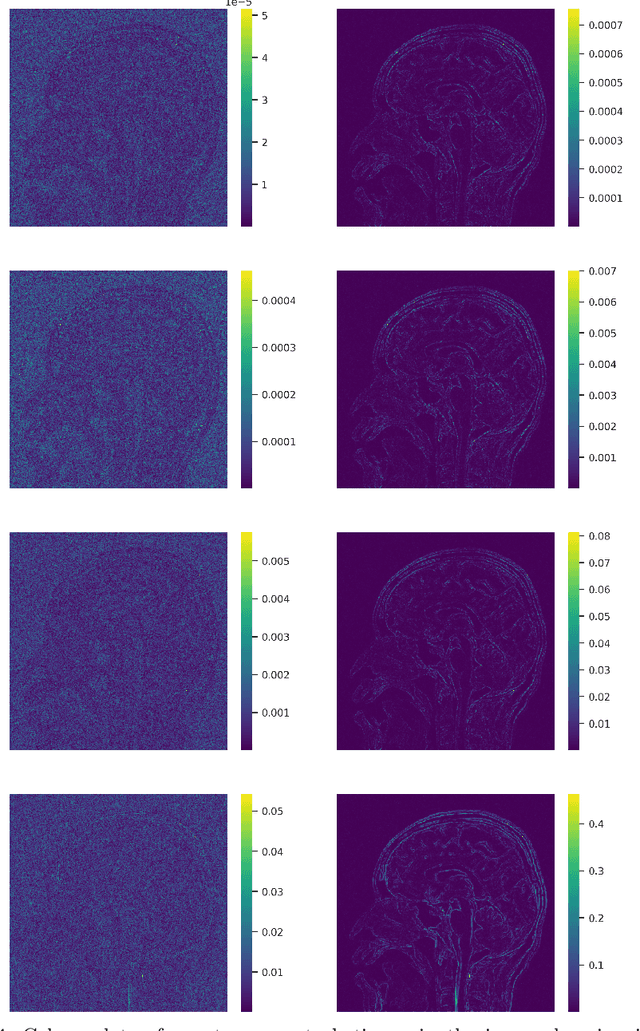
Solving inverse problems is a fundamental component of science, engineering and mathematics. With the advent of deep learning, deep neural networks have significant potential to outperform existing state-of-the-art, model-based methods for solving inverse problems. However, it is known that current data-driven approaches face several key issues, notably instabilities and hallucinations, with potential impact in critical tasks such as medical imaging. This raises the key question of whether or not one can construct stable and accurate deep neural networks for inverse problems. In this work, we present a novel construction of an accurate, stable and efficient neural network for inverse problems with general analysis-sparse models. To construct the network, we unroll NESTA, an accelerated first-order method for convex optimization. Combined with a compressed sensing analysis, we prove accuracy and stability. Finally, a restart scheme is employed to enable exponential decay of the required network depth, yielding a shallower, and consequently more efficient, network. We showcase this approach in the case of Fourier imaging, and verify its stability and performance via a series of numerical experiments. The key impact of this work is to provide theoretical guarantees for computing and developing stable neural networks in practice.