Stable, accurate and efficient deep neural networks for inverse problems with analysis-sparse models

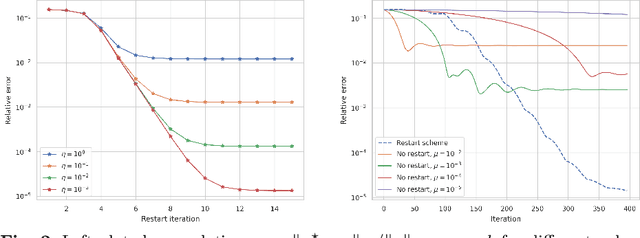
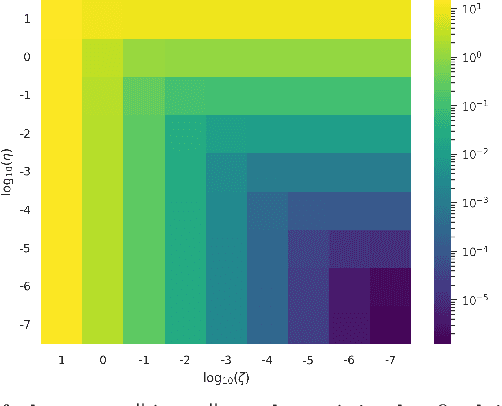
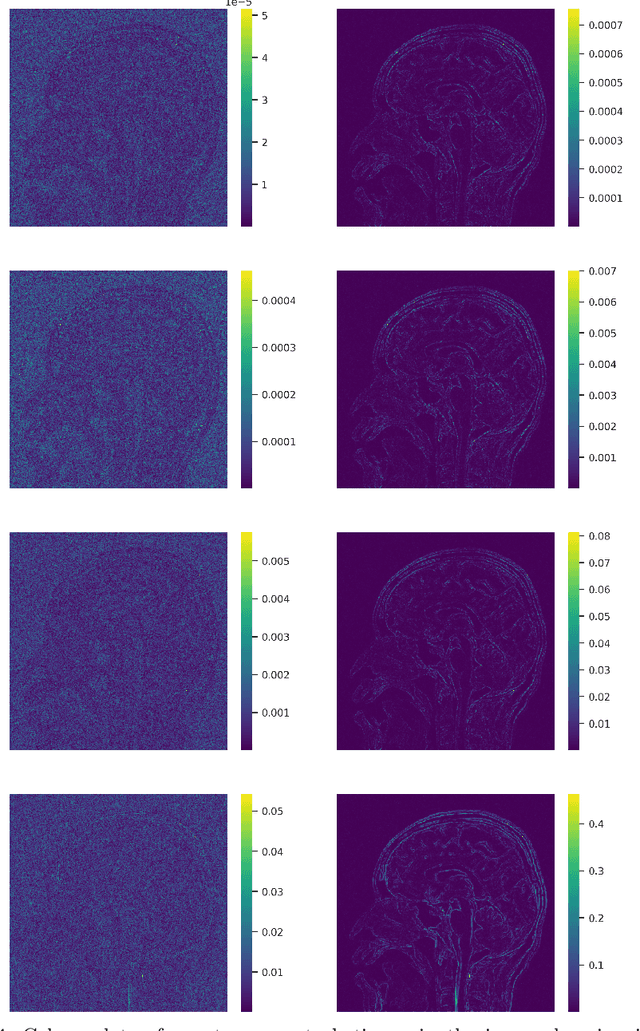
Solving inverse problems is a fundamental component of science, engineering and mathematics. With the advent of deep learning, deep neural networks have significant potential to outperform existing state-of-the-art, model-based methods for solving inverse problems. However, it is known that current data-driven approaches face several key issues, notably instabilities and hallucinations, with potential impact in critical tasks such as medical imaging. This raises the key question of whether or not one can construct stable and accurate deep neural networks for inverse problems. In this work, we present a novel construction of an accurate, stable and efficient neural network for inverse problems with general analysis-sparse models. To construct the network, we unroll NESTA, an accelerated first-order method for convex optimization. Combined with a compressed sensing analysis, we prove accuracy and stability. Finally, a restart scheme is employed to enable exponential decay of the required network depth, yielding a shallower, and consequently more efficient, network. We showcase this approach in the case of Fourier imaging, and verify its stability and performance via a series of numerical experiments. The key impact of this work is to provide theoretical guarantees for computing and developing stable neural networks in practice.