Koopman-driven grip force prediction through EMG sensing

Loss of hand function due to conditions like stroke or multiple sclerosis significantly impacts daily activities. Robotic rehabilitation provides tools to restore hand function, while novel methods based on surface electromyography (sEMG) enable the adaptation of the device's force output according to the user's condition, thereby improving rehabilitation outcomes. This study aims to achieve accurate force estimations during medium wrap grasps using a single sEMG sensor pair, thereby addressing the challenge of escalating sensor requirements for precise predictions. We conducted sEMG measurements on 13 subjects at two forearm positions, validating results with a hand dynamometer. We established flexible signal-processing steps, yielding high peak cross-correlations between the processed sEMG signal (representing meaningful muscle activity) and grip force. Influential parameters were subsequently identified through sensitivity analysis. Leveraging a novel data-driven Koopman operator theory-based approach and problem-specific data lifting techniques, we devised a methodology for the estimation and short-term prediction of grip force from processed sEMG signals. A weighted mean absolute percentage error (wMAPE) of approx. 5.5% was achieved for the estimated grip force, whereas predictions with a 0.5-second prediction horizon resulted in a wMAPE of approx. 17.9%. The methodology proved robust regarding precise electrode positioning, as the effect of sensing position on error metrics was non-significant. The algorithm executes exceptionally fast, processing, estimating, and predicting a 0.5-second sEMG signal batch in just approx. 30 ms, facilitating real-time implementation.

Limits and Powers of Koopman Learning

Dynamical systems provide a comprehensive way to study complex and changing behaviors across various sciences. Many modern systems are too complicated to analyze directly or we do not have access to models, driving significant interest in learning methods. Koopman operators have emerged as a dominant approach because they allow the study of nonlinear dynamics using linear techniques by solving an infinite-dimensional spectral problem. However, current algorithms face challenges such as lack of convergence, hindering practical progress. This paper addresses a fundamental open question: \textit{When can we robustly learn the spectral properties of Koopman operators from trajectory data of dynamical systems, and when can we not?} Understanding these boundaries is crucial for analysis, applications, and designing algorithms. We establish a foundational approach that combines computational analysis and ergodic theory, revealing the first fundamental barriers -- universal for any algorithm -- associated with system geometry and complexity, regardless of data quality and quantity. For instance, we demonstrate well-behaved smooth dynamical systems on tori where non-trivial eigenfunctions of the Koopman operator cannot be determined by any sequence of (even randomized) algorithms, even with unlimited training data. Additionally, we identify when learning is possible and introduce optimal algorithms with verification that overcome issues in standard methods. These results pave the way for a sharp classification theory of data-driven dynamical systems based on how many limits are needed to solve a problem. These limits characterize all previous methods, presenting a unified view. Our framework systematically determines when and how Koopman spectral properties can be learned.

Koopman Learning with Episodic Memory

Koopman operator theory, a data-driven dynamical systems framework, has found significant success in learning models from complex, real-world data sets, enabling state-of-the-art prediction and control. The greater interpretability and lower computational costs of these models, compared to traditional machine learning methodologies, make Koopman learning an especially appealing approach. Despite this, little work has been performed on endowing Koopman learning with the ability to learn from its own mistakes. To address this, we equip Koopman methods - developed for predicting non-stationary time-series - with an episodic memory mechanism, enabling global recall of (or attention to) periods in time where similar dynamics previously occurred. We find that a basic implementation of Koopman learning with episodic memory leads to significant improvements in prediction on synthetic and real-world data. Our framework has considerable potential for expansion, allowing for future advances, and opens exciting new directions for Koopman learning.

On Equivalent Optimization of Machine Learning Methods

At the core of many machine learning methods resides an iterative optimization algorithm for their training. Such optimization algorithms often come with a plethora of choices regarding their implementation. In the case of deep neural networks, choices of optimizer, learning rate, batch size, etc. must be made. Despite the fundamental way in which these choices impact the training of deep neural networks, there exists no general method for identifying when they lead to equivalent, or non-equivalent, optimization trajectories. By viewing iterative optimization as a discrete-time dynamical system, we are able to leverage Koopman operator theory, where it is known that conjugate dynamics can have identical spectral objects. We find highly overlapping Koopman spectra associated with the application of online mirror and gradient descent to specific problems, illustrating that such a data-driven approach can corroborate the recently discovered analytical equivalence between the two optimizers. We extend our analysis to feedforward, fully connected neural networks, providing the first general characterization of when choices of learning rate, batch size, layer width, data set, and activation function lead to equivalent, and non-equivalent, evolution of network parameters during training. Among our main results, we find that learning rate to batch size ratio, layer width, nature of data set (handwritten vs. synthetic), and activation function affect the nature of conjugacy. Our data-driven approach is general and can be utilized broadly to compare the optimization of machine learning methods.

Mean Subtraction and Mode Selection in Dynamic Mode Decomposition

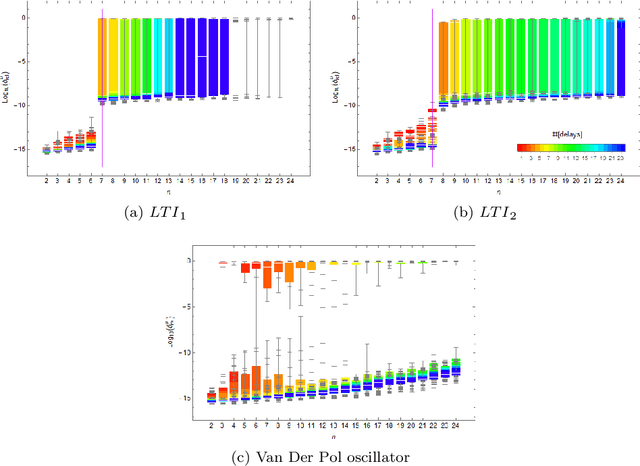
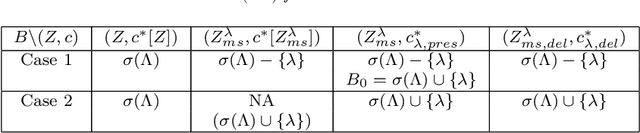
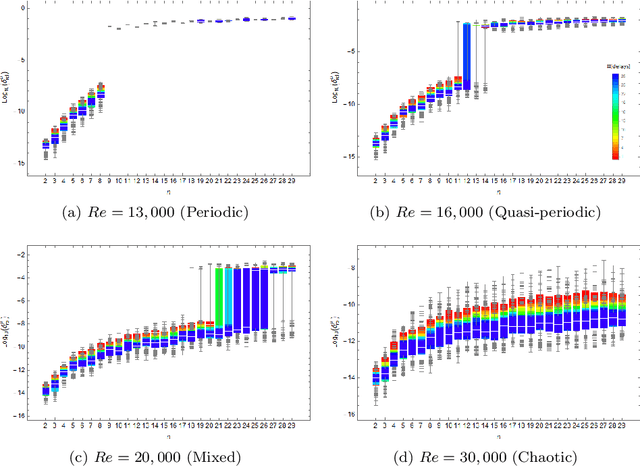
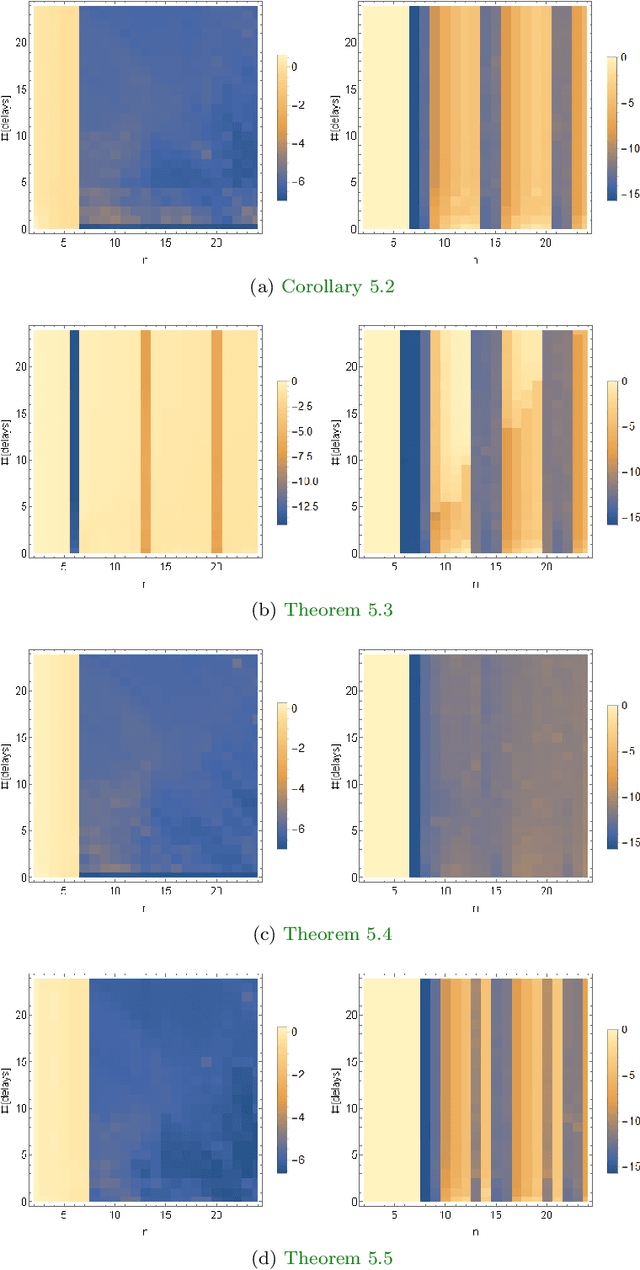
Koopman mode analysis has provided a framework for analysis of nonlinear phenomena across a plethora of fields. Its numerical implementation via Dynamic Mode Decomposition (DMD) has been extensively deployed and improved upon over the last decade. We address the problems of mean subtraction and DMD mode selection in the context of finite dimensional Koopman invariant subspaces. Preprocessing of data by subtraction of the temporal mean of a time series has been a point of contention in companion matrix-based DMD. This stems from the potential of said preprocessing to render DMD equivalent to temporal DFT. We prove that this equivalence is impossible when the order of the DMD-based representation of the dynamics exceeds the dimension of the system. Moreover, this parity of DMD and DFT is mostly indicative of an inadequacy of data, in the sense that the number of snapshots taken is not enough to represent the true dynamics of the system. We then vindicate the practice of pruning DMD eigenvalues based on the norm of the respective modes. Once a minimum number of time delays has been taken, DMD eigenvalues corresponding to DMD modes with low norm are shown to be spurious, and hence must be discarded. When dealing with mean-subtracted data, the above criterion for detecting synthetic eigenvalues can be applied after additional pre-processing. This takes the form of an eigenvalue constraint on Companion DMD, or yet another time delay.

Predicting the Critical Number of Layers for Hierarchical Support Vector Regression

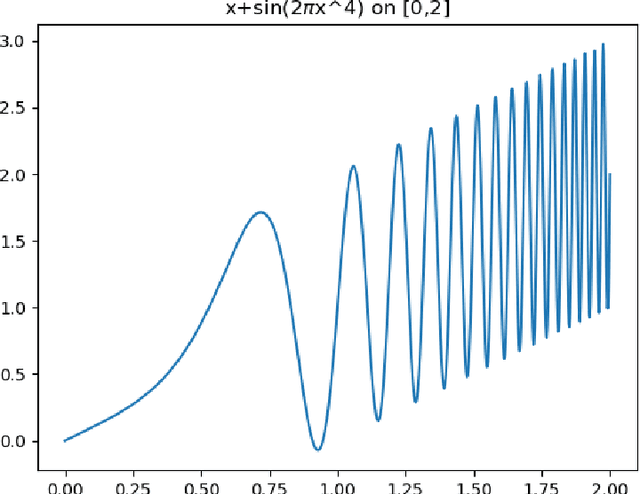
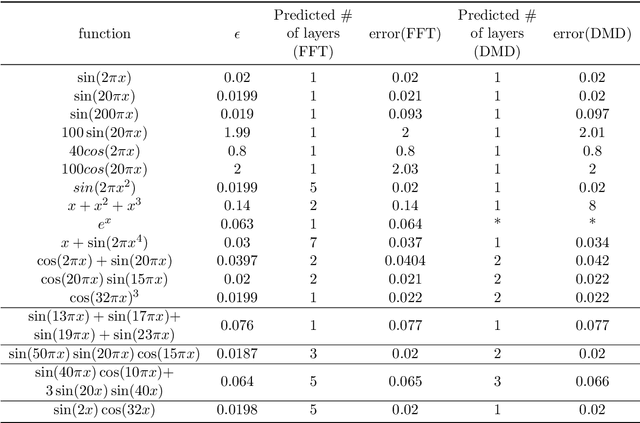
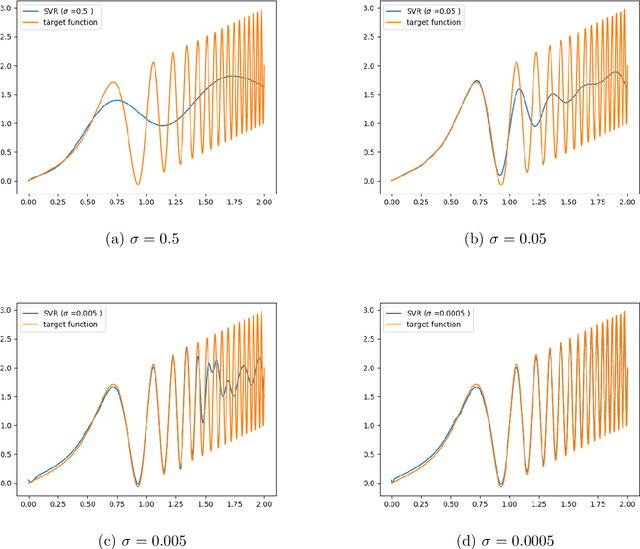
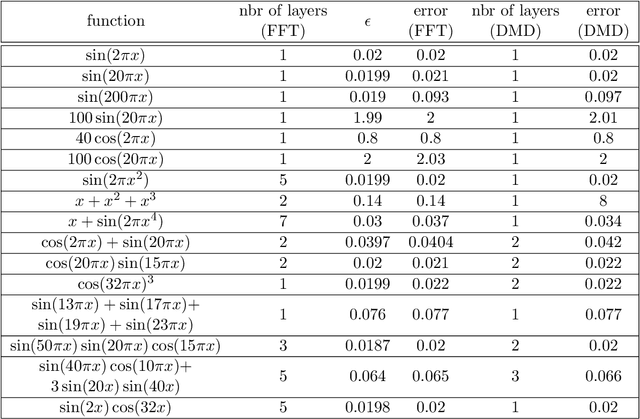
Hierarchical support vector regression (HSVR) models a function from data as a linear combination of SVR models at a range of scales, starting at a coarse scale and moving to finer scales as the hierarchy continues. In the original formulation of HSVR, there were no rules for choosing the depth of the model. In this paper, we observe in a number of models a phase transition in the training error -- the error remains relatively constant as layers are added, until a critical scale is passed, at which point the training error drops close to zero and remains nearly constant for added layers. We introduce a method to predict this critical scale a priori with the prediction based on the support of either a Fourier transform of the data or the Dynamic Mode Decomposition (DMD) spectrum. This allows us to determine the required number of layers prior to training any models.

Modeling, Reduction, and Control of a Helically Actuated Inertial Soft Robotic Arm via the Koopman Operator

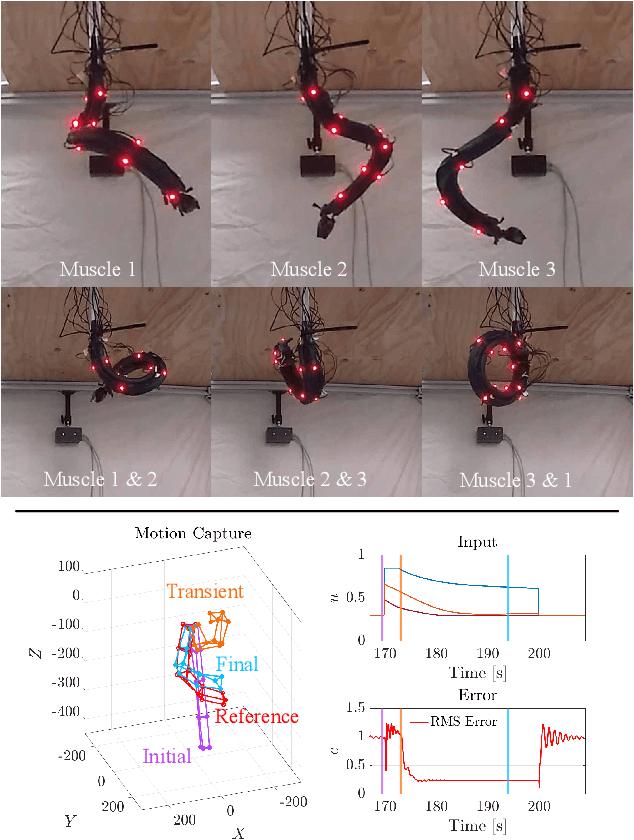
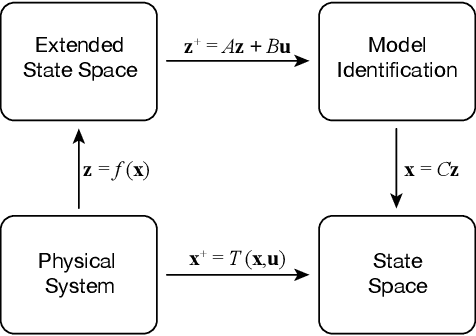
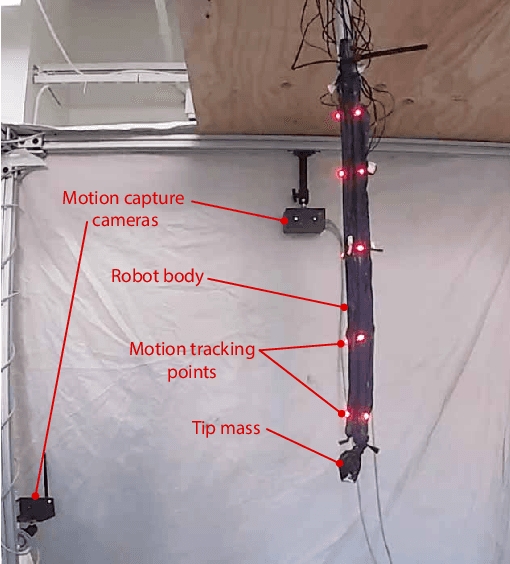
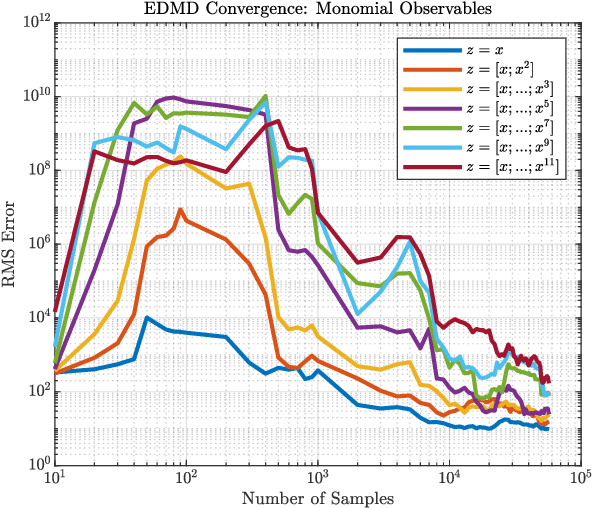
Soft robots promise improved safety and capability over rigid robots when deployed in complex, delicate, and dynamic environments. However, the infinite degrees of freedom and highly nonlinear dynamics of these systems severely complicate their modeling and control. As a step toward addressing this open challenge, we apply the data-driven, Hankel Dynamic Mode Decomposition (HDMD) with time delay observables to the model identification of a highly inertial, helical soft robotic arm with a high number of underactuated degrees of freedom. The resulting model is linear and hence amenable to control via a Linear Quadratic Regulator (LQR). Using our test bed device, a dynamic, lightweight pneumatic fabric arm with an inertial mass at the tip, we show that the combination of HDMD and LQR allows us to command our robot to achieve arbitrary poses using only open loop control. We further show that Koopman spectral analysis gives us a dimensionally reduced basis of modes which decreases computational complexity without sacrificing predictive power.

Applications of Koopman Mode Analysis to Neural Networks

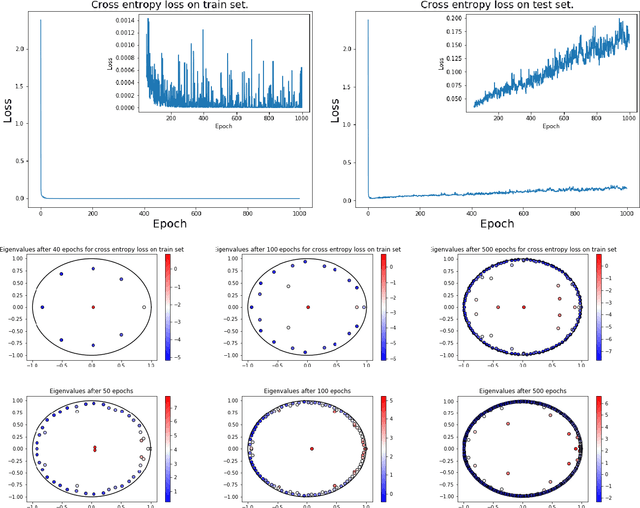
We consider the training process of a neural network as a dynamical system acting on the high-dimensional weight space. Each epoch is an application of the map induced by the optimization algorithm and the loss function. Using this induced map, we can apply observables on the weight space and measure their evolution. The evolution of the observables are given by the Koopman operator associated with the induced dynamical system. We use the spectrum and modes of the Koopman operator to realize the above objectives. Our methods can help to, a priori, determine the network depth; determine if we have a bad initialization of the network weights, allowing a restart before training too long; speeding up the training time. Additionally, our methods help enable noise rejection and improve robustness. We show how the Koopman spectrum can be used to determine the number of layers required for the architecture. Additionally, we show how we can elucidate the convergence versus non-convergence of the training process by monitoring the spectrum, in particular, how the existence of eigenvalues clustering around 1 determines when to terminate the learning process. We also show how using Koopman modes we can selectively prune the network to speed up the training procedure. Finally, we show that incorporating loss functions based on negative Sobolev norms can allow for the reconstruction of a multi-scale signal polluted by very large amounts of noise.

Search strategy in a complex and dynamic environment: the MH370 case

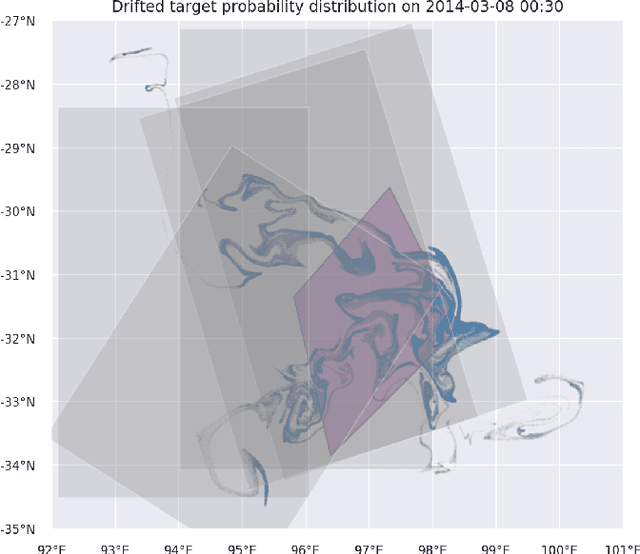
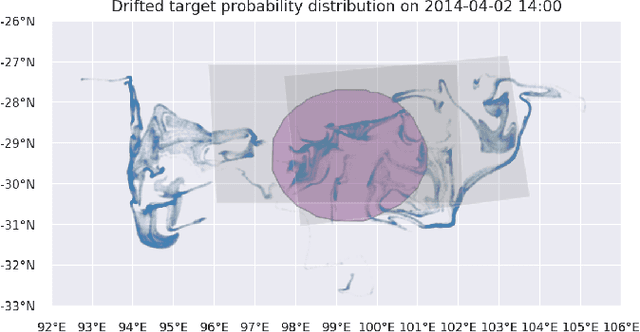
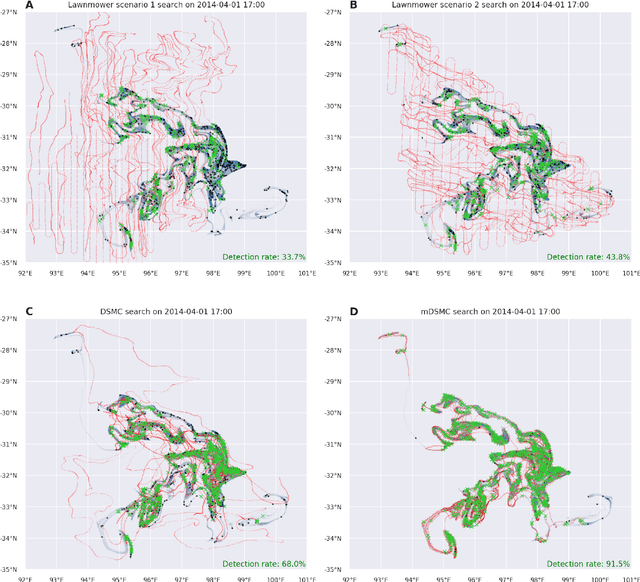
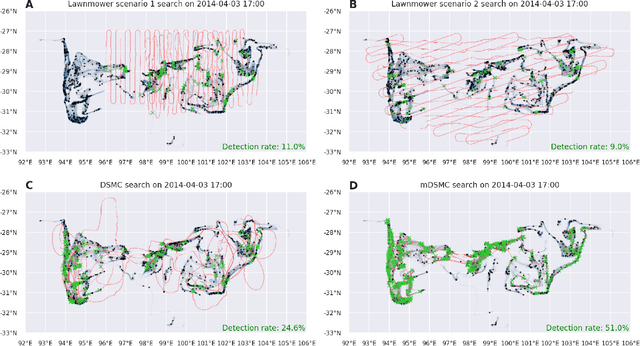
Search and detection of objects on the ocean surface is a challenging task due to the complexity of the drift dynamics and lack of known optimal solutions for the path of the search agents. This challenge was highlighted by the unsuccessful search for Malaysian Flight 370 (MH370) which disappeared on March 8, 2014. In this paper, we propose an improvement of a search algorithm rooted in the ergodic theory of dynamical systems which can accommodate complex geometries and uncertainties of the drifting search areas on the ocean surface. We illustrate the effectiveness of this algorithm in a computational replication of the conducted search for MH370. In comparison to conventional search methods, the proposed algorithm leads to an order of magnitude improvement in success rate over the time period of the actual search operation. Simulations of the proposed search control also indicate that the initial success rate of finding debris increases in the event of delayed search commencement. This is due to the existence of convergence zones in the search area which leads to local aggregation of debris in those zones and hence reduction of the effective size of the area to be searched.