Trajectory Estimation in Unknown Nonlinear Manifold Using Koopman Operator Theory

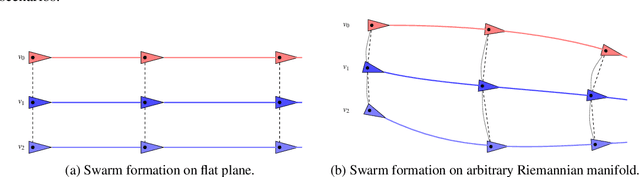
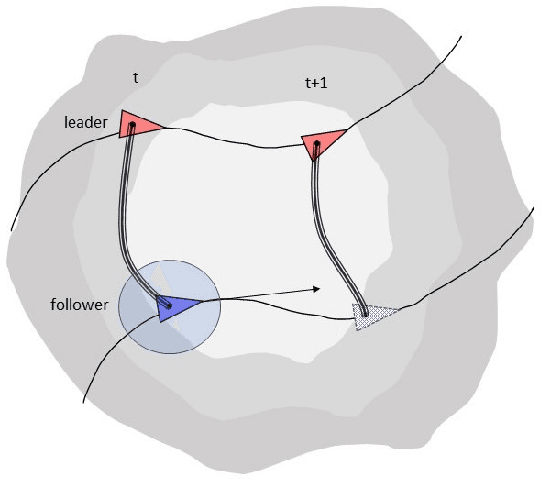
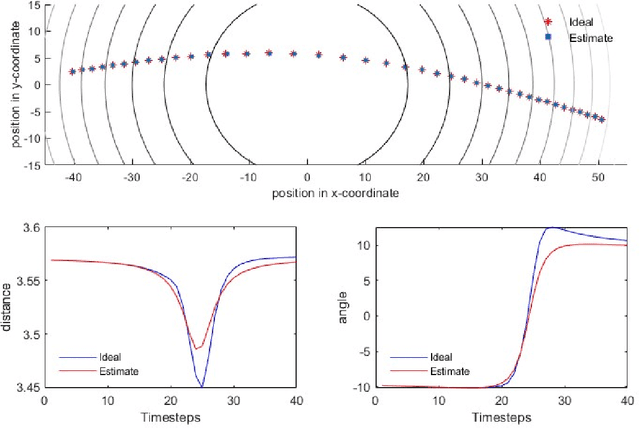
Formation coordination is a critical aspect of swarm robotics, which involves coordinating the motion and behavior of a group of robots to achieve a specific objective. In formation coordination, the robots must maintain a specific spatial arrangement while in motion. In this paper, we present a leader-follower column formation coordination problem in an unknown, two-dimensional nonlinear manifold, where we redefining it as a trajectory estimation problem. Leveraging Koopman operator theory and Extended Dynamic Mode Decomposition, we estimate the measurement vectors for the follower agent and guide its nonlinear trajectories.

Modeling, Reduction, and Control of a Helically Actuated Inertial Soft Robotic Arm via the Koopman Operator

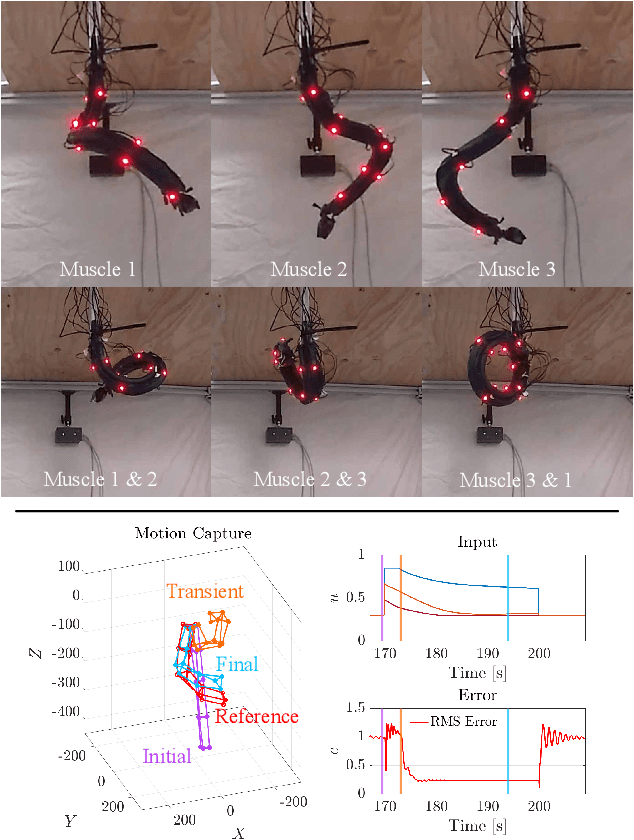
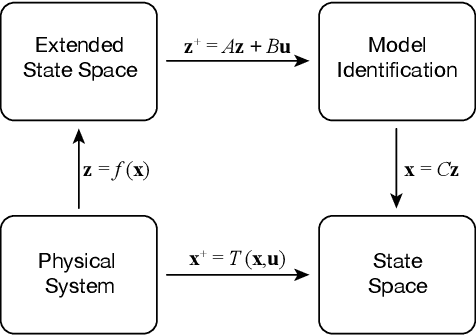
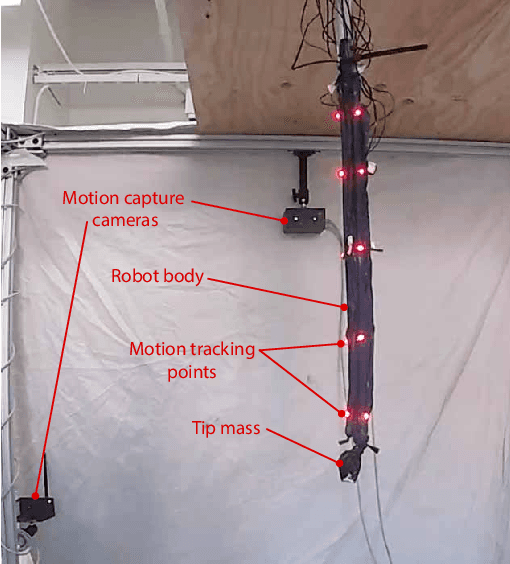
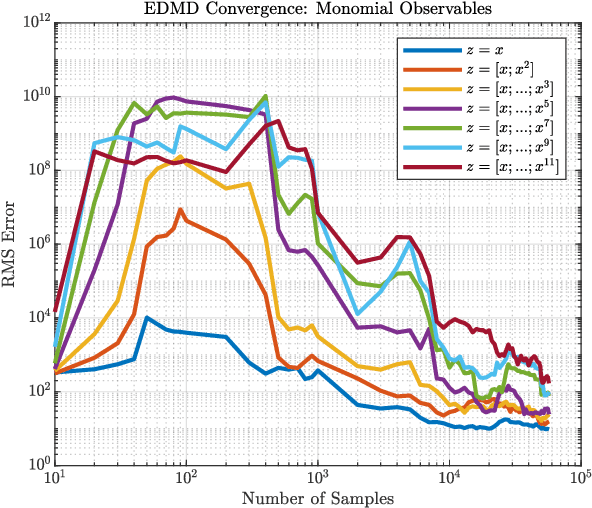
Soft robots promise improved safety and capability over rigid robots when deployed in complex, delicate, and dynamic environments. However, the infinite degrees of freedom and highly nonlinear dynamics of these systems severely complicate their modeling and control. As a step toward addressing this open challenge, we apply the data-driven, Hankel Dynamic Mode Decomposition (HDMD) with time delay observables to the model identification of a highly inertial, helical soft robotic arm with a high number of underactuated degrees of freedom. The resulting model is linear and hence amenable to control via a Linear Quadratic Regulator (LQR). Using our test bed device, a dynamic, lightweight pneumatic fabric arm with an inertial mass at the tip, we show that the combination of HDMD and LQR allows us to command our robot to achieve arbitrary poses using only open loop control. We further show that Koopman spectral analysis gives us a dimensionally reduced basis of modes which decreases computational complexity without sacrificing predictive power.