Trajectory Estimation in Unknown Nonlinear Manifold Using Koopman Operator Theory

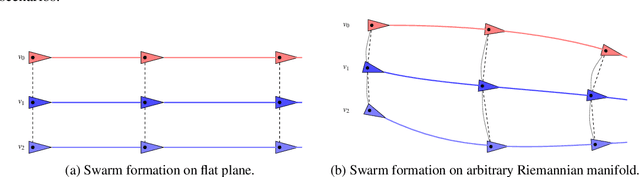
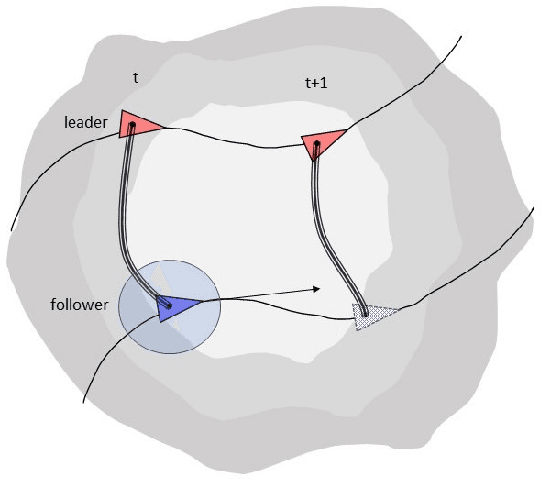
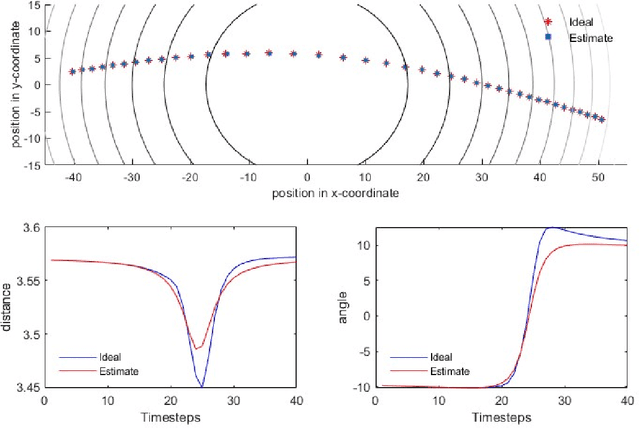
Formation coordination is a critical aspect of swarm robotics, which involves coordinating the motion and behavior of a group of robots to achieve a specific objective. In formation coordination, the robots must maintain a specific spatial arrangement while in motion. In this paper, we present a leader-follower column formation coordination problem in an unknown, two-dimensional nonlinear manifold, where we redefining it as a trajectory estimation problem. Leveraging Koopman operator theory and Extended Dynamic Mode Decomposition, we estimate the measurement vectors for the follower agent and guide its nonlinear trajectories.

An Operator Theoretic Perspective on Pruning Deep Neural Networks

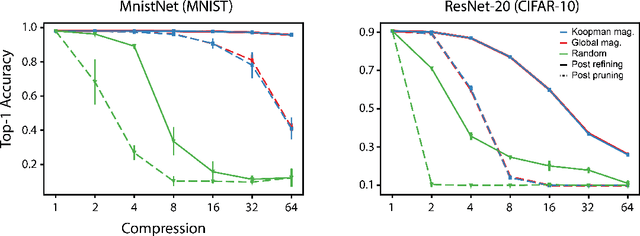
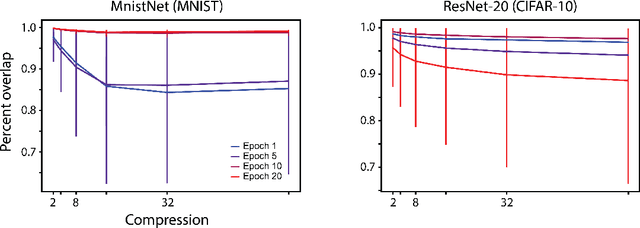
The discovery of sparse subnetworks that are able to perform as well as full models has found broad applied and theoretical interest. While many pruning methods have been developed to this end, the na\"ive approach of removing parameters based on their magnitude has been found to be as robust as more complex, state-of-the-art algorithms. The lack of theory behind magnitude pruning's success, especially pre-convergence, and its relation to other pruning methods, such as gradient based pruning, are outstanding open questions in the field that are in need of being addressed. We make use of recent advances in dynamical systems theory, namely Koopman operator theory, to define a new class of theoretically motivated pruning algorithms. We show that these algorithms can be equivalent to magnitude and gradient based pruning, unifying these seemingly disparate methods, and that they can be used to shed light on magnitude pruning's performance during early training.