On Equivalent Optimization of Machine Learning Methods

At the core of many machine learning methods resides an iterative optimization algorithm for their training. Such optimization algorithms often come with a plethora of choices regarding their implementation. In the case of deep neural networks, choices of optimizer, learning rate, batch size, etc. must be made. Despite the fundamental way in which these choices impact the training of deep neural networks, there exists no general method for identifying when they lead to equivalent, or non-equivalent, optimization trajectories. By viewing iterative optimization as a discrete-time dynamical system, we are able to leverage Koopman operator theory, where it is known that conjugate dynamics can have identical spectral objects. We find highly overlapping Koopman spectra associated with the application of online mirror and gradient descent to specific problems, illustrating that such a data-driven approach can corroborate the recently discovered analytical equivalence between the two optimizers. We extend our analysis to feedforward, fully connected neural networks, providing the first general characterization of when choices of learning rate, batch size, layer width, data set, and activation function lead to equivalent, and non-equivalent, evolution of network parameters during training. Among our main results, we find that learning rate to batch size ratio, layer width, nature of data set (handwritten vs. synthetic), and activation function affect the nature of conjugacy. Our data-driven approach is general and can be utilized broadly to compare the optimization of machine learning methods.

An Operator Theoretic Perspective on Pruning Deep Neural Networks

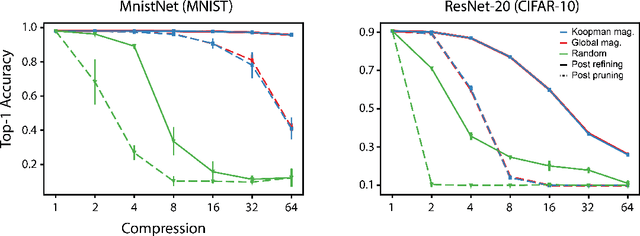
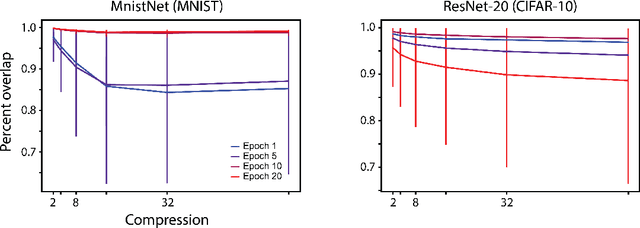
The discovery of sparse subnetworks that are able to perform as well as full models has found broad applied and theoretical interest. While many pruning methods have been developed to this end, the na\"ive approach of removing parameters based on their magnitude has been found to be as robust as more complex, state-of-the-art algorithms. The lack of theory behind magnitude pruning's success, especially pre-convergence, and its relation to other pruning methods, such as gradient based pruning, are outstanding open questions in the field that are in need of being addressed. We make use of recent advances in dynamical systems theory, namely Koopman operator theory, to define a new class of theoretically motivated pruning algorithms. We show that these algorithms can be equivalent to magnitude and gradient based pruning, unifying these seemingly disparate methods, and that they can be used to shed light on magnitude pruning's performance during early training.

Predicting the Critical Number of Layers for Hierarchical Support Vector Regression

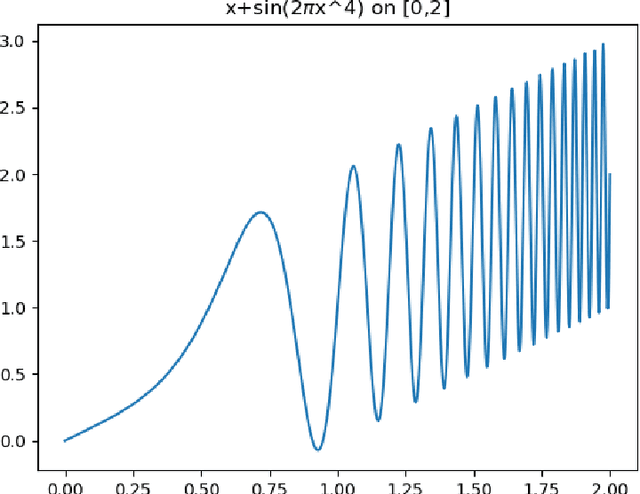
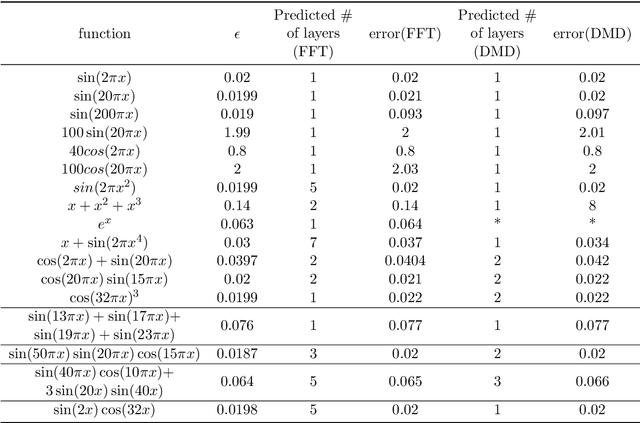
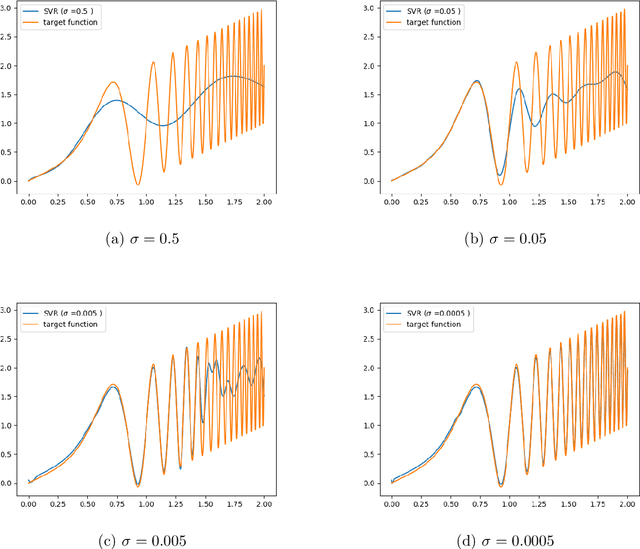
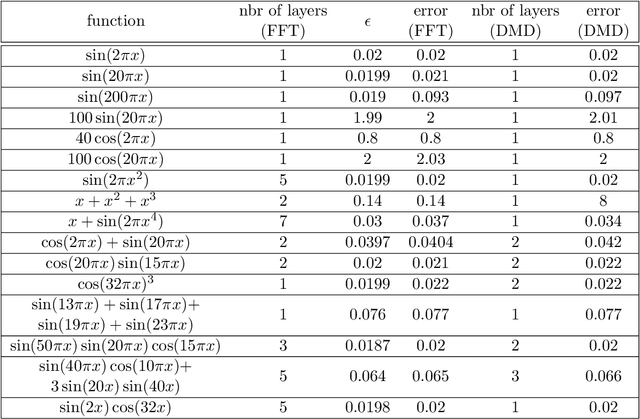
Hierarchical support vector regression (HSVR) models a function from data as a linear combination of SVR models at a range of scales, starting at a coarse scale and moving to finer scales as the hierarchy continues. In the original formulation of HSVR, there were no rules for choosing the depth of the model. In this paper, we observe in a number of models a phase transition in the training error -- the error remains relatively constant as layers are added, until a critical scale is passed, at which point the training error drops close to zero and remains nearly constant for added layers. We introduce a method to predict this critical scale a priori with the prediction based on the support of either a Fourier transform of the data or the Dynamic Mode Decomposition (DMD) spectrum. This allows us to determine the required number of layers prior to training any models.

Applications of Koopman Mode Analysis to Neural Networks

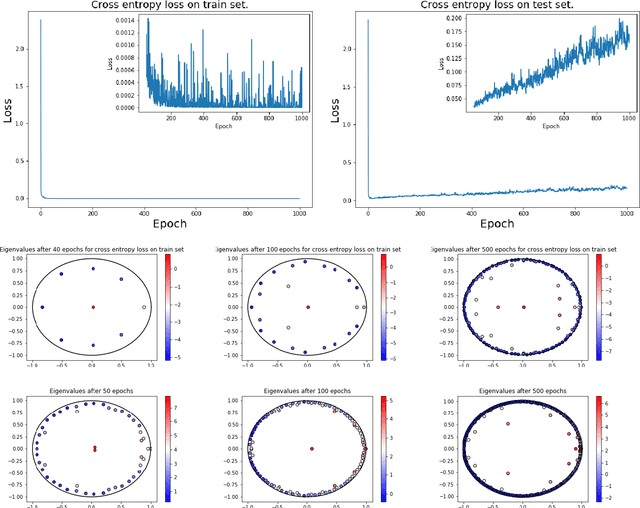
We consider the training process of a neural network as a dynamical system acting on the high-dimensional weight space. Each epoch is an application of the map induced by the optimization algorithm and the loss function. Using this induced map, we can apply observables on the weight space and measure their evolution. The evolution of the observables are given by the Koopman operator associated with the induced dynamical system. We use the spectrum and modes of the Koopman operator to realize the above objectives. Our methods can help to, a priori, determine the network depth; determine if we have a bad initialization of the network weights, allowing a restart before training too long; speeding up the training time. Additionally, our methods help enable noise rejection and improve robustness. We show how the Koopman spectrum can be used to determine the number of layers required for the architecture. Additionally, we show how we can elucidate the convergence versus non-convergence of the training process by monitoring the spectrum, in particular, how the existence of eigenvalues clustering around 1 determines when to terminate the learning process. We also show how using Koopman modes we can selectively prune the network to speed up the training procedure. Finally, we show that incorporating loss functions based on negative Sobolev norms can allow for the reconstruction of a multi-scale signal polluted by very large amounts of noise.