Micro-Macro Consistency in Multiscale Modeling: Score-Based Model Assisted Sampling of Fast/Slow Dynamical Systems

A valuable step in the modeling of multiscale dynamical systems in fields such as computational chemistry, biology, materials science and more, is the representative sampling of the phase space over long timescales of interest; this task is not, however, without challenges. For example, the long term behavior of a system with many degrees of freedom often cannot be efficiently computationally explored by direct dynamical simulation; such systems can often become trapped in local free energy minima. In the study of physics-based multi-time-scale dynamical systems, techniques have been developed for enhancing sampling in order to accelerate exploration beyond free energy barriers. On the other hand, in the field of Machine Learning, a generic goal of generative models is to sample from a target density, after training on empirical samples from this density. Score based generative models (SGMs) have demonstrated state-of-the-art capabilities in generating plausible data from target training distributions. Conditional implementations of such generative models have been shown to exhibit significant parallels with long-established -- and physics based -- solutions to enhanced sampling. These physics-based methods can then be enhanced through coupling with the ML generative models, complementing the strengths and mitigating the weaknesses of each technique. In this work, we show that that SGMs can be used in such a coupling framework to improve sampling in multiscale dynamical systems.

Tipping Points of Evolving Epidemiological Networks: Machine Learning-Assisted, Data-Driven Effective Modeling

We study the tipping point collective dynamics of an adaptive susceptible-infected-susceptible (SIS) epidemiological network in a data-driven, machine learning-assisted manner. We identify a parameter-dependent effective stochastic differential equation (eSDE) in terms of physically meaningful coarse mean-field variables through a deep-learning ResNet architecture inspired by numerical stochastic integrators. We construct an approximate effective bifurcation diagram based on the identified drift term of the eSDE and contrast it with the mean-field SIS model bifurcation diagram. We observe a subcritical Hopf bifurcation in the evolving network's effective SIS dynamics, that causes the tipping point behavior; this takes the form of large amplitude collective oscillations that spontaneously -- yet rarely -- arise from the neighborhood of a (noisy) stationary state. We study the statistics of these rare events both through repeated brute force simulations and by using established mathematical/computational tools exploiting the right-hand-side of the identified SDE. We demonstrate that such a collective SDE can also be identified (and the rare events computations also performed) in terms of data-driven coarse observables, obtained here via manifold learning techniques, in particular Diffusion Maps. The workflow of our study is straightforwardly applicable to other complex dynamics problems exhibiting tipping point dynamics.

Tasks Makyth Models: Machine Learning Assisted Surrogates for Tipping Points

We present a machine learning (ML)-assisted framework bridging manifold learning, neural networks, Gaussian processes, and Equation-Free multiscale modeling, for (a) detecting tipping points in the emergent behavior of complex systems, and (b) characterizing probabilities of rare events (here, catastrophic shifts) near them. Our illustrative example is an event-driven, stochastic agent-based model (ABM) describing the mimetic behavior of traders in a simple financial market. Given high-dimensional spatiotemporal data -- generated by the stochastic ABM -- we construct reduced-order models for the emergent dynamics at different scales: (a) mesoscopic Integro-Partial Differential Equations (IPDEs); and (b) mean-field-type Stochastic Differential Equations (SDEs) embedded in a low-dimensional latent space, targeted to the neighborhood of the tipping point. We contrast the uses of the different models and the effort involved in learning them.

On Equivalent Optimization of Machine Learning Methods

At the core of many machine learning methods resides an iterative optimization algorithm for their training. Such optimization algorithms often come with a plethora of choices regarding their implementation. In the case of deep neural networks, choices of optimizer, learning rate, batch size, etc. must be made. Despite the fundamental way in which these choices impact the training of deep neural networks, there exists no general method for identifying when they lead to equivalent, or non-equivalent, optimization trajectories. By viewing iterative optimization as a discrete-time dynamical system, we are able to leverage Koopman operator theory, where it is known that conjugate dynamics can have identical spectral objects. We find highly overlapping Koopman spectra associated with the application of online mirror and gradient descent to specific problems, illustrating that such a data-driven approach can corroborate the recently discovered analytical equivalence between the two optimizers. We extend our analysis to feedforward, fully connected neural networks, providing the first general characterization of when choices of learning rate, batch size, layer width, data set, and activation function lead to equivalent, and non-equivalent, evolution of network parameters during training. Among our main results, we find that learning rate to batch size ratio, layer width, nature of data set (handwritten vs. synthetic), and activation function affect the nature of conjugacy. Our data-driven approach is general and can be utilized broadly to compare the optimization of machine learning methods.

Gentlest ascent dynamics on manifolds defined by adaptively sampled point-clouds

Finding saddle points of dynamical systems is an important problem in practical applications such as the study of rare events of molecular systems. Gentlest ascent dynamics (GAD) is one of a number of algorithms in existence that attempt to find saddle points in dynamical systems. It works by deriving a new dynamical system in which saddle points of the original system become stable equilibria. GAD has been recently generalized to the study of dynamical systems on manifolds (differential algebraic equations) described by equality constraints and given an extrinsic formulation. In this paper, we present an extension of GAD to manifolds defined by point-clouds and formulated intrinsically. These point-clouds are adaptively sampled during an iterative process that drives the system from the initial conformation (typically in the neighborhood of a stable equilibrium) to a saddle point. Our method requires the reactant (initial conformation), does not require the explicit constraint equations to be specified, and is purely data-driven.

GANs and Closures: Micro-Macro Consistency in Multiscale Modeling

Sampling the phase space of molecular systems -- and, more generally, of complex systems effectively modeled by stochastic differential equations -- is a crucial modeling step in many fields, from protein folding to materials discovery. These problems are often multiscale in nature: they can be described in terms of low-dimensional effective free energy surfaces parametrized by a small number of "slow" reaction coordinates; the remaining "fast" degrees of freedom populate an equilibrium measure on the reaction coordinate values. Sampling procedures for such problems are used to estimate effective free energy differences as well as ensemble averages with respect to the conditional equilibrium distributions; these latter averages lead to closures for effective reduced dynamic models. Over the years, enhanced sampling techniques coupled with molecular simulation have been developed. An intriguing analogy arises with the field of Machine Learning (ML), where Generative Adversarial Networks can produce high dimensional samples from low dimensional probability distributions. This sample generation returns plausible high dimensional space realizations of a model state, from information about its low-dimensional representation. In this work, we present an approach that couples physics-based simulations and biasing methods for sampling conditional distributions with ML-based conditional generative adversarial networks for the same task. The "coarse descriptors" on which we condition the fine scale realizations can either be known a priori, or learned through nonlinear dimensionality reduction. We suggest that this may bring out the best features of both approaches: we demonstrate that a framework that couples cGANs with physics-based enhanced sampling techniques can improve multiscale SDE dynamical systems sampling, and even shows promise for systems of increasing complexity.

Learning Effective SDEs from Brownian Dynamics Simulations of Colloidal Particles

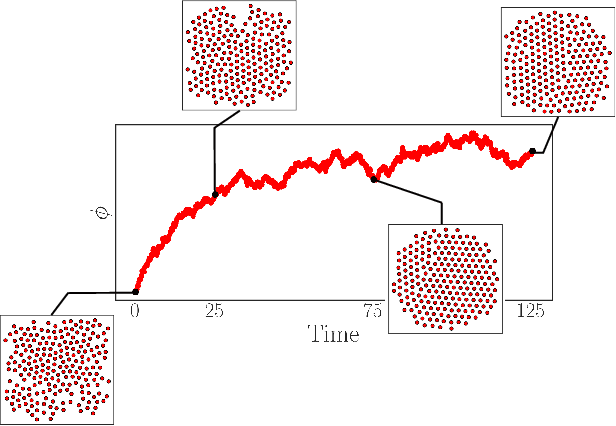
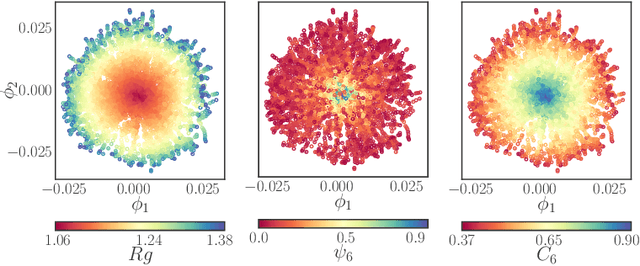
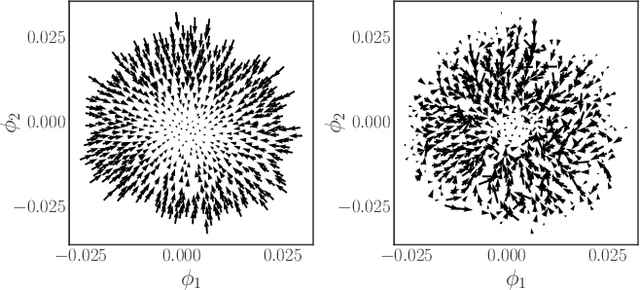
We construct a reduced, data-driven, parameter dependent effective Stochastic Differential Equation (eSDE) for electric-field mediated colloidal crystallization using data obtained from Brownian Dynamics Simulations. We use Diffusion Maps (a manifold learning algorithm) to identify a set of useful latent observables. In this latent space we identify an eSDE using a deep learning architecture inspired by numerical stochastic integrators and compare it with the traditional Kramers-Moyal expansion estimation. We show that the obtained variables and the learned dynamics accurately encode the physics of the Brownian Dynamic Simulations. We further illustrate that our reduced model captures the dynamics of corresponding experimental data. Our dimension reduction/reduced model identification approach can be easily ported to a broad class of particle systems dynamics experiments/models.

Staying the course: Locating equilibria of dynamical systems on Riemannian manifolds defined by point-clouds

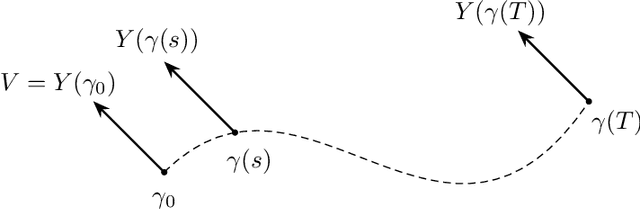
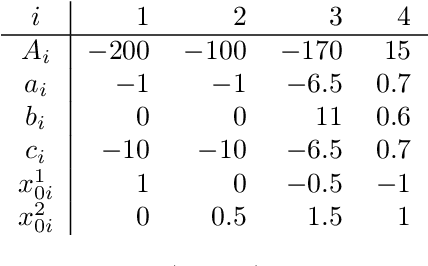
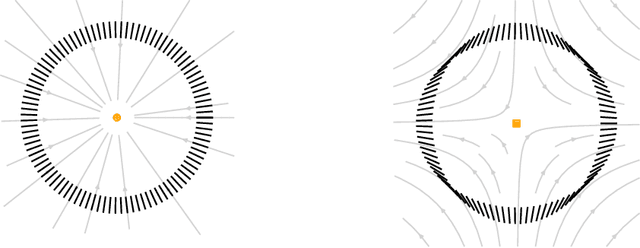
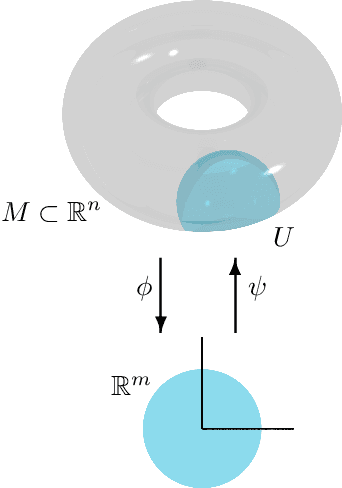
We introduce a method to successively locate equilibria (steady states) of dynamical systems on Riemannian manifolds. The manifolds need not be characterized by an atlas or by the zeros of a smooth map. Instead, they can be defined by point-clouds and sampled as needed through an iterative process. If the manifold is an Euclidean space, our method follows isoclines, curves along which the direction of the vector field $X$ is constant. For a generic vector field $X$, isoclines are smooth curves and every equilibrium is a limit point of isoclines. We generalize the definition of isoclines to Riemannian manifolds through the use of parallel transport: generalized isoclines are curves along which the directions of $X$ are parallel transports of each other. As in the Euclidean case, generalized isoclines of generic vector fields $X$ are smooth curves that connect equilibria of $X$. Our work is motivated by computational statistical mechanics, specifically high dimensional (stochastic) differential equations that model the dynamics of molecular systems. Often, these dynamics concentrate near low-dimensional manifolds and have transitions (sadddle points with a single unstable direction) between metastable equilibria We employ iteratively sampled data and isoclines to locate these saddle points. Coupling a black-box sampling scheme (e.g., Markov chain Monte Carlo) with manifold learning techniques (diffusion maps in the case presented here), we show that our method reliably locates equilibria of $X$.

On the Correspondence between Gaussian Processes and Geometric Harmonics

We discuss the correspondence between Gaussian process regression and Geometric Harmonics, two similar kernel-based methods that are typically used in different contexts. Research communities surrounding the two concepts often pursue different goals. Results from both camps can be successfully combined, providing alternative interpretations of uncertainty in terms of error estimation, or leading towards accelerated Bayesian Optimization due to dimensionality reduction.