Staying the course: Locating equilibria of dynamical systems on Riemannian manifolds defined by point-clouds
Paper and Code
Apr 21, 2022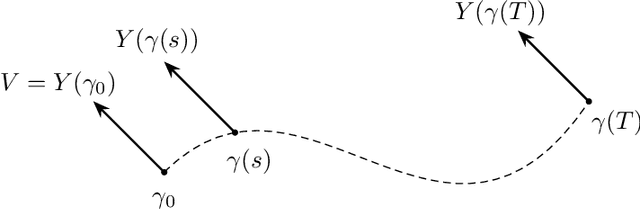
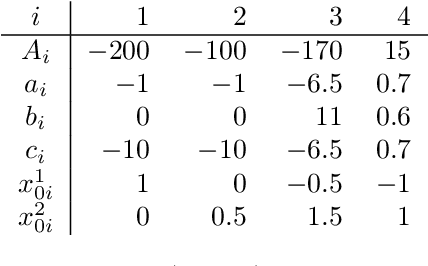
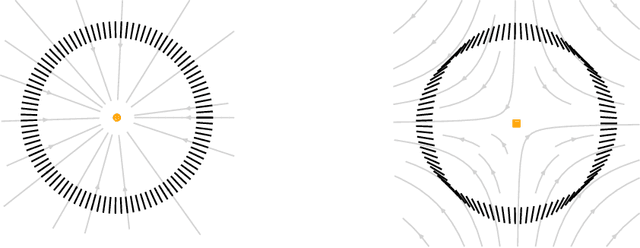
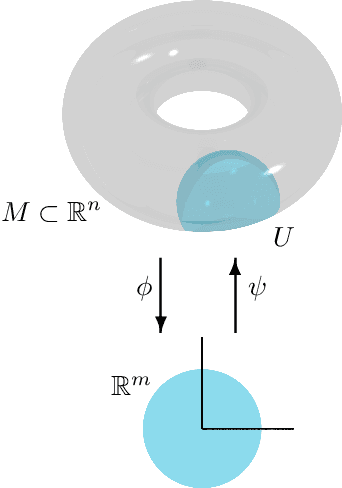
We introduce a method to successively locate equilibria (steady states) of dynamical systems on Riemannian manifolds. The manifolds need not be characterized by an atlas or by the zeros of a smooth map. Instead, they can be defined by point-clouds and sampled as needed through an iterative process. If the manifold is an Euclidean space, our method follows isoclines, curves along which the direction of the vector field $X$ is constant. For a generic vector field $X$, isoclines are smooth curves and every equilibrium is a limit point of isoclines. We generalize the definition of isoclines to Riemannian manifolds through the use of parallel transport: generalized isoclines are curves along which the directions of $X$ are parallel transports of each other. As in the Euclidean case, generalized isoclines of generic vector fields $X$ are smooth curves that connect equilibria of $X$. Our work is motivated by computational statistical mechanics, specifically high dimensional (stochastic) differential equations that model the dynamics of molecular systems. Often, these dynamics concentrate near low-dimensional manifolds and have transitions (sadddle points with a single unstable direction) between metastable equilibria We employ iteratively sampled data and isoclines to locate these saddle points. Coupling a black-box sampling scheme (e.g., Markov chain Monte Carlo) with manifold learning techniques (diffusion maps in the case presented here), we show that our method reliably locates equilibria of $X$.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge