Deterministic Global Optimization of the Acquisition Function in Bayesian Optimization: To Do or Not To Do?

Bayesian Optimization (BO) with Gaussian Processes relies on optimizing an acquisition function to determine sampling. We investigate the advantages and disadvantages of using a deterministic global solver (MAiNGO) compared to conventional local and stochastic global solvers (L-BFGS-B and multi-start, respectively) for the optimization of the acquisition function. For CPU efficiency, we set a time limit for MAiNGO, taking the best point as optimal. We perform repeated numerical experiments, initially using the Muller-Brown potential as a benchmark function, utilizing the lower confidence bound acquisition function; we further validate our findings with three alternative benchmark functions. Statistical analysis reveals that when the acquisition function is more exploitative (as opposed to exploratory), BO with MAiNGO converges in fewer iterations than with the local solvers. However, when the dataset lacks diversity, or when the acquisition function is overly exploitative, BO with MAiNGO, compared to the local solvers, is more likely to converge to a local rather than a global ly near-optimal solution of the black-box function. L-BFGS-B and multi-start mitigate this risk in BO by introducing stochasticity in the selection of the next sampling point, which enhances the exploration of uncharted regions in the search space and reduces dependence on acquisition function hyperparameters. Ultimately, suboptimal optimization of poorly chosen acquisition functions may be preferable to their optimal solution. When the acquisition function is more exploratory, BO with MAiNGO, multi-start, and L-BFGS-B achieve comparable probabilities of convergence to a globally near-optimal solution (although BO with MAiNGO may require more iterations to converge under these conditions).

Gentlest ascent dynamics on manifolds defined by adaptively sampled point-clouds

Finding saddle points of dynamical systems is an important problem in practical applications such as the study of rare events of molecular systems. Gentlest ascent dynamics (GAD) is one of a number of algorithms in existence that attempt to find saddle points in dynamical systems. It works by deriving a new dynamical system in which saddle points of the original system become stable equilibria. GAD has been recently generalized to the study of dynamical systems on manifolds (differential algebraic equations) described by equality constraints and given an extrinsic formulation. In this paper, we present an extension of GAD to manifolds defined by point-clouds and formulated intrinsically. These point-clouds are adaptively sampled during an iterative process that drives the system from the initial conformation (typically in the neighborhood of a stable equilibrium) to a saddle point. Our method requires the reactant (initial conformation), does not require the explicit constraint equations to be specified, and is purely data-driven.

Staying the course: Locating equilibria of dynamical systems on Riemannian manifolds defined by point-clouds

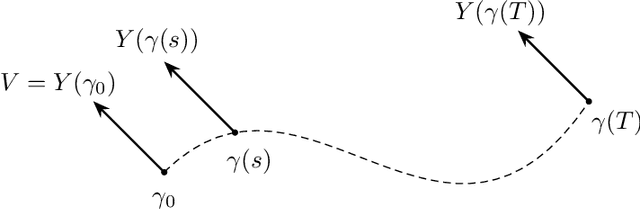
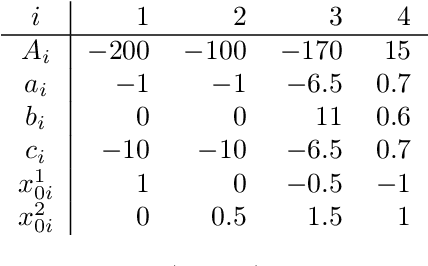
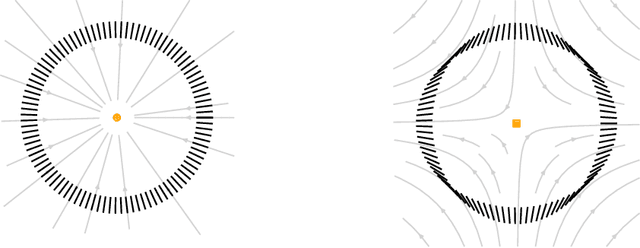
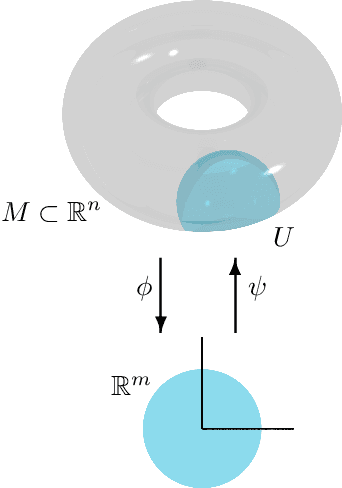
We introduce a method to successively locate equilibria (steady states) of dynamical systems on Riemannian manifolds. The manifolds need not be characterized by an atlas or by the zeros of a smooth map. Instead, they can be defined by point-clouds and sampled as needed through an iterative process. If the manifold is an Euclidean space, our method follows isoclines, curves along which the direction of the vector field $X$ is constant. For a generic vector field $X$, isoclines are smooth curves and every equilibrium is a limit point of isoclines. We generalize the definition of isoclines to Riemannian manifolds through the use of parallel transport: generalized isoclines are curves along which the directions of $X$ are parallel transports of each other. As in the Euclidean case, generalized isoclines of generic vector fields $X$ are smooth curves that connect equilibria of $X$. Our work is motivated by computational statistical mechanics, specifically high dimensional (stochastic) differential equations that model the dynamics of molecular systems. Often, these dynamics concentrate near low-dimensional manifolds and have transitions (sadddle points with a single unstable direction) between metastable equilibria We employ iteratively sampled data and isoclines to locate these saddle points. Coupling a black-box sampling scheme (e.g., Markov chain Monte Carlo) with manifold learning techniques (diffusion maps in the case presented here), we show that our method reliably locates equilibria of $X$.