Using Linearized Optimal Transport to Predict the Evolution of Stochastic Particle Systems

We develop an algorithm to approximate the time evolution of a probability measure without explicitly learning an operator that governs the evolution. A particular application of interest is discrete measures $\mu_t^N$ that arise from particle systems. In many such situations, the individual particles move chaotically on short time scales, making it difficult to learn the dynamics of a governing operator, but the bulk distribution $\mu_t^N$ approximates an absolutely continuous measure $\mu_t$ that evolves ``smoothly.'' If $\mu_t$ is known on some time interval, then linearized optimal transport theory provides an Euler-like scheme for approximating the evolution of $\mu_t$ using its ``tangent vector field'' (represented as a time-dependent vector field on $\mathbb R^d$), which can be computed as a limit of optimal transport maps. We propose an analog of this Euler approximation to predict the evolution of the discrete measure $\mu_t^N$ (without knowing $\mu_t$). To approximate the analogous tangent vector field, we use a finite difference over a time step that sits between the two time scales of the system -- long enough for the large-$N$ evolution ($\mu_t$) to emerge but short enough to satisfactorily approximate the derivative object used in the Euler scheme. By allowing the limiting behavior to emerge, the optimal transport maps closely approximate the vector field describing the bulk distribution's smooth evolution instead of the individual particles' more chaotic movements. We demonstrate the efficacy of this approach with two illustrative examples, Gaussian diffusion and a cell chemotaxis model, and show that our method succeeds in predicting the bulk behavior over relatively large steps.

On-Manifold Projected Gradient Descent

This work provides a computable, direct, and mathematically rigorous approximation to the differential geometry of class manifolds for high-dimensional data, along with nonlinear projections from input space onto these class manifolds. The tools are applied to the setting of neural network image classifiers, where we generate novel, on-manifold data samples, and implement a projected gradient descent algorithm for on-manifold adversarial training. The susceptibility of neural networks (NNs) to adversarial attack highlights the brittle nature of NN decision boundaries in input space. Introducing adversarial examples during training has been shown to reduce the susceptibility of NNs to adversarial attack; however, it has also been shown to reduce the accuracy of the classifier if the examples are not valid examples for that class. Realistic "on-manifold" examples have been previously generated from class manifolds in the latent of an autoencoder. Our work explores these phenomena in a geometric and computational setting that is much closer to the raw, high-dimensional input space than can be provided by VAE or other black box dimensionality reductions. We employ conformally invariant diffusion maps (CIDM) to approximate class manifolds in diffusion coordinates, and develop the Nystr\"{o}m projection to project novel points onto class manifolds in this setting. On top of the manifold approximation, we leverage the spectral exterior calculus (SEC) to determine geometric quantities such as tangent vectors of the manifold. We use these tools to obtain adversarial examples that reside on a class manifold, yet fool a classifier. These misclassifications then become explainable in terms of human-understandable manipulations within the data, by expressing the on-manifold adversary in the semantic basis on the manifold.

Constructing coarse-scale bifurcation diagrams from spatio-temporal observations of microscopic simulations: A parsimonious machine learning approach

We address a three-tier data-driven approach to solve the inverse problem in complex systems modelling from spatio-temporal data produced by microscopic simulators using machine learning. In the first step, we exploit manifold learning and in particular parsimonious Diffusion Maps using leave-one-out cross-validation (LOOCV) to both identify the intrinsic dimension of the manifold where the emergent dynamics evolve and for feature selection over the parametric space. In the second step, based on the selected features, we learn the right-hand-side of the effective partial differential equations (PDEs) using two machine learning schemes, namely shallow Feedforward Neural Networks (FNNs) with two hidden layers and single-layer Random Projection Networks(RPNNs) which basis functions are constructed using an appropriate random sampling approach. Finally, based on the learned black-box PDE model, we construct the corresponding bifurcation diagram, thus exploiting the numerical bifurcation analysis toolkit. For our illustrations, we implemented the proposed method to construct the one-parameter bifurcation diagram of the 1D FitzHugh-Nagumo PDEs from data generated by $D1Q3$ Lattice Boltzmann simulations. The proposed method was quite effective in terms of numerical accuracy regarding the construction of the coarse-scale bifurcation diagram. Furthermore, the proposed RPNN scheme was $\sim$ 20 to 30 times less costly regarding the training phase than the traditional shallow FNNs, thus arising as a promising alternative to deep learning for solving the inverse problem for high-dimensional PDEs.

Time Series Forecasting Using Manifold Learning

We address a three-tier numerical framework based on manifold learning for the forecasting of high-dimensional time series. At the first step, we embed the time series into a reduced low-dimensional space using a nonlinear manifold learning algorithm such as Locally Linear Embedding and Diffusion Maps. At the second step, we construct reduced-order regression models on the manifold, in particular Multivariate Autoregressive (MVAR) and Gaussian Process Regression (GPR) models, to forecast the embedded dynamics. At the final step, we lift the embedded time series back to the original high-dimensional space using Radial Basis Functions interpolation and Geometric Harmonics. For our illustrations, we test the forecasting performance of the proposed numerical scheme with four sets of time series: three synthetic stochastic ones resembling EEG signals produced from linear and nonlinear stochastic models with different model orders, and one real-world data set containing daily time series of 10 key foreign exchange rates (FOREX) spanning the time period 03/09/2001-29/10/2020. The forecasting performance of the proposed numerical scheme is assessed using the combinations of manifold learning, modelling and lifting approaches. We also provide a comparison with the Principal Component Analysis algorithm as well as with the naive random walk model and the MVAR and GPR models trained and implemented directly in the high-dimensional space.

Coarse-grained and emergent distributed parameter systems from data

We explore the derivation of distributed parameter system evolution laws (and in particular, partial differential operators and associated partial differential equations, PDEs) from spatiotemporal data. This is, of course, a classical identification problem; our focus here is on the use of manifold learning techniques (and, in particular, variations of Diffusion Maps) in conjunction with neural network learning algorithms that allow us to attempt this task when the dependent variables, and even the independent variables of the PDE are not known a priori and must be themselves derived from the data. The similarity measure used in Diffusion Maps for dependent coarse variable detection involves distances between local particle distribution observations; for independent variable detection we use distances between local short-time dynamics. We demonstrate each approach through an illustrative established PDE example. Such variable-free, emergent space identification algorithms connect naturally with equation-free multiscale computation tools.

Particles to Partial Differential Equations Parsimoniously

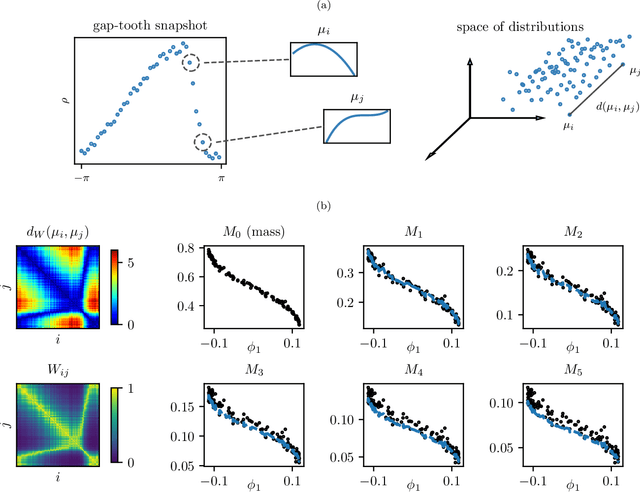
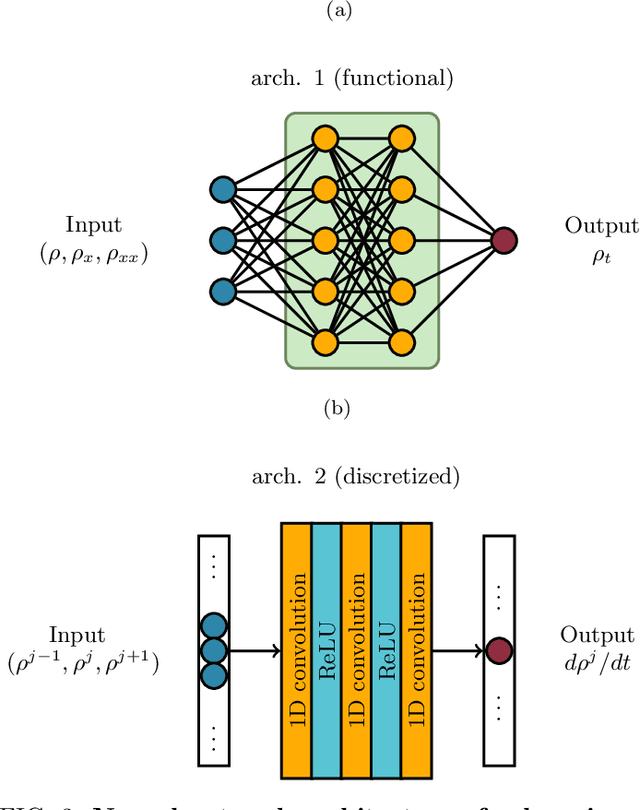
Equations governing physico-chemical processes are usually known at microscopic spatial scales, yet one suspects that there exist equations, e.g. in the form of Partial Differential Equations (PDEs), that can explain the system evolution at much coarser, meso- or macroscopic length scales. Discovering those coarse-grained effective PDEs can lead to considerable savings in computation-intensive tasks like prediction or control. We propose a framework combining artificial neural networks with multiscale computation, in the form of equation-free numerics, for efficient discovery of such macro-scale PDEs directly from microscopic simulations. Gathering sufficient microscopic data for training neural networks can be computationally prohibitive; equation-free numerics enable a more parsimonious collection of training data by only operating in a sparse subset of the space-time domain. We also propose using a data-driven approach, based on manifold learning and unnormalized optimal transport of distributions, to identify macro-scale dependent variable(s) suitable for the data-driven discovery of said PDEs. This approach can corroborate physically motivated candidate variables, or introduce new data-driven variables, in terms of which the coarse-grained effective PDE can be formulated. We illustrate our approach by extracting coarse-grained evolution equations from particle-based simulations with a priori unknown macro-scale variable(s), while significantly reducing the requisite data collection computational effort.