It Takes a Graph to Know a Graph: Rewiring for Homophily with a Reference Graph

Graph Neural Networks (GNNs) excel at analyzing graph-structured data but struggle on heterophilic graphs, where connected nodes often belong to different classes. While this challenge is commonly addressed with specialized GNN architectures, graph rewiring remains an underexplored strategy in this context. We provide theoretical foundations linking edge homophily, GNN embedding smoothness, and node classification performance, motivating the need to enhance homophily. Building on this insight, we introduce a rewiring framework that increases graph homophily using a reference graph, with theoretical guarantees on the homophily of the rewired graph. To broaden applicability, we propose a label-driven diffusion approach for constructing a homophilic reference graph from node features and training labels. Through extensive simulations, we analyze how the homophily of both the original and reference graphs influences the rewired graph homophily and downstream GNN performance. We evaluate our method on 11 real-world heterophilic datasets and show that it outperforms existing rewiring techniques and specialized GNNs for heterophilic graphs, achieving improved node classification accuracy while remaining efficient and scalable to large graphs.

Structure-Aware Matrix Pencil Method

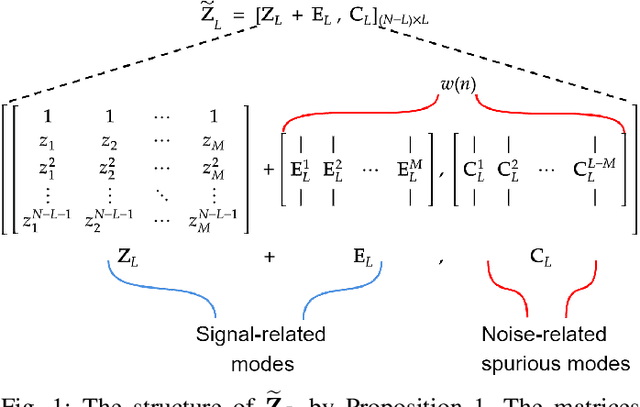
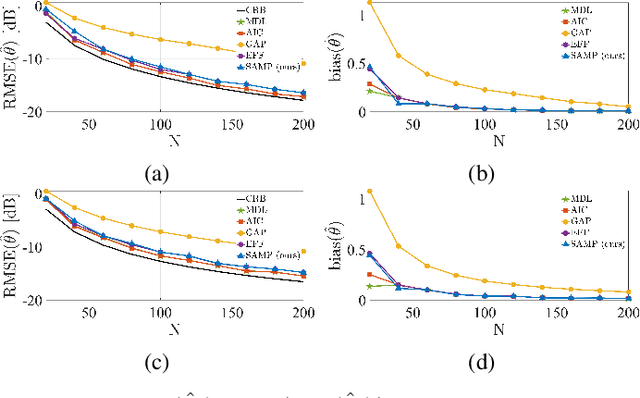
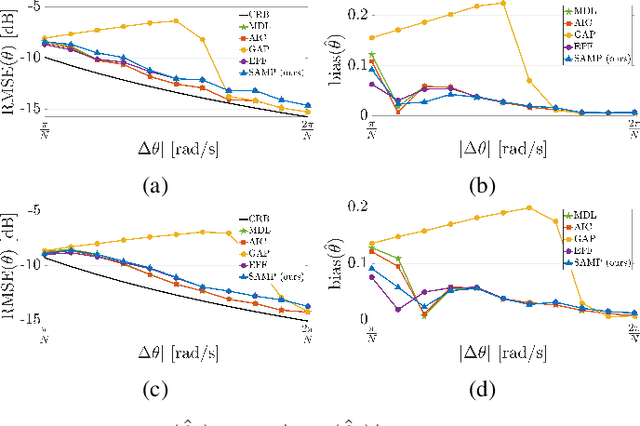
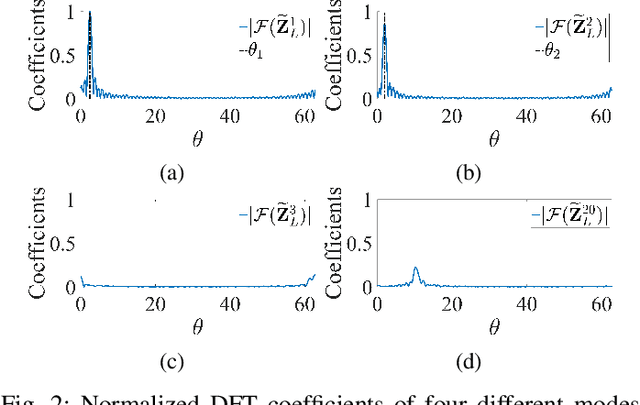
We address the problem of detecting the number of complex exponentials and estimating their parameters from a noisy signal using the Matrix Pencil (MP) method. We introduce the MP modes and present their informative spectral structure. We show theoretically that these modes can be divided into signal and noise modes, where the signal modes exhibit a perturbed Vandermonde structure. Leveraging this structure, we proposed a new MP algorithm, termed the SAMP algorithm, which has two novel components. First, we present a new and robust model order detection with theoretical guarantees. Second, we present an efficient estimation of signal amplitudes. We show empirically that the SAMP algorithm significantly outperforms the standard MP method, particularly in challenging conditions with closely-spaced frequencies and low Signal-to-Noise Ratio (SNR) values, approaching the Cramer-Rao lower bound (CRB) for a broad SNR range. Additionally, compared with prevalent information-based criteria, we show that SAMP is more computationally efficient and insensitive to noise distribution.

Coupled Hierarchical Structure Learning using Tree-Wasserstein Distance

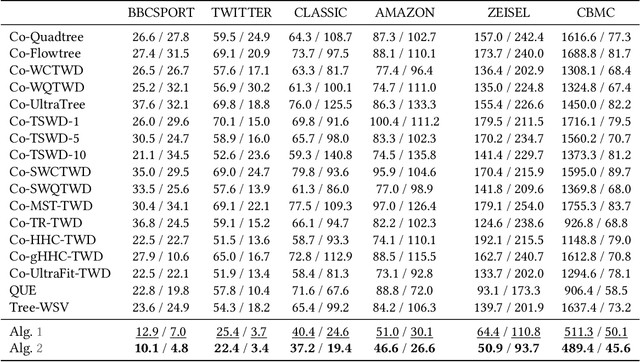
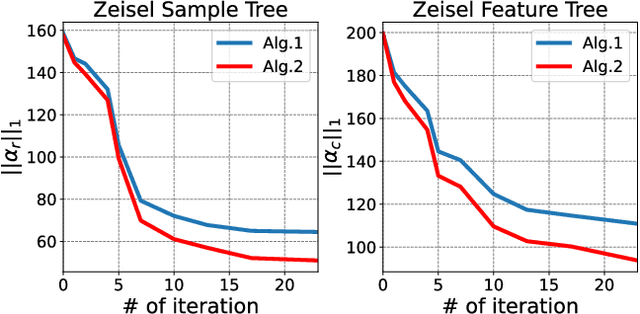
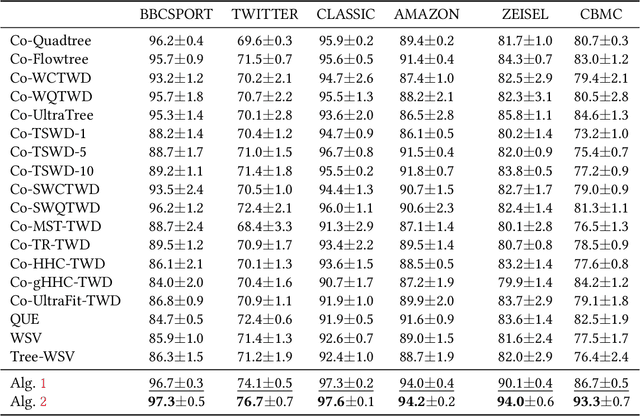
In many applications, both data samples and features have underlying hierarchical structures. However, existing methods for learning these latent structures typically focus on either samples or features, ignoring possible coupling between them. In this paper, we introduce a coupled hierarchical structure learning method using tree-Wasserstein distance (TWD). Our method jointly computes TWDs for samples and features, representing their latent hierarchies as trees. We propose an iterative, unsupervised procedure to build these sample and feature trees based on diffusion geometry, hyperbolic geometry, and wavelet filters. We show that this iterative procedure converges and empirically improves the quality of the constructed trees. The method is also computationally efficient and scales well in high-dimensional settings. Our method can be seamlessly integrated with hyperbolic graph convolutional networks (HGCN). We demonstrate that our method outperforms competing approaches in sparse approximation and unsupervised Wasserstein distance learning on several word-document and single-cell RNA-sequencing datasets. In addition, integrating our method into HGCN enhances performance in link prediction and node classification tasks.

Tree-Wasserstein Distance for High Dimensional Data with a Latent Feature Hierarchy

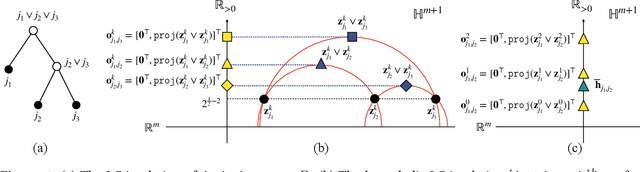
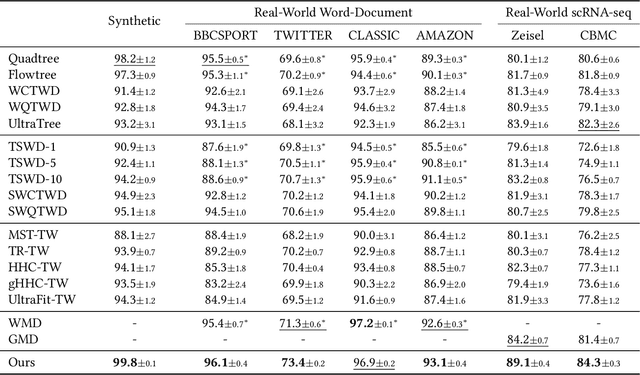
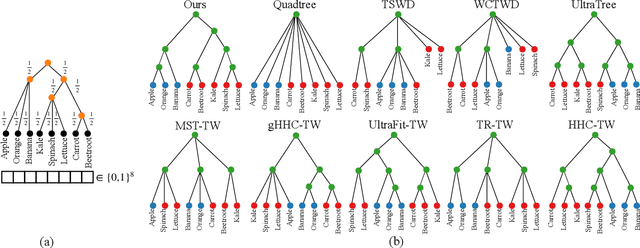
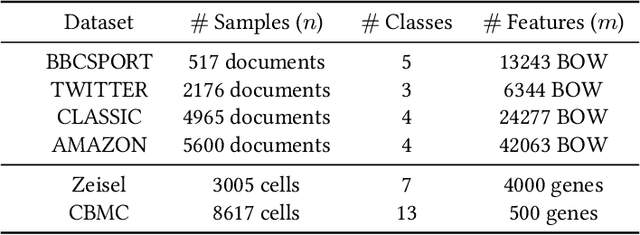
Finding meaningful distances between high-dimensional data samples is an important scientific task. To this end, we propose a new tree-Wasserstein distance (TWD) for high-dimensional data with two key aspects. First, our TWD is specifically designed for data with a latent feature hierarchy, i.e., the features lie in a hierarchical space, in contrast to the usual focus on embedding samples in hyperbolic space. Second, while the conventional use of TWD is to speed up the computation of the Wasserstein distance, we use its inherent tree as a means to learn the latent feature hierarchy. The key idea of our method is to embed the features into a multi-scale hyperbolic space using diffusion geometry and then present a new tree decoding method by establishing analogies between the hyperbolic embedding and trees. We show that our TWD computed based on data observations provably recovers the TWD defined with the latent feature hierarchy and that its computation is efficient and scalable. We showcase the usefulness of the proposed TWD in applications to word-document and single-cell RNA-sequencing datasets, demonstrating its advantages over existing TWDs and methods based on pre-trained models.

Domain Adaptation for DoA Estimation in Multipath Channels with Interferences

We consider the problem of estimating the direction-of-arrival (DoA) of a desired source located in a known region of interest in the presence of interfering sources and multipath. We propose an approach that precedes the DoA estimation and relies on generating a set of reference steering vectors. The steering vectors' generative model is a free space model, which is beneficial for many DoA estimation algorithms. The set of reference steering vectors is then used to compute a function that maps the received signals from the adverse environment to a reference domain free from interfering sources and multipath. We show theoretically and empirically that the proposed map, which is analogous to domain adaption, improves DoA estimation by mitigating interference and multipath effects. Specifically, we demonstrate a substantial improvement in accuracy when the proposed approach is applied before three commonly used beamformers: the delay-and-sum (DS), the minimum variance distortionless response (MVDR), and the Multiple Signal Classification (MUSIC).

On Learning what to Learn: heterogeneous observations of dynamics and establishing (possibly causal) relations among them

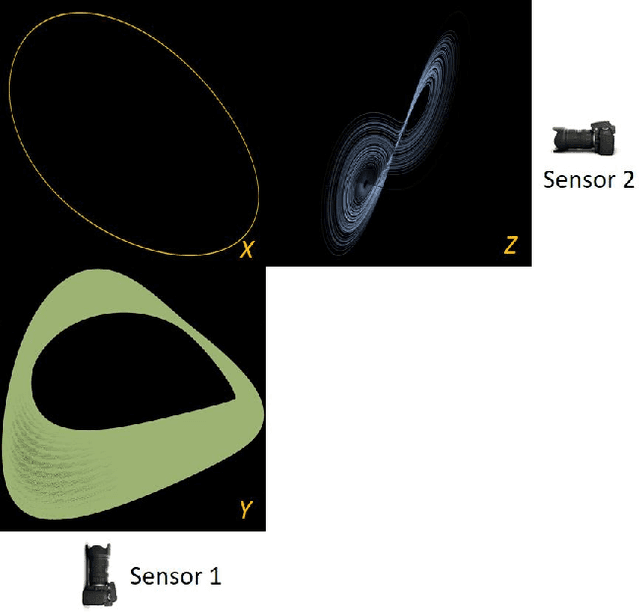
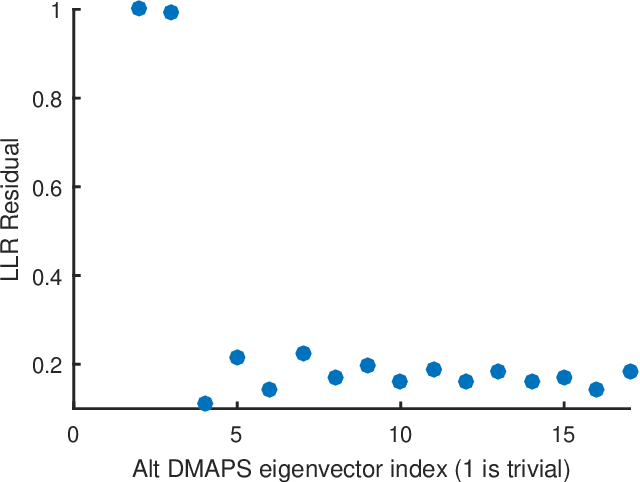
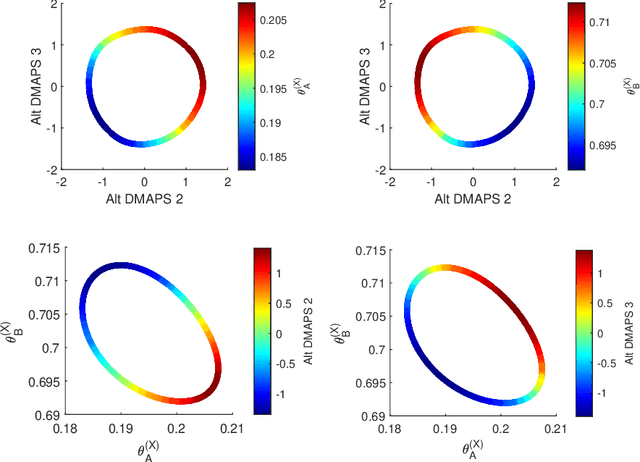
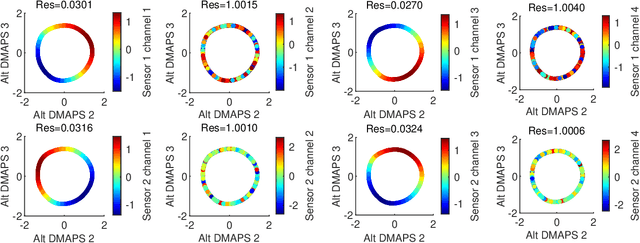
Before we attempt to learn a function between two (sets of) observables of a physical process, we must first decide what the inputs and what the outputs of the desired function are going to be. Here we demonstrate two distinct, data-driven ways of initially deciding ``the right quantities'' to relate through such a function, and then proceed to learn it. This is accomplished by processing multiple simultaneous heterogeneous data streams (ensembles of time series) from observations of a physical system: multiple observation processes of the system. We thus determine (a) what subsets of observables are common between the observation processes (and therefore observable from each other, relatable through a function); and (b) what information is unrelated to these common observables, and therefore particular to each observation process, and not contributing to the desired function. Any data-driven function approximation technique can subsequently be used to learn the input-output relation, from k-nearest neighbors and Geometric Harmonics to Gaussian Processes and Neural Networks. Two particular ``twists'' of the approach are discussed. The first has to do with the identifiability of particular quantities of interest from the measurements. We now construct mappings from a single set of observations of one process to entire level sets of measurements of the process, consistent with this single set. The second attempts to relate our framework to a form of causality: if one of the observation processes measures ``now'', while the second observation process measures ``in the future'', the function to be learned among what is common across observation processes constitutes a dynamical model for the system evolution.

Equivariant Machine Learning on Graphs with Nonlinear Spectral Filters

Equivariant machine learning is an approach for designing deep learning models that respect the symmetries of the problem, with the aim of reducing model complexity and improving generalization. In this paper, we focus on an extension of shift equivariance, which is the basis of convolution networks on images, to general graphs. Unlike images, graphs do not have a natural notion of domain translation. Therefore, we consider the graph functional shifts as the symmetry group: the unitary operators that commute with the graph shift operator. Notably, such symmetries operate in the signal space rather than directly in the spatial space. We remark that each linear filter layer of a standard spectral graph neural network (GNN) commutes with graph functional shifts, but the activation function breaks this symmetry. Instead, we propose nonlinear spectral filters (NLSFs) that are fully equivariant to graph functional shifts and show that they have universal approximation properties. The proposed NLSFs are based on a new form of spectral domain that is transferable between graphs. We demonstrate the superior performance of NLSFs over existing spectral GNNs in node and graph classification benchmarks.

Landmark Alternating Diffusion

Alternating Diffusion (AD) is a commonly applied diffusion-based sensor fusion algorithm. While it has been successfully applied to various problems, its computational burden remains a limitation. Inspired by the landmark diffusion idea considered in the Robust and Scalable Embedding via Landmark Diffusion (ROSELAND), we propose a variation of AD, called Landmark AD (LAD), which captures the essence of AD while offering superior computational efficiency. We provide a series of theoretical analyses of LAD under the manifold setup and apply it to the automatic sleep stage annotation problem with two electroencephalogram channels to demonstrate its application.

Riemannian Covariance Fitting for Direction-of-Arrival Estimation

Covariance fitting (CF) is a comprehensive approach for direction of arrival (DoA) estimation, consolidating many common solutions. Standard practice is to use Euclidean criteria for CF, disregarding the intrinsic Hermitian positive-definite (HPD) geometry of the spatial covariance matrices. We assert that this oversight leads to inherent limitations. In this paper, as a remedy, we present a comprehensive study of the use of various Riemannian metrics of HPD matrices in CF. We focus on the advantages of the Affine-Invariant (AI) and the Log-Euclidean (LE) Riemannian metrics. Consequently, we propose a new practical beamformer based on the LE metric and derive analytically its spatial characteristics, such as the beamwidth and sidelobe attenuation, under noisy conditions. Comparing these features to classical beamformers shows significant advantage. In addition, we demonstrate, both theoretically and experimentally, the LE beamformer's robustness in scenarios with small sample sizes and in the presence of noise, interference, and multipath channels.

The Expected Loss of Preconditioned Langevin Dynamics Reveals the Hessian Rank

Langevin dynamics (LD) is widely used for sampling from distributions and for optimization. In this work, we derive a closed-form expression for the expected loss of preconditioned LD near stationary points of the objective function. We use the fact that at the vicinity of such points, LD reduces to an Ornstein-Uhlenbeck process, which is amenable to convenient mathematical treatment. Our analysis reveals that when the preconditioning matrix satisfies a particular relation with respect to the noise covariance, LD's expected loss becomes proportional to the rank of the objective's Hessian. We illustrate the applicability of this result in the context of neural networks, where the Hessian rank has been shown to capture the complexity of the predictor function but is usually computationally hard to probe. Finally, we use our analysis to compare SGD-like and Adam-like preconditioners and identify the regimes under which each of them leads to a lower expected loss.