Hierarchical Uncertainty Exploration via Feedforward Posterior Trees

When solving ill-posed inverse problems, one often desires to explore the space of potential solutions rather than be presented with a single plausible reconstruction. Valuable insights into these feasible solutions and their associated probabilities are embedded in the posterior distribution. However, when confronted with data of high dimensionality (such as images), visualizing this distribution becomes a formidable challenge, necessitating the application of effective summarization techniques before user examination. In this work, we introduce a new approach for visualizing posteriors across multiple levels of granularity using tree-valued predictions. Our method predicts a tree-valued hierarchical summarization of the posterior distribution for any input measurement, in a single forward pass of a neural network. We showcase the efficacy of our approach across diverse datasets and image restoration challenges, highlighting its prowess in uncertainty quantification and visualization. Our findings reveal that our method performs comparably to a baseline that hierarchically clusters samples from a diffusion-based posterior sampler, yet achieves this with orders of magnitude greater speed.

The Expected Loss of Preconditioned Langevin Dynamics Reveals the Hessian Rank

Langevin dynamics (LD) is widely used for sampling from distributions and for optimization. In this work, we derive a closed-form expression for the expected loss of preconditioned LD near stationary points of the objective function. We use the fact that at the vicinity of such points, LD reduces to an Ornstein-Uhlenbeck process, which is amenable to convenient mathematical treatment. Our analysis reveals that when the preconditioning matrix satisfies a particular relation with respect to the noise covariance, LD's expected loss becomes proportional to the rank of the objective's Hessian. We illustrate the applicability of this result in the context of neural networks, where the Hessian rank has been shown to capture the complexity of the predictor function but is usually computationally hard to probe. Finally, we use our analysis to compare SGD-like and Adam-like preconditioners and identify the regimes under which each of them leads to a lower expected loss.

The Implicit Bias of Minima Stability in Multivariate Shallow ReLU Networks

We study the type of solutions to which stochastic gradient descent converges when used to train a single hidden-layer multivariate ReLU network with the quadratic loss. Our results are based on a dynamical stability analysis. In the univariate case, it was shown that linearly stable minima correspond to network functions (predictors), whose second derivative has a bounded weighted $L^1$ norm. Notably, the bound gets smaller as the step size increases, implying that training with a large step size leads to `smoother' predictors. Here we generalize this result to the multivariate case, showing that a similar result applies to the Laplacian of the predictor. We demonstrate the tightness of our bound on the MNIST dataset, and show that it accurately captures the behavior of the solutions as a function of the step size. Additionally, we prove a depth separation result on the approximation power of ReLU networks corresponding to stable minima of the loss. Specifically, although shallow ReLU networks are universal approximators, we prove that stable shallow networks are not. Namely, there is a function that cannot be well-approximated by stable single hidden-layer ReLU networks trained with a non-vanishing step size. This is while the same function can be realized as a stable two hidden-layer ReLU network. Finally, we prove that if a function is sufficiently smooth (in a Sobolev sense) then it can be approximated arbitrarily well using shallow ReLU networks that correspond to stable solutions of gradient descent.

Exact Mean Square Linear Stability Analysis for SGD

The dynamical stability of optimization methods at the vicinity of minima of the loss has recently attracted significant attention. For gradient descent (GD), stable convergence is possible only to minima that are sufficiently flat w.r.t. the step size, and those have been linked with favorable properties of the trained model. However, while the stability threshold of GD is well-known, to date, no explicit expression has been derived for the exact threshold of stochastic GD (SGD). In this paper, we derive such a closed-form expression. Specifically, we provide an explicit condition on the step size $\eta$ that is both necessary and sufficient for the stability of SGD in the mean square sense. Our analysis sheds light on the precise role of the batch size $B$. Particularly, we show that the stability threshold is a monotonically non-decreasing function of the batch size, which means that reducing the batch size can only hurt stability. Furthermore, we show that SGD's stability threshold is equivalent to that of a process which takes in each iteration a full batch gradient step w.p. $1-p$, and a single sample gradient step w.p. $p$, where $p \approx 1/B $. This indicates that even with moderate batch sizes, SGD's stability threshold is very close to that of GD's. Finally, we prove simple necessary conditions for stability, which depend on the batch size, and are easier to compute than the precise threshold. We demonstrate our theoretical findings through experiments on the MNIST dataset.

Discovering Interpretable Directions in the Semantic Latent Space of Diffusion Models

Denoising Diffusion Models (DDMs) have emerged as a strong competitor to Generative Adversarial Networks (GANs). However, despite their widespread use in image synthesis and editing applications, their latent space is still not as well understood. Recently, a semantic latent space for DDMs, coined `$h$-space', was shown to facilitate semantic image editing in a way reminiscent of GANs. The $h$-space is comprised of the bottleneck activations in the DDM's denoiser across all timesteps of the diffusion process. In this paper, we explore the properties of h-space and propose several novel methods for finding meaningful semantic directions within it. We start by studying unsupervised methods for revealing interpretable semantic directions in pretrained DDMs. Specifically, we show that global latent directions emerge as the principal components in the latent space. Additionally, we provide a novel method for discovering image-specific semantic directions by spectral analysis of the Jacobian of the denoiser w.r.t. the latent code. Next, we extend the analysis by finding directions in a supervised fashion in unconditional DDMs. We demonstrate how such directions can be found by relying on either a labeled data set of real images or by annotating generated samples with a domain-specific attribute classifier. We further show how to semantically disentangle the found direction by simple linear projection. Our approaches are applicable without requiring any architectural modifications, text-based guidance, CLIP-based optimization, or model fine-tuning.

Spectral Discovery of Jointly Smooth Features for Multimodal Data

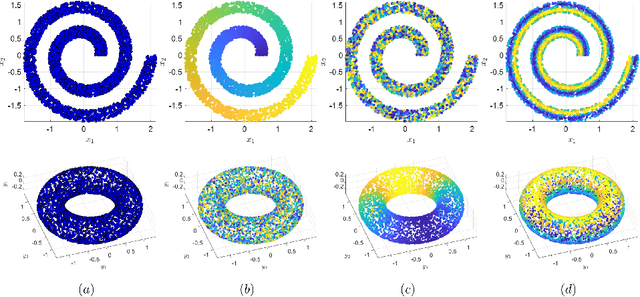
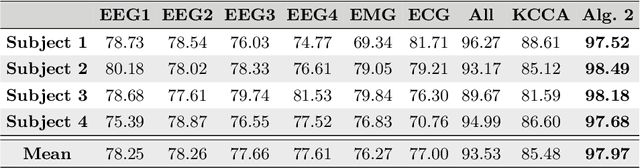
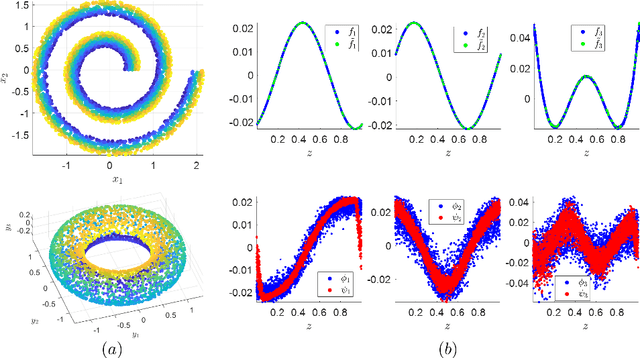
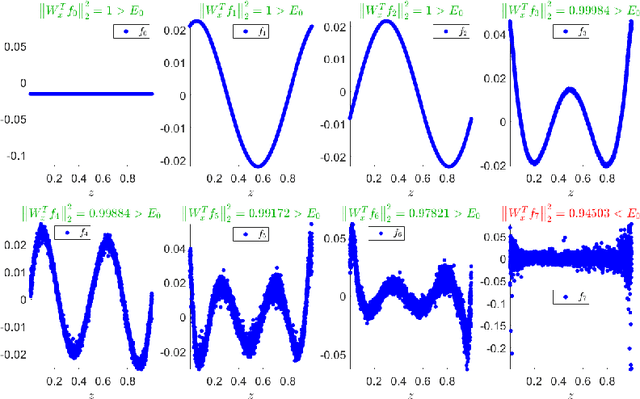
In this paper, we propose a spectral method for deriving functions that are jointly smooth on multiple observed manifolds. Our method is unsupervised and primarily consists of two steps. First, using kernels, we obtain a subspace spanning smooth functions on each manifold. Then, we apply a spectral method to the obtained subspaces and discover functions that are jointly smooth on all manifolds. We show analytically that our method is guaranteed to provide a set of orthogonal functions that are as jointly smooth as possible, ordered from the smoothest to the least smooth. In addition, we show that the proposed method can be efficiently extended to unseen data using the Nystr\"{o}m method. We demonstrate the proposed method on both simulated and real measured data and compare the results to nonlinear variants of the seminal Canonical Correlation Analysis (CCA). Particularly, we show superior results for sleep stage identification. In addition, we show how the proposed method can be leveraged for finding minimal realizations of parameter spaces of nonlinear dynamical systems.

Unique Properties of Wide Minima in Deep Networks

It is well known that (stochastic) gradient descent has an implicit bias towards wide minima. In deep neural network training, this mechanism serves to screen out minima. However, the precise effect that this has on the trained network is not yet fully understood. In this paper, we characterize the wide minima in linear neural networks trained with a quadratic loss. First, we show that linear ResNets with zero initialization necessarily converge to the widest of all minima. We then prove that these minima correspond to nearly balanced networks whereby the gain from the input to any intermediate representation does not change drastically from one layer to the next. Finally, we show that consecutive layers in wide minima solutions are coupled. That is, one of the left singular vectors of each weight matrix, equals one of the right singular vectors of the next matrix. This forms a distinct path from input to output, that, as we show, is dedicated to the signal that experiences the largest gain end-to-end. Experiments indicate that these properties are characteristic of both linear and nonlinear models trained in practice.